一种适用于ATT武器系统的目标跟踪算法

苏 萌，杨赪石，李建辰，王明洲，康文钰

(1.中国船舶重工集团公司第七○五研究所，陕西西安 710075;2.水下信息与控制重点实验室，陕西 西安 710075）

一种适用于ATT武器系统的目标跟踪算法

苏 萌1，2，杨赪石1，2，李建辰1，2，王明洲1，2，康文钰1

(1.中国船舶重工集团公司第七○五研究所，陕西西安 710075;2.水下信息与控制重点实验室，陕西 西安 710075）

提出一种基于单站纯方位的水下高速目标跟踪算法。该算法在快速估计出目标航向的基础上，利用目标先验速度信息解算出其他目标运动要素。该算法收敛速度快，对观测平台机动要求低且具有一定精度，能满足反鱼雷鱼雷武器系统的要求。

目标跟踪;反鱼雷鱼雷武器系统;算法

0 引言

现代反舰鱼雷命中精度高，毁伤威力大，对舰艇的威胁越来越大，因此各国海军都开始不断升级和改进原有的鱼雷防御系统，力图使舰艇鱼雷防御能力得到显著提高。其中以反鱼雷鱼雷 (ATT）为对抗武器的硬杀伤性武器正成为许多国家集中研究的领域。

反鱼雷鱼雷作为积极、主动搜寻并拦击来袭鱼雷的硬杀伤性武器，是鱼雷防御系统中最后和最关键的防线。反鱼雷鱼雷能否有效拦截来袭鱼雷的先决条件是反鱼雷鱼雷武器系统能否在足够远的距离上可靠地探测和识别来袭鱼雷攻击、发出鱼雷报警并对来袭鱼雷进行跟踪定位。

现代反舰鱼雷攻击段速度一般可达到50 kn左右。目前各国在役舰艇配备的鱼雷探测与报警系统主要有舰壳声呐、拖曳线列阵声呐和专用鱼雷报警声呐。对于鱼雷这种水下高速小目标，一般在距离本舰5 km内时才能提供较为有效的方位信息，留给反鱼雷鱼雷武器系统的反应时间非常短，一般不会超过3 min。来袭反舰鱼雷 (下文统称为目标）跟踪问题是一个典型的单站纯方位问题，一般要求观测站做较大幅度的转向机动来保证系统可观测，这对本舰来讲有时是无法完成的。

因此，适用于反鱼雷鱼雷武器系统的目标跟踪方法应具有以下特征:

1）收敛速度快，满足反鱼雷鱼雷武器系统反应时间短的要求;

2）对观测平台的机动要求低;

3）具有一定精度，满足反鱼雷鱼雷射击参数的要求。

本文从单静止观测站入手，提出一种基于单站纯方位的水下高速目标跟踪算法。该算法收敛速度快，对观测平台机动要求低且具有一定精度，能够满足反鱼雷鱼雷武器系统的要求。

1 数学模型

一般来讲，反舰鱼雷航行至攻击段时，深度维持在10 m左右，速度为高速制，且不会有较大机动。为研究方便且不失一般性，只考虑其横向平面内的二维运动情形，并假定目标做匀速直线运动。依此建立目标在观测站地理坐标系中的态势图如图1所示，x轴指向正东，y轴指向正北，观测站位于坐标系原点，目标在XY平面内做匀速直线运动。

图1 观测站与目标二维态势图Fig.1 Two-dimensional chart of observing station and target

显然，(D0，Cm，Vm，β0）可以唯一地确定目标的运动轨迹。各参数定义如下:目标初始距离D0为观测站到目标之间的初始直线距离;目标航向Cm为正北到目标航向线之间的夹角，顺时针计算;目标速度Vm为目标相对于大地运动速度量的大小;目标方位角β为正北到观测站与目标连线之间的夹角，顺时针计算。

(Vmx，Vmy，xm0，ym0）也可唯一确定目标的运动轨迹。目标跟踪的过程就是解出向量(D0，Cm，Vm，β0）或(Vmx，Vmy，xm0，ym0）的过程。目标方位角与上述向量之间的关系为

当 βj(j=0，1，2，…，k）已知时，利用式(2）便可以形成关于(Vmx，Vmy，D0）的非线性方程组。

2 算法描述

目标跟踪问题在数学上是一个求解目标运动要素的过程。众所周知，单静止站纯方位目标跟踪系统是不可观测的，也就是说仅依靠方位角序列信息无法将目标的运动要素全部解出。

在对单静止站纯方位系统的具体分析过程中，发现可以通过某些方法求解出目标的部分要素组合式，在此基础上结合某些先验信息，便有可能最大精度地求解出其他目标的运动要素来。本算法旨在通过某些间接的方法估计出目标航向后，利用目标先验速度信息，计算出具有一定精度的其他目标运动要素 (比如初距）来。

目标方位角变化率不为0时，任取0≤i＜j≤k，有

2.1 最小二乘法

下面基于最小二乘滤波，给出一种适用于单静止站纯方位系统的目标跟踪算法。

2.2 扩展卡尔曼滤波法

与最小二乘滤波相比，卡尔曼滤波能定量识别各种信息的质量，自动确定对这些信息的利用程度，具有一定智能;而且卡尔曼滤波具有初值遗忘的特性，在目标航向发生改变时，可以自动进行跟踪。由于卡尔曼滤波具有这些最小二乘滤波所不具备优点，下面采用卡尔曼滤波法对(Vmx/D0，Vmy/D0）进行估计。

在纯方位观测条件下，目标做匀速直线运动，式(10）可改写为:

3 仿真分析

3.1 目标航向仿真及分析

假定态势如下:观测站位于坐标原点，来袭鱼雷初始位置坐标 (1 000，3 000），速度为25 m/s(约 49 kn），其中 Vmx为 10 m/s，Vmy为 23 m/s，信息数据率为1 s，方位角量测值方差为1°。

假设系统的激励噪声和量测噪声均为互不相关的零均值高斯白噪声，使用第2.1节所述最小二乘法，对目标航向进行估计。随机抽取3次仿真实验结果，可以看到，系统在100 s左右均收敛，如图2所示。

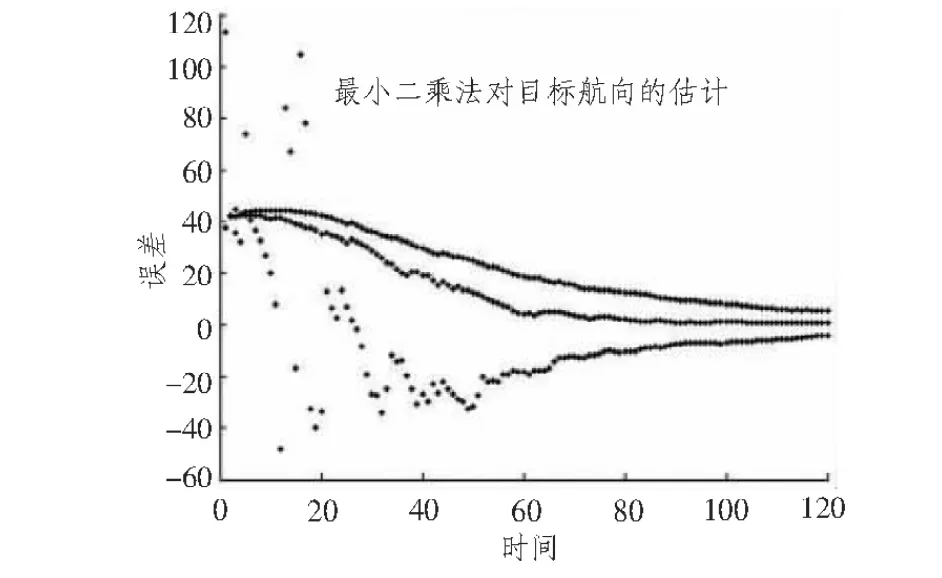
图2 最小二乘法对目标航向的估计效果图Fig.2 Least squaresmethod for the estimated effect of the target course

使用第2.2节所述扩展卡尔曼滤波法，对目标航向进行估计。随机抽取3次仿真实验结果，可以看到，系统在60 s左右均收敛，如图3所示。

观察以上2组仿真结果可知:卡尔曼滤波法比最小二乘法收敛速度更快，收敛精度更高。

3.2 目标初距仿真及分析

图3 EKF法对目标航向的估计效果图Fig.3 EKFmethod for the estimated effect of the target course

继续使用第3.1节所述仿真条件，对目标初距进行实时估计。记目标先验速度为V先，目标速度为Vm，误差为δ，有

假定目标速度为49 kn，误差δ服从均值为0，方差为1的正态分布，即来袭鱼雷速度在47～51 kn之间，随机抽取1次仿真实验结果，如图4所示。

图4 EKF法对目标初距的估计效果图 (δ～ (0，1））Fig.4 EKFmethod for the estimated effect of the target initial distance(δ～ (0，1））

假定误差δ服从均值为0，方差为2.5的正态分布，即目标速度在44～54 kn之间，随机抽取1次仿真实验结果，如图5所示。

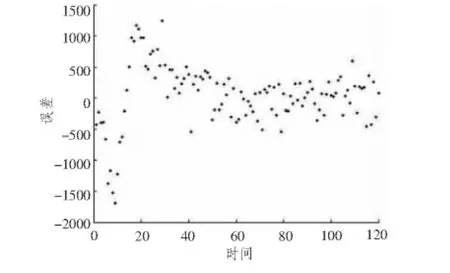
图5 EKF法对目标初距的估计效果图 (δ～ (0，2.5））Fig.5 EKFmethod for the estimated effect of the target initial distance(δ～ (0，2.5））

图4中初距收敛后误差稳定散布在约150 m以内，图5中稳定散布在约350 m以内。观察以上2组仿真结果可知，当先验速度误差增大时，初距误差也随之增大。

式(12）代入式(9），有

由式(13）可知，目标初距估计值的误差约等于目标初距与速度误差比的乘积。由于本文采用了先估计航向，再确定计算初距的方法，所以这一部分误差是无法消除的，仿真结果也反映了这一点。

进一步，在本舰艇可以做有效机动的情况下，研究如何将先验速度信息引入系统方程显得极具价值，在引入速度相关的被估计量后，就可以通过滤波减小速度误差，获得更加精准的距离要素。另一方面，反舰鱼雷处于攻击段时速度一般会稳定在某一速制 (一般为高速制），误差不会超过1～2 kn，通过某些手段(参数辨识或人工判定等）识别出来袭鱼雷的类型、速制来，也同样可以获得足够精准的距离要素。

4 结语

随着舰载计算机硬件的飞速发展，多套算法并行处理成为了可能。在使用某些特定算法先行估计出具有一定精度的要素后，可以作为其他目标跟踪算法的初始信息，从而在数据量有限的情况下，最大可能、最大精度地实现对目标的快速跟踪。本文中提出的目标跟踪算法便非常适合作为某些初值敏感算法的前端算法。

［1］陈春玉.反鱼雷技术［M］.北京:国防工业出版社，2006.CHEN Chun-yu.Anti-torpedo technology［M］.Beijing:National Defence Industry Press.

［2］董志荣.纯方位TMA案例分析［J］.情报指挥控制系统与仿真技术，2005(8）:4 －6，11.

［3］秦永元.卡尔曼滤波与组合导航原理［M］.西安:西北工业大学出版社，1998.

［4］刘忠，邓聚龙，等.速运动观测站纯方位系统的可观测性［J］.火力与指挥控制，2004，10.

［5］BLACKMAN S，POPOLIR.Design and analysis ofmodern tracking systems［Z］.Artech House，Norwood，1999.

［6］ZHOU D，MU C，XUW.Adaptive two-step filter with application to bearings-only measurement problem［J］.Journat of Guidance，Control and Dynamics，1999，22(5）:726 －728.

A kind of target tracking algorithm for ATT weapon system

SU Meng1，2，YANG Cheng-shi1，2，LIJian-chen1，2，WANG Ming-zhou1，2，KANGWen-yu1
(1.The 705 Research Institute of CSIC，Xi'an 710075，China;2.Science and Technology on Underwater Information and Control Laboratory，Xi'an 710075，China）

In this paper，a kind of bearing-only tracking algorithm was proposed for high-speed underwater target.The algorithm estimated target course firstly，and then priori velocity was used to solve the othermotion elements.This algorithm convergence fast，don't need much observing platform motorizing，can meet the requirements of the anti-torpedo weapon system.

target tracking;ATT weapon system;algorithm

E925.23

A

1672－7649(2013）03－0082－04

10.3404/j.issn.1672－7649.2013.03.018

2012－10－29;

2012－12－07

苏萌(1985－），男，硕士研究生，主要研究方向为鱼雷总体技术。