近岸较大区域波浪数值模型的比较

武国相, 田克峰, 相昌盛, 邬德宇

(1. 中国海洋大学 工程学院, 山东 青岛 266100; 2. 中交天津港湾工程设计院有限公司, 天津 300461; 3.中交天航滨海环保浚航工程有限公司, 天津 300450)

近岸较大区域波浪数值模型的比较

武国相1, 田克峰2, 相昌盛1, 邬德宇3

(1. 中国海洋大学 工程学院, 山东 青岛 266100; 2. 中交天津港湾工程设计院有限公司, 天津 300461; 3.中交天航滨海环保浚航工程有限公司, 天津 300450)

将适用于近岸较大区域波浪传播变形的三种模型, 即基于抛物型缓坡方程的不规则波模型、引入浅水波浪谱TMA谱的SWAN(simulating waves nearshore)模型以及采用默认JONSWAP谱的SWAN模型应用于特拉华大学(University of Delaware)圆形浅滩实验进行比较。结果显示, 抛物型缓坡方程和SWAN的模拟结果与实验所测数据符合都比较好; SWAN在非线性作用较强的浅滩中心及靠后部效果更佳, 而抛物型缓坡方程由于没有考虑非线性作用, 模拟得到的最大波高较实测值偏高, 且波高变化较为剧烈。

抛物型缓坡方程; SWAN(simulating waves nearshore); 圆形浅滩; 不规则波; TMA谱

对于自外海到近岸较大区域的波浪场计算, 目前一般采用抛物近似型缓坡方程或者基于能量守恒的相位平均波浪模型。抛物型缓坡方程属于规则波模型, 如果忽略波与波之间的相互作用, 采用线性叠加法则可以使之用于不规则波的计算; SWAN (simulating waves nearshore)[1]是基于动谱平衡方程的第三代波浪模型, 全面地考虑了波浪浅化、折射、绕射[2]、底摩擦、破碎、白浪、风能输入及波浪非线性效应。本文将适用于浅水地区的 TMA谱[3]引入SWAN, 与采用默认JONSWAP谱的SWAN以及抛物型缓坡方程应用于特拉华大学(University of Delaware)圆形浅滩实验, 并与实验的实测结果进行对比和分析, 得到了具有一定工程应用价值的结论。

1 模型介绍

1.1 抛物型缓坡方程

本文采用的抛物型缓坡方程为:

式中,C为波速,Cg为波群速度,φ为速度势函数,k为波数。

方程采用Crank-Nicholson格式进行离散求解。对于不规则波, 本文忽略波与波之间的非线性相互作用, 采取线性叠加法[4-5]进行计算。根据随机波浪理论, 不规则波可视为由不同方向、不同频率的组成波叠加而成。波面高度可表示为:

式中:ξ为波面高度,amn为组成波振幅,fm为组成波频率,km为组成波波数,θn为组成波的波向,εmn为随机初相位, 服从(0,2π)区间的均匀分布。

波浪能量在频率和方向上的分布可由波浪方向谱S(f,θ)表示:

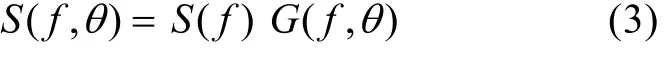
式中:S(f)为频率谱,G(f,θ)为方向分布函数。

不规则波有效波高和波谱的关系为:Hs≈ 4.0,式中:m0是波谱的零阶矩, 定义为:

在不规则波模型中, 采用频率方向对应法对波浪谱进行离散, 组成波振幅amn可由离散化的波谱确, 将每一组成波计入缓坡方程进行计算, 最终(x,y)处合成的波高值为:

考虑到浅水波浪破碎[6], 计算出各个点的波高后, 与当地水深决定的最大(破碎)波高对比, 如果大于当地水深的最大(破碎)波高, 则波高按照当地水深的最大波高取值, 而后进入下一步的计算。

1.2 SWAN模型

SWAN[1]模型是一种基于能量守恒原理的波浪谱模型, 各种物理过程(例如风生浪作用、底摩擦耗散、波浪破碎、波-波相互作用等等)用不同的源函数表示, 有效地简化了波浪场的动力学计算过程, 同时它对空间和时间步长没有苛刻的要求, 可适用于较大区域和长时间尺度的计算。

SWAN模型是以二维动谱密度表示随机波。其中动谱密度N(σ,θ)为能谱密度E(σ,θ)与相对频率σ的比值。在直角坐标系下, 动谱平衡方程表示为

其中N为波浪作用谱,cx,cy,cσ,cθ分别是x,y,σ,θ方向的空间传播速度。左边第一项为N随时间的变化率; 第二、三项代表N作用在地理空间的传播; 第四项是N在相对频率空间σ的变化, 主要是由水深和流速的变化产生; 第五项代表由于水深和流而引起的折射。这几种传播速度的具体表达式可用线性波浪理论获得。该方程右侧S为波作用密度的源项,该项是由风能输入、波浪耗散、波与波之间非线性、波浪绕射相互作用四个部分组成。

2 圆形浅滩实验

2.1 实验布置

模型采用 Chawla等[4]在特拉华大学所做的圆形浅滩实验进行验证分析。如图 1 所示, 水池长18 m, 宽18.2 m, 圆形浅滩以外部分水深相同。沿浅滩周围的 1个纵断面(A-A′)、6个横断面(B-B′, C-C′, D-D′, E-E′, F-F′, G-G′)采集实验数据。浅滩中心位于x＝5 m,y＝8.98 m处, 半径2.57 m, 水深可表示为:

其中h0为浅滩以外的水深,h0＝0.4 m, 浅滩顶部的水深为0.03 m。

边界处(x=0)入射的波浪谱采用TMA谱:

图1 实验地形及实验数据采集位置Fig. 1 Experiment bathymetry and data locations

式中α是Phillips常数,fm是谱峰频率,γ是谱峰升高因子, 取γ＝10,σs是峰形参数,φ(f,h)是包含水深影响的无因次函数。φ(f,h)可近似表示为

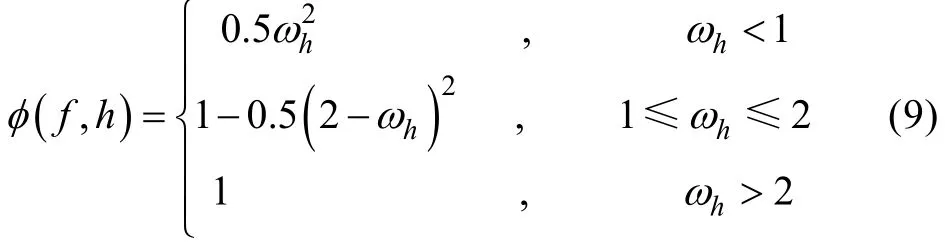
式中θ0是入射波向, 取0°,σd是方向分布的标准差,L是级数的项数, 取50。

SWAN中默认采用的方向分布函数为:

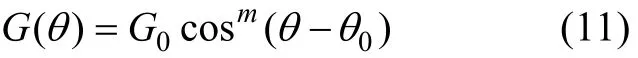
其中,θ0为主入射波向,m取较大值时, 方向分布宽度越窄, 取较小值时, 分布宽度越宽,G0为常数,其值可由下式决定:

对应于Wrapped-normal分布函数中σd＝5,σd＝20, 可分别取m＝120,m＝7(表1), 由下面的图2可看出, 此时两种分布函数基本相同, 计算结果不会因为方向分布函数的不同而受到影响。

取原实验的其中两组, 如表1所示, 其中实验1方向分布宽度较窄、入射波高较小, 实验2方向分布宽度较宽、入射波高较大; 两种情况下中、浅滩上方均发生波浪破碎。

表1 实验入射波浪参数及破碎指标Tab. 1 Incident wave parameters and breaking indexes

2.2 模型设置

实验分三组进行对比, 第一组为修改后的SWAN, 采用TMA频率谱; 第二组采用SWAN默认的 JONSWAP谱; 第三组为抛物型缓坡方程不规则波浪模型。分组情况如表2所示。

第一组实验中, SWAN模型采用笛卡尔坐标系,将计算区域划分为182×180个网格,x,y方向的计算精度均为0.1 m; 将TMA频率谱应用于SWAN, 计算范围1～3 Hz, 采用指数分割法划分数为30。方向谱计算范围为–60°～60°, 计算精度2°; 开启绕射项、三波相互作用和波浪破碎, 关闭风的成长和四波相互作用; 波浪破碎指标取值如表1所示。

第二组中, SWAN采用默认的JONSWAP谱, 其他参数设置同第一组。

第三组抛物型缓坡方程模型中, 频谱采用 TMA谱, 方向谱采用 Wrapped-normal分布函数, 计算范围和计算精度与 SWAN模型中相同, 频谱划分数为30, 方向谱划分数为60。为了便于对比, 波浪破碎指标每组的取值同 SWAN。各组入射波浪的频率谱和方向谱如图2所示。

表2 实验分组情况及其采用的波浪谱Tab. 2 Test groups and wave spectra

图2 频率谱和方向Fig. 2 Frequency spectra and direction spectra

3 实验结果与分析

各组相对波高值(H/H0)(波高计算值与入射波高的比值)如图3～图5所示。

图 3为纵断面 A-A′上的相对波高, 可以看出SWAN和抛物型缓坡方程均能较好地模拟波浪在圆形浅滩地形上的传播与变形。在浅滩的中心及其偏后的部分, 也是波浪非线性作用和波浪破碎作用最强的部分, SWAN的模拟效果比较准确, 尤其是较宽方向分布的情况, 在较窄的方向分布情况下, 模拟的波高最小值有些偏高, 而最大值则稍微偏低些;与之相比, 抛物型缓坡方程的结果相对不太理想,浅滩中心偏前部分计算值较实测值偏低, 中心及偏后部分最大波高的计算值则偏大(实验 1 1.7VS1.4,实验2 1.9VS1.5)。这可能是因为在抛物型缓坡方程中是以规则波线性叠加法模拟不规则波, 没有考虑波波相互作用, 且对于波浪破碎也仅仅是在对应当地水深和破碎指数在波高上进行线性修正, 而波浪破碎是非线性作用非常强的过程, 耗散能量非常大,故浅滩中后部模拟值较实测值高。仅就SWAN来讲,对于方向分布较宽的实验 1的模拟结果比方向分布较窄的实验 2模拟结果更为准确, 这一点 Hu和Ding[8]也曾论述过; 而TMA谱的计算结果较SWAN默认的 JONSWAP谱略微偏小, 原因是本实验中TMA谱中的水深因子φ(f,h)对波浪谱的形状影响很小。

图3 A-A′纵断面的相对波高Fig. 3 Relative wave heights along section A-A′

图4 实验1各横断面的相对波高Fig. 4 Relative wave heights along section B-B′ to G-G′ in experiment 1

图5 实验2各横断面的相对波高Fig. 5 Relative wave heights along section B-B′ to G-G′ in experiment 2

图4和图5是六个横断面上的相对波高, 对比实验1、实验2可以看出, 方向分布宽度越大, 浅滩后波高分布越平缓, 在刚到达浅滩的G-G′, F-F′断面以及浅滩后的三个断面(B-B′, C-C′, D-D′)处SWAN和抛物型缓坡方程的模拟结果都非常好; SWAN的结果在实验 1 的 F-F′断面和实验 2 的 E-E′断面偏小;在 E-E′断面, 抛物型缓坡方程得到的波高分布更为集中, 波高最大值较实测偏大(实验1 1.4VS1.4 实验2 2.0VS1.4)。各个横断面的波高分布总体来说, 抛物型缓坡方程和SWAN的计算结果都还是令人满意的,抛物型缓坡方程由于没有考虑波浪的非线性作用,在浅滩中后部的准确度还有待改进。

4 结论

(1)本文针对 Chawla等在特拉华大学所做的圆形浅滩实验, 分别采用添加TMA谱的SWAN、默认的SWAN和抛物型缓坡方程模拟了波浪在浅滩地形上的传播变形并与实测数据对比, 结果显示这几种模型均与实验结果符合较好, 其中在波浪破碎较为剧烈的浅滩中心及靠后的地方, 考虑了波浪非线性作用和较合理的波浪破碎作用的SWAN模型更加准确, 对于近岸波浪场的计算, SWAN和抛物型缓坡方程均能满足工程应用的需要。(2)无论是选用TMA谱,还是JONSWAP谱对本实验的计算结果均影响不大。

[1] Booij N, Holthuijsen L H, Ris R C. The “SWAN” wave model for shallow water[J]. Coastal Engineering, 1996, 1: 668-672.

[2] Holthuijsen L H, Herman A, Booij N. Phase-decoupled refraction-diffraction for spectral wave models[J]. Coastal Engineering, 2003,49(4): 291-305.

[3] Bouws E, Gunther H, Rosenthal W, et al. Similarity of the wind wave spectrum in finite depth water[J]. Journal of Geophysical Research, 1985, 90: 975-986.

[4] Chawla A, Okan-Haller H T, Kirby J T. Spectral model for wave transformation and breaking over irregular bathymetry[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1998, 124(4): 189-198.

[5] 陶建华, 韩光. 高阶近似抛物缓坡方程的随机波模型[J]. 中国港湾建设, 2001, 12(6): 20-25.

[6] 陈汉宝, 张福然, 陈阳, 等. 抛物线形缓坡方程波浪数学模型研究[J]. 水道港口, 1999, 6(2): 25-30.

[7] Borgman L E. Directional spectrum estimation for Sxy gages-Technical Report[R]. Vicksburg, MS, USA: CERC Waterways Experiment Station, 1984.

[8] Hu Kelin, Ding Pingxing. Numerical study of wave diffraction effect introduced in the SWAN model[J]. China Ocean Engineering, 2007, 21(3): 495-506.

(本文编辑: 刘珊珊)

Performance comparison of wave models for large coastal areas

WU Guo-xiang1, TIAN Ke-feng2, XIANG Chang-sheng1, WU De-yu3
(1. College of Engineering, Ocean University of China, Qingdao 266100, China; 2. Tianjin Port Engineering Design & Consulting Company Ltd. of China Communications Construction Company, Tianjin 300461, China; 3. China Communications Construction Company Binhai Environmental Channel Dredging Company Ltd., Tianjin 300450, China)

Aug.,31, 2011

parabolic mild slope equation; SWAN(simulating waves nearshore); circular shoal; random wave; TMA spectrum

Random wave model based on approximate parabolic mild slope equation, (simulating waves nearshore) (SWAN) modified for TMA spectrum and SWAN with default JONSWAP spectrum were applied for the circular shoal experiments in the wave basin of University of Delaware. The results all agreed well with the data. SWAN gave better results at the shoal center and behind the shoal. Because nonlinear interaction was ignored in parabolic mild slope equation model, it gave higher maximum value and wave heights varied sharply in space.

TV139.2

A

1000-3096(2013)01-0001-06

2011-08-31;

2012-11-27

国家自然科学基金(50809065)

武国相(1986-), 男, 山东青岛人, 硕士, 从事河口海岸水动力数值研究, E-mail: wuguoxiang9@163.com