MW风力发电机齿轮动态数值计算
沈 健, 路永品, 朱仁胜, 房 震, 韩昕彤
(合肥工业大学 机 械与汽车工程学院,安徽 合 肥 230009)
增速箱是风力发电机中最主要的传动系统,结构紧凑、传动动力大,起到变速、传递能量的作用,它的运行情况直接影响整机的工作性能,而齿轮是其中最重要的传动零件,所以对风力发电机增速齿轮进行动态数值计算是非常必要的。一般风力发电机安装在山区、高原和海岛等风力比较大的地方,工作环境非常恶劣,受各种变化的风力载荷和冲击,而且温度变化比较大,所以对增速箱的各工作性能要求非常高,要求其结构合理,维修周期长,寿命长,能保持良好的工作状态[1-3]。
文献[4]建立了增速箱圆柱齿轮传动三维有限元模型,采用有限元法,求解出正常工作和故障频率情况下的圆柱传动齿轮的应变和等效应力的变化,分析了双圆柱齿轮正常转速下的故障振动特性。文献[5]采用一种较为实用和合理的有限元混合法,对基于斜齿轮啮合线理论获得齿轮理论接触线的每一啮合位置,生成有限元网格模型,对齿轮进行了啮合周期内的准稳态仿真计算。文献[6]通过建立齿轮有限元模型,对齿轮在静态载荷和冲击载荷作用下的动态特性进行了数值计算和分析,并根据风力机的运行情况,研发了风力机的传动试验台,进行数据实验和数值模拟结果对比研究。文献[7]针对某风力发电齿轮箱中齿轮副啮合特性,对其瞬态啮合性能进行了研究,通过对模拟计算结果进行对比分析,得到了在齿轮副啮合过程中各瞬态时刻齿轮各处的应力分布和振动情况,以及随时间推移啮合齿轮各处应力和振动状态的变化情况。文献[8]进行了MW级风力发电机齿轮的参数化建模、接触分析,并与理论公式计算结果进行对比,得出了齿轮强度的设计依据。
本文利用SOLIDWORKS的齿轮插件,建立风力发电机增速箱齿轮对的实体模型,运用ANSYS对其进行动态分析,模拟齿轮转动时的工况,对齿轮对进行数值计算,通过与理论计算值比较,验证了数值计算的准确性。
1 数值计算
1.1 啮合对的建模
本文以二级平行轴上的齿轮为研究对象,平行轴输出端与发电机连接。二级平行轴的输入转速为738r/min,输入转矩为38.7kN·m。通过Geartrax齿轮插件生成风力发电机斜齿轮的三维模型齿轮参数,见表1所列,啮合对实体模型如图1所示。

表1 齿轮参数

图1 斜齿轮啮合配合图
1.2 划分网格
定义齿轮材料的物理参数如下:弹性模量为2.1×1011Pa,泊松比为0.3,摩擦因数为0.2。考虑到计算精度要求、计算齿形的复杂程度以及计算的经济性等因素,本文采用8节点Solid185单元,另外定义Plane42单元作为对线、面划分网格时的分析单元[9]。在划分网格时,精度6级,使用Plane42单元分别对小齿轮的一个端面和齿的一条斜线进行自由网格划分。然后应用Solid185单元对体进行扫描划分,生成较规则的有限元网格。同样,对大齿轮进行网格划分。
1.3 创建接触对
创建接触对之前,分别选择大小齿轮对应啮合的齿面,分别对附在面上的节点创建节点组,2组节点分别命名为CE、TE,完成接触对的创建[10],如图2所示。

图2 所创建的接触对
1.4 施加边界条件和载荷
本文利用接触对实现对从动轮的约束和对主动轮的驱动。其原理是利用接触对在齿轮中心孔轴线上生成一个节点,该节点通过约束方程与内孔面上的节点形成耦合,耦合后可直接在中心节点上施加约束或载荷,中心节点通过约束方程将约束或者载荷传递到内孔面的节点上。
1.5 计算结果分析
3个载荷步下的应力云图如图3~图5所示。

图3 第1载荷步下的应力云图
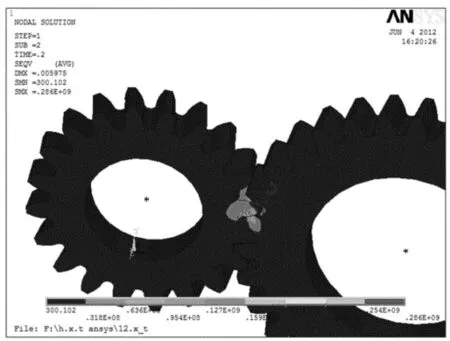
图4 第2载荷步下的应力云图
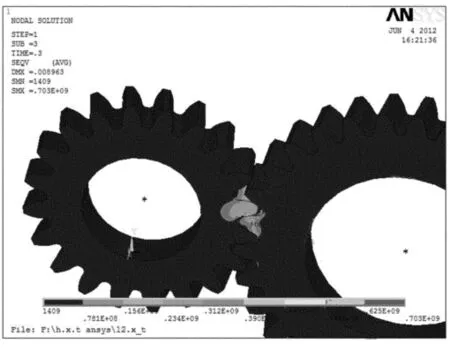
图5 第3载荷步下的应力云图
从图3~图5可以看到,接触应力的大小及应力最大位置随着时间变化而变化。从图5可以看出最大接触应力为703MPa。最大接触应力发生在齿轮的分度圆附近,这是由于齿轮边缘的接触造成了轮齿之间的互相剪切作用,使得在主、从动轮的齿轮边缘处都出现了应力集中现象,接触应力出现最大值。从图5中还可以看出,接触应力沿着齿廓方向的分布规律如下:接触线附近的接触应力最大,往两侧逐渐减小,到齿顶位置基本为0。齿轮的齿根圆角处也产生了较大的应力,齿轮啮合过程中最容易折断,这也是齿轮的主要失效形式之一。因此在设计中要适当增大齿根圆角半径。
2 理论计算及验证
斜齿圆柱齿轮的齿面接触应力按节点处计算,并综合考虑螺旋角的影响。在斜齿轮传动过程中,作用于齿面上的载荷垂直于齿面,为法向载荷。法向载荷可沿齿轮的周向、径向及轴向分解为3个相互垂直的分力,其受力分析图如图6所示。
图6中,β为节圆螺旋角,对于标准斜齿轮则为分度圆螺旋角;βb为基圆螺旋角,αn为法向压力角,对于标准斜齿轮αn=20°;αt为端面压力角;Fn、Ft、Fr、Fa分别为法向力、切向力、径向力、轴向力。
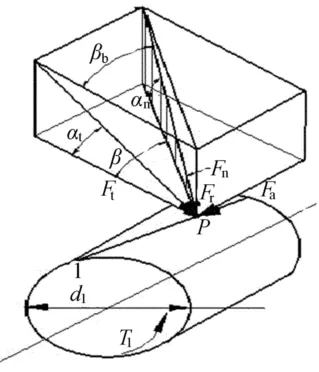
图6 斜齿轮受力分析
斜齿轮接触应力的赫兹公式[11]为:

其中,σ为节圆上的接触应力;ZH为节点区域系数,用来考虑节点处齿面形状对接触应力的影响;ZE为弹性系数,表示弹性模量和柏松比对接触应力的影响;Zε为重合度系数;Zβ为螺旋角系数;K为载荷系数;Ft为端面内分度圆上的切向力;b为齿宽;d2为小齿轮风度圆直径;u为齿轮传动比。
分别计算(1)式中的各个参数,过程如下。
(1)计算节点区域系数ZH。斜齿轮的法向压力角αn即为表1给出的压力角。计算齿轮的端面压力角αt:

计算基圆螺旋角βb:

则节点区域系数为:

(2)计算弹性系数ZE。大小齿轮的材料都是钢,弹性模量为E1=E2=2.06×105N/mm2,泊松比为ν1=ν2=0.3,则
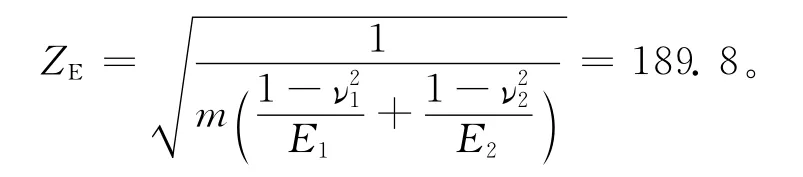
(3)计算重合度系数Zε。斜齿轮的轴面重合度εβ为:
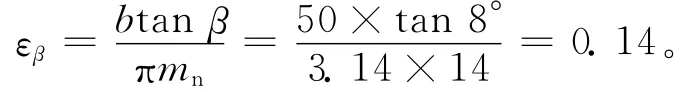
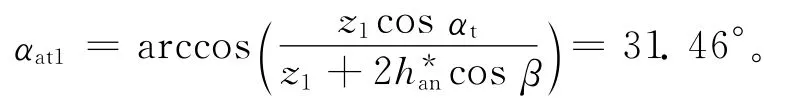
小齿轮的齿顶圆端面压力角αat2为:
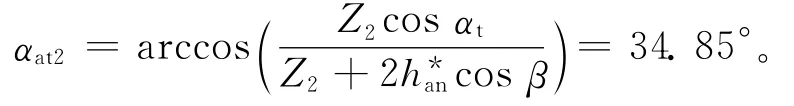
端面重合度εα为:

则斜齿轮的重合度系数Zε为:

(4)计算螺旋角系数Zβ,即
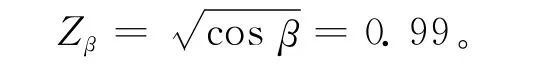
(5)计算切向力Ft,即

(6)计算载荷系数K。KA是考虑由于啮合外部因素引起的的动力过载影响的系数,这种过载取决于原动机和从动机械的特性、质量比、联轴器以及运行状态。风力发电机的原动机要求运行均匀平稳,故选取KA=1.1。动载荷系数KV是用来考虑齿轮副在啮合过程中因啮合误差而引起的内部附加动载荷对齿轮受载的影响。高精度齿轮在良好的安装和对中精度以及合适的润滑条件下,KV为1.0~1.1,本文选择KV=1.01。
齿向载荷分布系数为KHβ,齿宽系数为:

按照齿宽300mm选取,根据文献[11]得KHβ=1.21。由于=670N/mm≥100N/mm,依据文献[11]得齿间载荷分配系数KHα=1。所以,载荷系数K为:

(7)计算齿轮传动比u,即

(8)计算小齿轮分度圆直径d2,即
d2=mz2=14×20=280mm。将以上计算结果带入赫兹公式得斜齿轮接触应力:数值计算的结果为703MPa,与赫兹公式计算的结果相对误差为:


因此,数值计算与赫兹公式的计算结果基本吻合。
3 结束语
本文对风力发电机齿轮进行了动态接触分析,计算得到的接触应力大小为703MPa,与赫兹理论计算结果690MPa基本吻合,说明了分析方法的可靠性;找出了风力发电增速齿轮的最危险部位,即轮齿接触表面的分度圆附近和齿根圆角处,接触表面的分度圆附近容易发生接触疲劳,齿根圆角处容易发生轮齿折断,这与实际工况一致。对风力发电增速箱齿轮进行动态接触有限元分析,掌握其在接触应力作用下的变形和应力情况,为改善风电齿轮轮齿接触状况、提高其承载能力和性能提供了可靠的分析方法。
[1] 张志英,李银凤,刘万琨,等.风能与风力发电技术[M].北京:化学工业出版社,2007:106-107.
[2] 赵志军,刘正士,谢 峰.基于时序分析的齿轮箱故障诊断[J].合肥 工业大 学学 报:自然科 学 版,2009,32(5):632-635.
[3] Karam K Y,Badawy M T S.A direct method for evaluating performance of horizontal axis wind turbines[J].Renewable and Sustainbable Energy Reviews,2007(5):52-55.
[4] 周培毅.风力发电机组圆柱齿轮的故障振动分析[J].华东电力,2008(6):70-72.
[5] 张小宾.兆瓦级风力发电机增速器齿轮传动受力分析[J].机械工程师,2007(4):66-67.
[6] 高学敏.风力发电机组传动系统的研究[D].北京:华北电力大学,2007.
[7] 魏义存.风电齿轮啮合瞬态性能分析[D].北京:华北电力大学,2008.
[8] 朱仁胜,房 震,蒋东翔,等.基于 MW级风力机齿轮啮合的有限元分析[J].机械设计与制造,2012(6):31-33.
[9] 雷 镭,武宝林,谢新兵.基于ANSYS有限元软件的直齿轮接触应力分析[J].机械传动,2006,30(2):50-52.
[10] Larsson R.Transient non-Newtonian elastohydrodynamic lubrication analysis of an involute spur gear[J].Wear,1997,207(1/2):67-73.
[11] 机械设计手册编委会.机械设计手册:第3卷[M].北京:机械工业出版社,2004:1478-1490.

