线性回归模型在北京平原地面沉降预测中的应用

范珊珊，郭海朋，朱菊艳，李文鹏

(1.中国地质大学(北京)水资源与环境学院，北京 100083;2.中国地质环境监测院，北京 100081;3.中国地质调查局水文地质环境地质调查中心，河北保定 071051)

0 引言

北京作为国家首都，一座国际性的大都市，随着城市规模的不断扩大，经济的快速发展和人口的持续增长，对水资源的需求量不断增加，由于大量开采地下水，造成地下水位大幅下降，导致北京平原形成了大面积的地面沉降区。由于北京平原的范围太广，本文选择地面沉降较严重的天竺地区作为典型研究区域，进而推断整个北京平原地面沉降的发展趋势。

随着数值模拟技术的快速发展，以地面沉降理论为基础，利用计算机建立了大量的地面沉降预测模型，其中应用比较广泛的有灰色预测模型，包括GM(1，1)模型［1-2］和 GM(2，1)模型［3］，BP 神经网络模型［4-5］以及 MODFLOW 模型［6］等。近年来，建立地下水开采与地面沉降的线性回归方程也被广泛地应用于地面沉降的预测［7］。这种方法主要是依据最小二乘法原理得到回归方程的系数，建立地下水开采和地面沉降的线性回归方程，从而对沉降量进行预测。可以用于线性回归分析的软件主要有Excel和SPSS，由于Excel使用普遍，操作简单，本文的回归分析主要是应用这种方法。

1 地下水开采与地面沉降的相关性分析

由于长期超量开采地下水，造成地下水位的大幅度下降，导致含水层上覆土层的孔隙水压力减小，使土层失水压缩固结，从而形成地面沉降。所以，地面沉降与地下水开采存在着一定的相关性。图1为北京市天竺地区中深部地层沉降的变化与该层段内地下水水位变化曲线图，从图中可以看出，地面沉降量的变化趋势与地下水水位变化趋势基本一致。图2为累积地面沉降量和累积地下水开采量曲线图(考虑到地面沉降对地下水位下降有一定的滞后性，所以在分析时采用累积沉降量和累积开采量，从而减少滞后带来的影响［8］。)，如图1所示，地面沉降量随着地下水开采量的增加而增大。由此可见，地面沉降和地下水开采的相关程度较高。下面就对沉降量和地下水开采量或地下水水位的相关性进行定量分析。

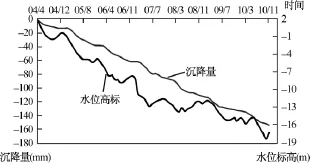
图1 地面沉降量和地下水位变化曲线图Fig.1 Curves of subsidence quantity and groundwater level variation

图2 累积沉降量和累积开采量曲线图Fig.2 Curves of accumulative subsidence quantity and accumulative groundwater mining

表1为2005～2009年北京天竺地区地面年沉降量［9］和地下水开采量［10］统计表。

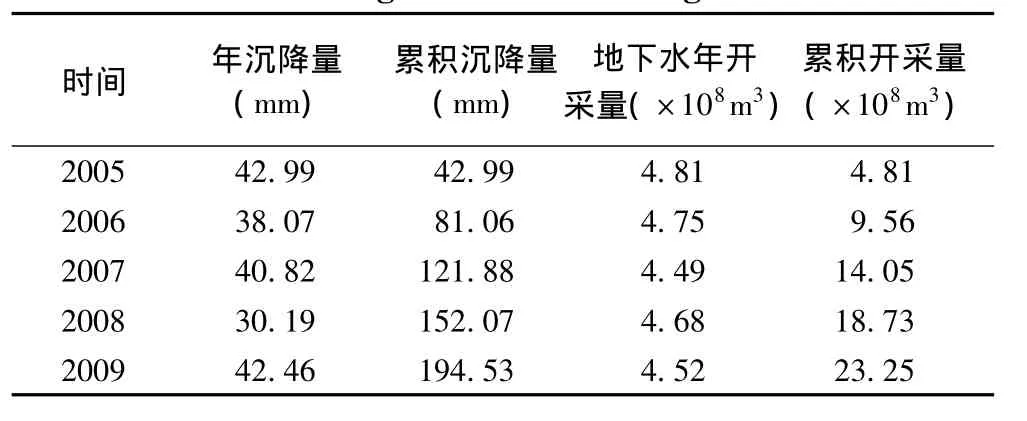
表1 天竺地面年沉降量和地下水开采量统计表Table1 Statistical table of Tianzhu subsidence quantity and groundwater mining

根据相关系数的判别规则，r＞0表明地面沉降量和地下水开采量成正相关，与地下水开采量和地面沉降量的曲线图(图2)所呈现的趋势是一致的，即随着地下水开采量的增加，沉降量也会增大。当相关系数在0.8≤r≤1时，两个变量之间为高度相关，所以地面沉降量和地下水开采量的相关性十分显著，可以建立线性回归方程。

同理利用Pearson相关系数的计算公式可以得到地面沉降量和地下水水位的相关系数为r=0.98596，根据以上分析过程，地面沉降量和地下水位之间也呈高度相关，同样适宜建立线性回归方程。

2 线性回归分析

2.1 地面沉降量与地下水开采量的线性回归分析

回归分析是指从一些反映某些变量之间关系的观测值出发，分析变量间的相关程度，并建立回归模型来拟合变量间的关系，从而提高对变量之间关系的认识。根据自变量的数量多少，回归分析可以分为一元回归分析和多元回归分析;根据自变量和因变量之间的关系类型，可以分为线性回归分析和非线性回归分析。本文所选择的是一元线性回归模型来进行研究，回归分析的主要任务就是根据若干个观测值找出两个变量x，y之间的线性关系，从而得到两者间的线性回归方程^y=ax+b，其中^y是y的估计值。求回归方程的过程，实际上是用回归直线对各个观测值进行拟合的过程，最常用的方法是最小二乘法。由于最小二乘法的计算过程非常繁琐，通常借助Excel软件的数据分析工具来进行回归分析。

将表1中的累积开采量和累积沉降量的一系列数据输入到Excel中，利用回归分析工具得到的分析结果如图3所示，通过分析结果中的数据可以得到线性回归方程的系数，即斜率 a=8.121，截距 b=4.156。

图3 Excel回归分析输出结果Fig.3 Output results of excel regression analysis

从而建立累积地面沉降量和累积地下水开采量的线性回归方程:s=8.121 Q+4.156

式中:s——累积地面沉降量;

Q——累积地下水开采量。

图4为累积地面沉降量和累积地下水开采量的线性回归直线，通过图表法得到的线性回归方程与利用回归分析工具得到的方程是一致的。从图4中还能够看出回归方程的判定系数R2=0.997，这表明自变量对因变量的解释程度较高，即总体的地面沉降有很大比例是由地下水开采引起的，判定系数可以用来衡量回归直线的整体拟合效果。

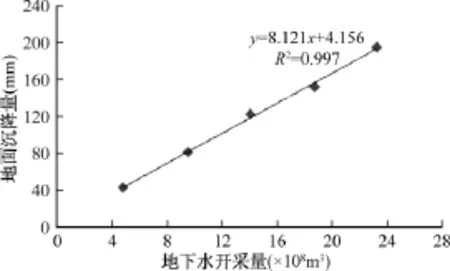
图4 累积沉降量和累积开采量的线性回归直线Fig.4 Linear regression line between accumulative subsidence quantity and accumulative groundwater mining

2.2 地面沉降量与地下水水位的线性回归分析

利用2004～2008年天竺地区中深部地层沉降量和地下水水位的观测数据同样可以得到地面沉降量和地下水位的线性回归方程(图5):

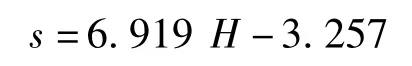
式中:s——中深部地层沉降量;

H——地下水水位。

图5 Excel回归分析输出结果Fig.5 Output results of excel regression analysis

图6为地面沉降量和地下水水位的线性回归直线，从图中可以得到该回归方程的判定系数R2=0.972，表明回归直线的拟合效果较好。

上述两个方程是从面和点两个不同层面上对地面沉降和地下水开采的相关性进行分析，它们的判定系数分别为0.997和0.972，说明回归直线的整体拟合效果都很好。所以，可以分别利用地下水开采量和地下水水位对地面沉降量进行预测。

3 线性回归方程的验证和预测

3.1 地面沉降量与地下水开采量回归方程的验证和预测

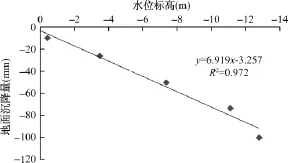
图6 地面沉降量和地下水位的线性回归直线Fig.6 Linear regression line between subsidence quantity and groundwater level

根据回归方程 s=8.121Q+4.156，将2005～2011年的地下水开采量代入其中，可以得到对应的地面沉降量预测值(表2、图7)。2010年和2011年是新输入的年份，所以不如前五年的拟合程度好，但总体趋势是吻合的。为了研究预测值的可靠程度，可以引入统计学中的置信区间来进行检验，即在一定置信度下所要预测的变量的可能取值范围。这里取置信度为95%，根据标准正态分布表可以得到置信度95%的置信区间为(s-1.96δ，s+1.96δ)，δ是由回归分析得到的标准误差，用来表示变量s偏离回归直线的误差。在线性回归直线s=8.121Q+4.156的上下作两条平行直线(图8):

表2 地面沉降量的真实值和预测值Table2 The measured and predicted values of subsidence quantity

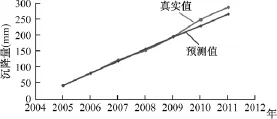
图7 地面沉降量的真实值和预测值拟合图Fig.7 Fitting curves of the measured and predicted values of subsidence quantity

s'=8.121Q+4.156-1.96δ和 s″=8.121Q+4.156+1.96δ

从图8中可以看出，2010和2011年累积沉降量真实值都落在置信度为95%的置信范围内，因此通过线性回归方程得到的沉降量预测值可靠程度较高。

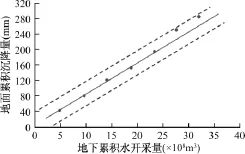
图8 回归方程的预测值可靠性检验图Fig.8 The reliability of predicted values based on regression equations test chart

假定2012～2014年地下水开采量将会维持2011年的现状开采水平，那么可以根据回归方程得到预测的累计沉降量，从而算出年沉降量的预测值(表3)。

表3 2012～2014地面年沉降量的预测值Table3 Predicted values of subsidence quantity between 2012 and 2014

从表3可以看出，在现状开采条件下，2012～2014年的年沉降量在2011年的基础上略有增加或基本持平，地面沉降持续发展，累积沉降量逐年增加。

3.2 地面沉降量与地下水位回归方程的验证和预测

将2004～2010年天竺地区中深层地下水水位观测值代入方程，可以得到中深部地层的沉降量预测值(表4)。沉降量的预测值和真实值的拟合程度较好(图9)。

表4 2004～2010年中深部地层沉降量的真实值和预测值Table4 Predicted values of subsidence quantity in middle-deep strata

将3.1中预测值可靠程度的验证过程同理应用到该方程预测值可靠性的分析过程中，可以得出根据地下水位预测的地面沉降量同样是十分可靠的。进行预测时可以将预计的地下水位标高值输入到方程中，从而预测同层段内的地面沉降量。

4 结论

(1)通过对北京天竺地区地下水开采和地面沉降的关系进行分析，可以看出两者之间具有一定的线性关系，通过地下水开采量或地下水水位，可以对地面沉降量进行预测。

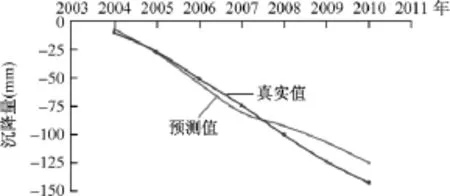
图9 地面沉降量的真实值和预测值拟合图Fig.9 Fitting chart of the measured and predicted values of subsidence quantity

(2)建立线性回归方程操作简单，工作量小，但是预测误差是不可避免的。由于资料有限，本文建立的预测模型没有考虑地面沉降的其它影响因素如地层岩性、地面荷载等。在以后建立的线性回归模型中，如果可以将多种影响因素一起考虑，那么预测精度将会有很大提高。

(3)由以上分析，北京天竺地区地面沉降的变化趋势与地下水水位变化趋势基本一致，地面沉降量与地下水开采量具有高度的相关性，可以推断出北京平原地面沉降产生的主要原因是地下水的大量开采。

(4)通过模型预测可知，在维持地下水现状开采的条件下，不考虑其它影响因素，北京平原区的地面沉降将会持续发展，整体的地面沉降量仍会继续增加。

［1］赵显富，郭淳.灰色预测模型及其在沉降预测中的应用［J］.铁路航测，2002，28(3):30-32.ZHAO Xianfu，GUO Chun.Gary forecast model and it's application in settlement observation［J］.Railway Air Survey，2002，28(3):30-32.

［2］兰孝奇，严红萍，刘精攀.灰色系统预测模型在沉降监测中的应用［J］.现代测绘，2006，(1):24-26.LAN Xiaoqi，YAN Hongping，LIU Jingpan.The gary model application for settlement observation［J］.Modern Surveying and Mapping，2006，(1):24-26.

［3］郑良飞，折学森.地面沉降的GM(2，1)模型预测研究［J］.中国地质灾害与防治学报，2007，18(4):66-69.ZHENG Liangfei，ZHE Xuesen.A study to the ground settlement forecast with GM(2，1)model［J］.The Chinese Journal of Geological Hazard and Control，2007，18(4):66-69.

［4］周复旦，赵长胜，高卫东.BP神经网络模型在采水地面沉降中的应用研究［J］.测绘科学，2011，36(6):233-234.ZHOU Fudan， ZHAO Changsheng， GAO Weidong.Application ofBP neuralnetwork modelto ground subsidence of mining water area［J］.Science of Surveying and Mapping，2011，36(6):233-234.

［5］金爱善.采用神经网络模型对天津滨海新区地面沉降预测的研究［J］.现代地质，2000，14(4):475-478.JIN Aishan.Prediction of land subsidence in the new coastal region of Tianjin with artificial neural network model［J］.Geoscience，2000，14(4):475-478.

［6］宋小军.基于MODFLOW对天津宁河县的地面沉降预测研究［J］.矿产勘查，2010，1(6):564-568.SONG Xiaojun. Research on prediction of land subsidence based on MODFLOW in Tianjin Ninghe county［J］.Mineral Exploration，2010，1(6):564-568.

［7］马锋，杨发俊，陈润桥，等.天津市地下水开采对地面沉降影响的多元回归分析［J］.中国地质灾害与防治学报，2008，19(2):63-66.MA Feng，YANG Fajun，CHEN Runqiao，et al.Effect of groundwater exploitation on land subsidence in Tianjin using multiple regression analysis method［J］.The Chinese Journal of Geological Hazard and Control，2008，19(2):63-66.

［8］谭荣初.吴江市地面沉降与开采地下水关系的研究［J］.水资源保护，2002(2):48-50.TAN Rongchu.Relationship between ground settlement and groundwater exploitation in Wujiang City［J］.Water Resources Protection，2002(2):48-50.

［9］杨艳，贾三满，王海刚.北京平原区地面沉降现状及发展趋势分析［J］.上海地质，2010，31(4):23-28.YANG Yan，JIA Sanman，WANG Haigang.The status and development of land subsidence in Beijing Plain［J］.Shanghai Geology，2010，31(4):23-28.

［10］北京市水务局.北京市水资源公报［R］.2005-2009.Beijing Water Authority. Beijing Water Resources Bulletin［R］.2005-2009.