区域科技投入与经济增长关系的实证研究——以河北省为例
张少津,刘文艳
(1.河北省标准化研究院 条码中心,河北 石家庄 050091;2.石家庄经济学院 商学院,河北 石家庄 050031)
新经济增长理论把技术因素作为经济系统的内生变量,认为经济增长根源于知识和人力资本的增长,技术进步是经济增长的决定因素。①河北省作为以传统经济为主的经济大省,在政府主导的“科教兴冀”战略的影响下,科技对经济经济增长的作用正在逐步增强。但是,科技因素是否能够像新经济理论所倡导的那样,正在成为经济增长的决定因素,这不仅是经济学界的一个理论问题,更重要的是,这关系到未来河北省经济是否能够持续、稳定增长,也将关系到经济增长质量问题,即经济增长模式是否能够由“粗放式”转变为“集约式”。要回答上述问题,必须要进行客观的、定量的研究,探讨河北省科技与经济增长的关系。基于此,本文将专门选取科技活动投入经费、科技人员投入作为科技投入指标,选取地区国内生产总值作为经济增长指标,应用协整理论和向量自回归理论进行定量研究。
一、数据选取和变量说明
在变量的选取过程中,为保证数据的准确性和权威性,本文选择的科技投入仅指科技活动经费和从事科技活动人员,用地区生产总值作为测度区域经济增长的指标。所取数据来源于《河北省经济年鉴》《中国科技年鉴》。考虑到数据的可获得性、连续性等因素,研究选取1993—2010年河北省国民生产总值(GDP)作为衡量经济增长的被解释变量;选取同期的河北省科技活动经费(KY)、从事科技活动人员(RY)作为解释变量来衡量科技投入的指标。同时,为保证数据的可比性,消除通货膨胀因素,研究首先利用物价指数对名义地区生产总值和名义科技活动经费进行折算(以1978年不变价折算)。为使数据尽量平稳,也为了消除变量间的异方问题,对三类数据分别取自然对数,表示为LnKY、LnRY和LNGDP,上述变换不会改变变量间的长期均衡关系和短期动态稳定关系。
二、计量经济学分析
(一)单位根检验
首先,对三组变量进行平稳性检验,在对地区生产总值、从事科技活动人员、科技活动经费内部支出所对应的对数序列的单位根检验过程中,本文先利用ADF检验法对各个序列的平稳性进行检验。检验结果(见表1)显示,三组变量均为非平稳序列,不能用来直接构建计量经济学模型。因此,对三组变量分别进行差分处理,取各自的一阶差分,再进行ADF检验,在5%显著性水平下通过平稳性检验。因此,LnGDP、LnKY和LnRY为一阶单整,即三个变量均为I(1)序列。由于序列之间存在同阶单整,因此这三个变量满足进行协整检验的前提条件,可以对其进行协整分析。

表1 LnGDP、LnRY和LnKY的单位根检验
(二)构建向量自回归模型(VAR模型)
由于向量自回归模型是以内生变量作被解释变量,以变量本身的滞后变量作为解释变量构建的计量经济学模型。因此,构建向量自回归模型的关键点是确定合理的滞后期。为此,在表2中试算了模型的0至3期滞后,结果显示,以LR、FPE、AIC、SC和HQ五个判断标准进行分析,可以得出该模型的最优滞后期为2,即该模型为VAR(2)。

表2 VAR模型滞后期的选择

图1 VAR(2)平稳性检验结果
如图1所示,在VAR(2)模型中,单位圆内包含了所有根模的倒数,可以判断出以此建立的模型稳定。同时,也可以判断出在此基础上所进行的脉冲响应函数和方差分解分析有效②,进而可以得到VAR(2)模型如方程(1)、方程(2)和方程(3)所示。

(三)协整检验
由计量经济学理论知道,同阶单整是进行协整分析的前提。前面部分的单整检验结果显示,取自然对数后的三组数据构成一阶单整序列,因此可以进行下一阶段的协整分析。本文应用协整理论中的E-G两阶段检验法对三变量进行协整检验,该方法分为两个阶段,第一个阶段是构建一般最小二乘估计模型,通过检验后,以残差为被解释变量再次构建一般最小二乘估计模型;第二个阶段是对残差的平稳性进行单位根检验,残差平稳检验后,可以说明研究变量间存在协整关系,即存在长期均衡关系。具体如下:
第一步,对三变量使用普通最小二乘法(OLS)回归,得到协整方程(4):
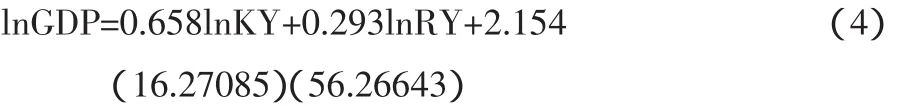
该回归模型的拟合优度(R2)为0.965 7,可以通过模型的总体检验,两个解释变量的T值分别为16.27085和56.26643,远大于临界值,说明模型能够通过变量的检验。综合总体检验和变量检验,协整方程能够通过显著性检验。
进一步建立残差回归模型如下:

第二步,残差平稳性检验。检验方法仍旧采用ADF检验,计算的ADF值为-3.68239,可以查出5%临界值为-1.96843。比较显示,ADF值低于显著性水平5%临界值,可以拒绝残差序列不平稳的原假设,接受残差序列为平稳序列的判断(见表3)。
上述模型分析,可以得出如下结论:科技活动经费投入、科技活动人员投入和经济增长之间存在长期协整关系。模型数据进一步显示,科技活动经费增加1%,河北省经济增长0.658%;科技人员增加1%,经济增长0.293%。

表3 残差平稳性检验结果
(四)格兰杰因果关系检验
协整检验可得出时间序列之间是否存在长期的均衡关系,但还不能说明解释变量与被解释变量之间存在必然的因果关系,而序列之间的因果关系可用格兰杰(Granger)因果关系检验法进行检验。其基本思想是:如果变量Xt是Yt的原因,则Xt的变化应先于Yt的变化。因此,在作对其他变量的回归时,如果把Xt的滞后值包括进来能显著地改进对Yt的预测,则称Xt是Yt的Granger原因,否则称Xt不是Yt的Granger原因。
为了能够说明科技投入(科技活动经费投入、科技活动人员投入)和经济增长之间的因果关系,分别作出LnGDP和LnRY、LnGDP和LnKY之间的相互回归模型,即要作出四个模型,考虑滞后因素,研究分别选取滞后期1和滞后期2进行建模,这样需要进行8个模型的构建和检验,具体结果如表4。
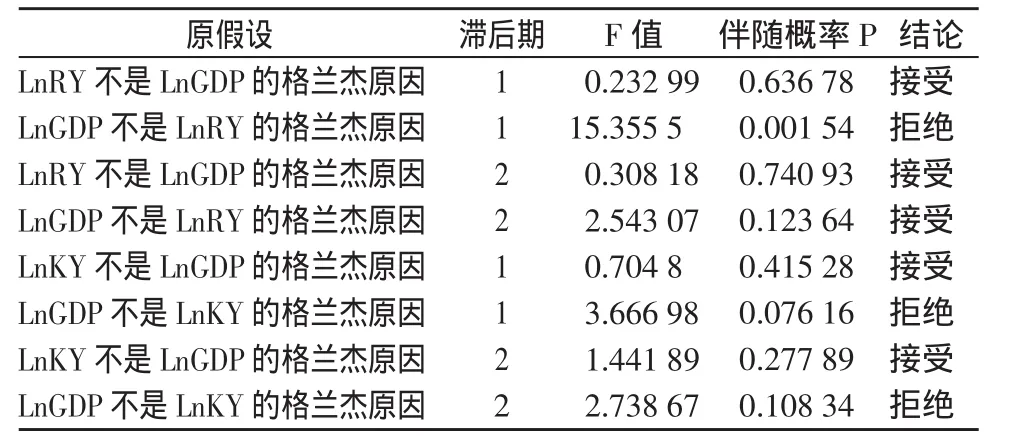
表4 各变量Granger因果关系检验
根据以上的格兰杰因果关系检验结果表明,滞后一期时,LnGDP不是LnRY的格兰杰原因的概率为0.001 54,拒绝原假设,说明经济增长带动就业增加了从事科技活动人员的数量。LnRY不是LnGDP的格兰杰原因的概率为0.504 28,接受原假设,说明单纯增加从事科技活动人员的数量并不能直接带来经济的增长。滞后两期时两者互不为格兰杰因果关系。另外,滞后一期时,LnGDP不是LnKY的格兰杰原因的概率为0.076 16,拒绝原假设。滞后两期时,LnGDP不是LnKY的格兰杰原因的概率为0.108 34,接受原假设,说明经济增长促使科技活动经费增加,但是科技活动经费增加并没有带来经济的增长。以上结论表明,河北省经济增长仍然是粗放式增长,科技投入并不能给经济注入强劲的生长力。
(五)脉冲响应函数分析
之所以要进行脉冲响应函数分析,原因是协整模型仅能揭示出变量间是否存在稳定的均衡关系,格兰杰检验尽管能够显示出解释变量和被解释变量的因果关系,但是上述两类方法均不能提供动态信息,即不能提供当一个变量作用于另一个变量的动态变化特征。为此,借助于前期研究所建立的向量自回归模型[LnGDP作被解释变量、LnKY作解释变量的VAR(2)模型和LnGDP作被解释变量、LnRY作解释变量的VAR(2)模型]进行脉冲响应分析。本文采用了广义脉冲法,分析结果如图2、图3所示。
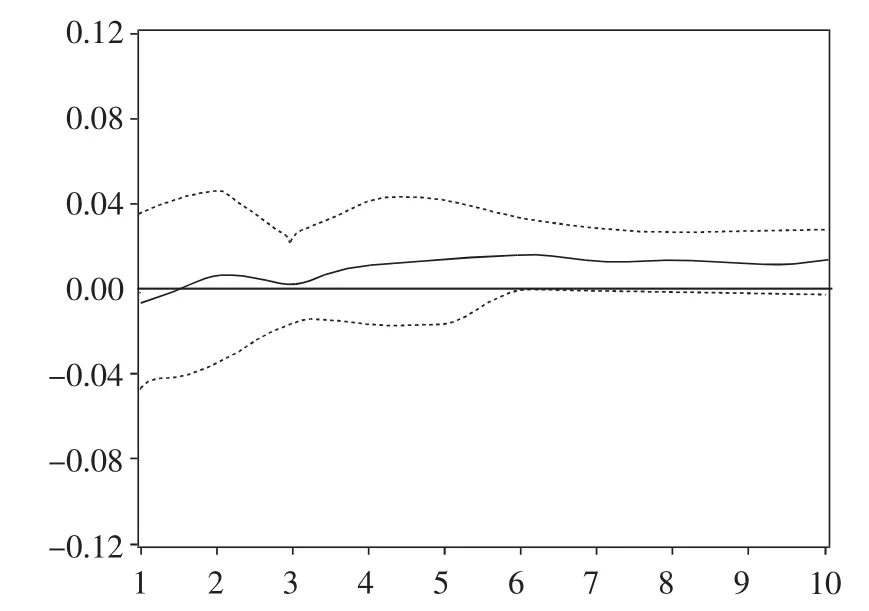
图2 LnRY对lnGDP的脉冲响应
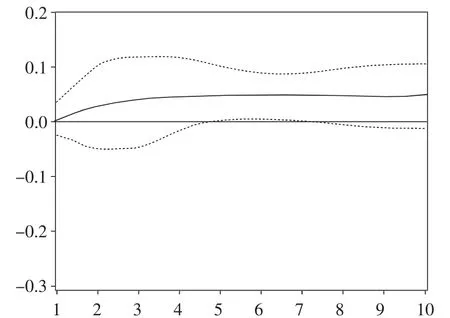
图3 LnKY对lnGDP的脉冲响应
图2和图3显示,从事科技活动人员投入变动和科技活动经费投入变动对经济增长的冲击始终大于0,并且曲线斜率也大于0,但斜率呈现递减趋势。这说明,作为科技投入指标的科技活动经费投入和科技活动人员投入变化对河北经济增长变化有正向影响,但是作用效果趋于缓和,即说明科技投入对经济增长作用效果方面存在着类似于消费者行为理论中的“边际效用递减”现象。
(六)方差分解
为了更加精确地分析代表科技投入的科技活动经费投入和科技活动人员投入对河北省经济增长变化的影响,在研究方法方面,借助于方差分解研究法。该方法的主要思想是通过分析每一个结构冲击对内生变量变化的贡献度来评价不同结构冲击的重要性③。本部分研究使用的向量自回归模型是前面部分中的方程(1),对LNGDP的标准误差(S.E.)进行了分解(具体结果见表5)。
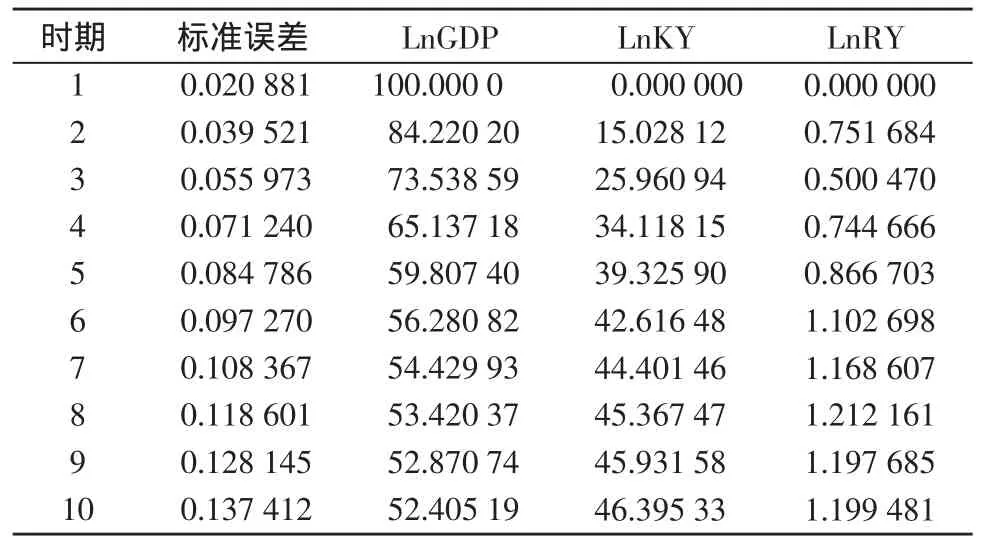
表5 LNGDP方差分解
表5显示了从第1期到第10期的标准差分解,即:河北省经济增长的标准误差被分解成经济增长(LnGDP)和科技活动经费(LnKY)、从事科技活动人员(LnRY)三部分,各部分在不同时期的贡献互不相同。
从总体趋势分析,无论是科技活动经费投入(LnKY),还是科技活动人员投入(LnRY),随着滞后期的增加,对经济增长(LnGDP)变化的贡献呈现出递增趋势;从相对比重角度分析,科技活动经费投入(LnKY)对经济增长变化的贡献比重远高于科技活动人员投入(LnRY)的比重。这说明,科技活动经费投入相对于科技人员投入对经济增长变化的贡献度大,并且随着滞后期的增加,这一贡献度不断增大。
三、结论与初步建议
经过系列定量分析,得到如下结论:第一,从协整分析结果可以看出,河北省科技投入和经济增长符合协整关系,即两者间存在长期的均衡关系;第二,从格兰杰因果关系分析可以看出,河北省经济增长是科技投入的单向格兰杰原因,反之的因果关系并不明显,这说明河北省经济增长中科技的因素贡献程度不高,经济增长模式仍然是粗放型;第三,从脉冲响应函数结果可以看出,科技投入变化对河北省经济增长变化有正向影响,但是作用效果有变缓趋势,说明增加科技投入有助于经济增长,但随着时间推移,科技投入对经济增长的作用效果在减弱;第四,从方差分解结果可以看出,科技活动经费投入与科技人员投入相比较,科技活动经费投入的变化对经济增长变化的贡献程度大。
针对上述研究,提出如下建议:其一,从因果关系结果角度分析,由于河北省科技投入和经济增长之间具有长期均衡关系,同时,经济增长是科技投入增加的格兰杰原因,因此,促进经济增长有利于科技规模的扩大,增强科技实力。其二,从科技投入增量变化对经济增长的效果看,增加科技投入有利于经济增长,因此,必须坚持加大科技投入的政策思路。其三,从科技活动经费投入和科技人员投入作用看,科技活动经费投入对经济增长的作用更强,说明科技人员数量的增加并不是关键问题,更为关键的是科技人员的业务素质和科研业绩。因此,加大科技活动经费投入并内化到科技人员自身,以提高科技人员的业务素质和科研业绩,进而对经济增长发挥作用,这也从一个侧面再次证实了“科教兴冀”战略的正确性和长久性。
[1]李京文,郑友敬.技术进步与经济效益[M].北京:中国财政经济出版社,1989:23-25.
[2]熊德斌.贵州省消费结构与产业结构的实证检验[J].统计与决策,2009,(11):117-119.
[3]高铁梅.计量经济分析方法与建模EViews应用及实例[M].北京:清华大学出版社,2006.

