砰击载荷作用下船艏结构瞬态响应研究

任慧龙，翟帅帅，于鹏垚，李辉，刘洋

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001

砰击载荷作用下船艏结构瞬态响应研究

任慧龙，翟帅帅，于鹏垚，李辉，刘洋

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001

砰击现象对高速舰船艏部局部结构破坏相当严重，对舰船和人员的安全构成较大威胁，然而由于砰击载荷的瞬态性和强非线性，其计算理论还很不成熟，舰船艏部结构在砰击作用下的应力响应更鲜有人研究。基于此，利用设计波下确定的砰击压力极值，结合以往试验测定的砰击压力随时间的变化关系，计算得到砰击压力的时空分布，然后将其施加在船艏精细有限元模型上，利用中心差分法进行数值计算，并对计算中一些关键参数的设置值做不同尝试，得到了较理想的艏部结构应力响应历程。

砰击；非线性；船艏；数值模拟；瞬态响应

0 引 言

近几十年来，由砰击造成的海损事故不胜枚举，调查数据表明，历史上10%～12%的海损事故由剧烈的砰击引起，对高速航行的舰船来说，就更加需要对砰击问题给予重视。国内外不少学者都对船舶砰击问题进行过研究，例如，唐友刚、陆鑫森、王刚、卢炽华等［1－4］对砰击压力及由砰击引起的振动问题进行了研究，任淑霞、陈震、朱加刚、Bereznitski和Samuelides等［5－9］在数值仿真方面进行了探讨。

目前，业界存在着几种不同的预测砰击载荷的理论，然而，由于砰击现象的瞬态性和强非线性，不同的理论在预报砰击载荷极值和作用时间上存在较大差别。因此，在理论计算的基础上，结合船模试验测量值，本文将对砰击载荷极值和砰击作用时间进行适当修正。

另外，在进行舰船砰击作用下的动态响应计算时，因存在工作量巨大、计算机内存需求较高等问题，目前尚未见有人对船艏精细结构做过有限元数值分析，大多数情况下要么是将动态过程处理成准静态问题，要么是分析局部结构在局部载荷作用下的动态响应，但这些方法在预报舰船整体结构响应上存在精度不高的问题。基于此，为了解船艏在一个完整砰击载荷周期内的整体响应情况，同时为了保证有限元数值计算结果能更准确地反映舰船在实际运营状态下的应力响应，本文将对船艏进行精细建模，将时空分布的艏部砰击压力载荷施加在有限元模型上，采用直接法对模型进行瞬态分析，并对数值计算过程中的关键参数做不同的尝试，以得到较理想的船艏局部结构应力响应时程。通过对应力结果的分析，所得结论可为高速舰船设计者们提供很好的借鉴意义。

1 载荷计算及求解方式

1.1 船艏结构入水历程

夏斌等［10］在研究弹性结构物的入水过程时，将其分为了3个阶段：第1阶段为结构物底部接触水面之前的阶段，在此阶段中，结构物底部的载荷为零；第2阶段为结构物底部与水面开始接触的阶段，在此阶段，冲击压力迅速上升并达到峰值；第3阶段为结构物在水中下沉的阶段，在此阶段，结构物主要受重力和浮力的影响。受此启发，并结合试验中船艏结构的实际入水情况，本文将艏部结构入水也分为了3个阶段：第1阶段为艏部结构还未与水面接触的阶段，此时砰击载荷为零；第2阶段为结构发生底部砰击至舷侧发生外飘砰击这一阶段，此时的船艏主要受砰击载荷作用，同时艏部结构在浮力的作用下入水速度有较明显的下降；第3阶段为船艏结构继续下沉至艏部结构出水为止的阶段，在此过程中，艏部结构主要受重力和浮力的作用。船艏结构入水历程示意图如图1所示。

图1 艏部结构入水历程Fig.1 Slamming progress of bow structure

1.2 底部砰击

1.2.1 砰击时间

图2 底部砰击压力试验测量值Fig.2 Pressure of bottom slamming by ship model

1.2.2 砰击压力

至今，已有很多学者对压力、船型及速度这三者之间的关系进行过理论和试验探讨，其给出的最大压力表达式为

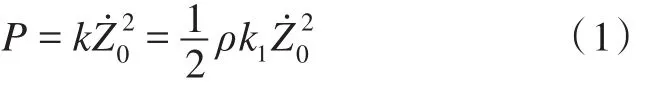
式中：k为剖面形状系数；k1为无因次的k值，两者的取值可通过船模试验测量得到，或者通过Ochi提供的回归方程或估算曲线进行确定［11］；为砰击瞬时垂向相对速度；ρ为水的密度。砰击压力的概率密度可通过理论推导得出：

1.3 外张砰击

1.3.1 砰击时间

对于外张砰击压力随时间的变化，目前鲜有人对此进行描述。根据曾经测量过的舰船模型外张压力信号，本文保守地确定外张砰击压力时间为0.1 s。某一工况下的外张砰击压力信号测量值如图3所示。

图3 外张砰击压力试验测量值Fig.3 Pressure of bow flare slamming by ship model

1.3.2 砰击压力

一般认为，外张砰击压力包括两个部分：由相对速度在水面的法向分量和切向分量引起的入水冲击压力pi和撞击冲击压力ps。如果假定流动是理想的，那么总的外张砰击压力p便是两者的压力之和，即

其中，入水冲击压力可写为

式中：Vn为入水冲击速度；Kw为无因次压力系数。Kw与冲击表面的有效冲击角相关，其取值可利用估算公式进行计算［11］。

撞击冲击压力为

其中，Ks可简单地取为4。

1.4 水动压力计算

在势流理论［11］的框架下，通常将波动压力划分为3种：入射波压力、绕射波压力和辐射波压力。在3种压力成分中，入射波压力的比重最大，考虑到砰击压力和浮力等的作用，绕射波压力和辐射波压力的影响很小。而且对应于合成压力作用下的响应最大值，砰击压力的贡献最大，而波动压力则主要影响应力响应下降段的形状，因此对于波动压力，本文将只考虑入射波的影响。浮力和入射波压力的求解方程如下：

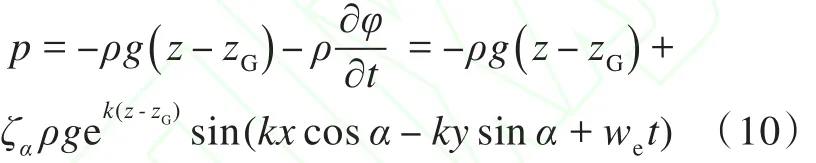
式中：α为波幅；we为波浪圆频率；k为波数；φ为入射波速度势。

根据舰船的航行海域，本文选取标准海浪资料No.34作为计算用的海浪统计资料，采用线性设计波法对本文所用舰船进行长、短期分析，确定巡航工况下的设计波参数值，然后根据上述理论计算得到船艏压力的时空分布，并根据船模试验测量值对计算结果进行适当修正。考虑到砰击的强瞬时性，以及结构的最大应力响应主要受压力最大值的影响，因此在砰击的前、中期将砰击载荷处理成了三角脉冲的形式。假设砰击极值压力为P，砰击作用时间为t，则砰击压力从零增大至极值压力的函数表达式为Pt=2×P/t，在此阶段中，水动压力所占的比例很小，因而将忽略水动压力的影响。在砰击后期和船艏出水阶段，砰击压力明显减小，水动压力迅速增大，此时，将综合考虑两者的作用。下面将给出不同纵向位置（x=192，203，210 m）和不同垂向高度（z=7，10，13，16，18.5 m）处压力的时空曲线，如图4～图6所示。

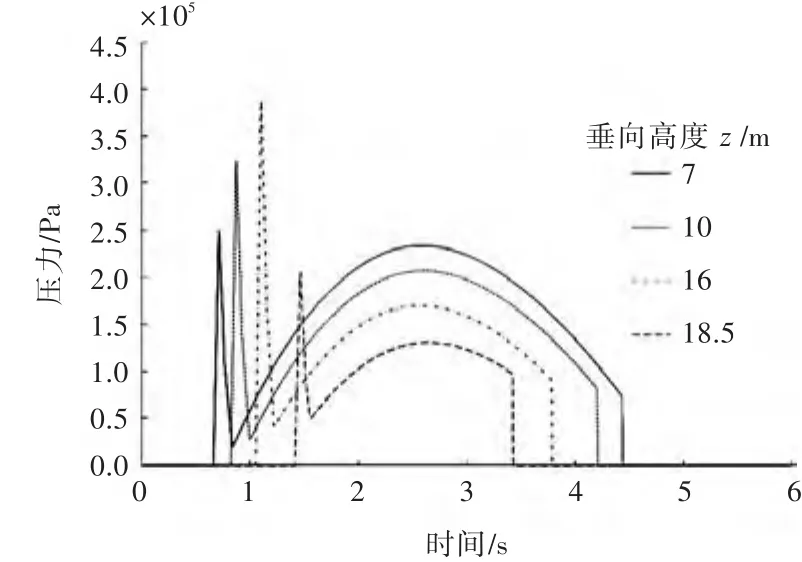
图4 x=192 m处剖面压力信号Fig.4 Pressure of different vertical positions at the longitudinal positionx=192 m

图5 x=203 m处剖面压力信号Fig.5 Pressure of different vertical positions at the longitudinal positionx=203 m

图6 x=210 m处剖面压力信号Fig.6 Pressure of different vertical positions at the longitudinal positionx=210 m

注意，砰击过程是一个连续变化的过程，并不存在明显的突变时刻而可将砰击过程分成几个典型的阶段，且目前所见的文献中也未见有学者在此方面做过探讨，至于本文所提到的砰击前、中、后期，是为了便于描述而进行的定性划分。认为砰击的前、中期是砰击压力从零增大到极值压力并有些许下降的一段，在此阶段可以忽略水动压力的影响，而砰击后期则是指在此阶段砰击压力值已有明显的下降，在此阶段水动压力的影响不可忽略。

2 船艏结构瞬态响应分析

2.1 直接瞬态响应计算

以某舰船为研究对象，利用有限元前处理软件MSC.PATRAN对艏部结构进行精确建模。为保证有限元模型包含发生砰击的所有区域，本文对此舰船的前1/3结构进行了精确建模，考虑到砰击是短时间内的强非线性动力响应，可以将船艏看成是自由结构［12］。由于砰击载荷的强瞬时性，其主要影响船艏局部的应力响应，另外考虑到计算的可行性，因此本文将只考虑船艏结构在砰击载荷作用下的响应规律。所建立的模型中共有22 594个节点，45 265个单元。利用已编制好的PCL语言，将上述计算的砰击载荷施加于有限元模型，因外板上每一单元的砰击压力都不相同，因此需要在前处理软件MSC.PATRAN中对每个单元都建立载荷值随时间变化的场函数。砰击前、中期的压力值函数表达式已经在第1.4节中给出，而在砰击后期以及船艏出水阶段，将计算很多时刻的压力值，然后以表格的形式作为场函数的输入形式，而后再以压力的形式施加在相应的有限单元上。采用直接瞬态响应法进行求解，求解时间为船艏开始入水至船艏完全出水这一周期过程。运动方程的矩阵形式为

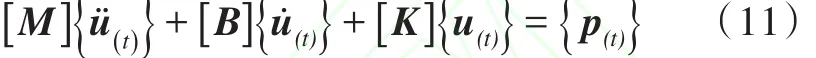
通过用中心差分法［13］来计算离散点处的速度和加速度

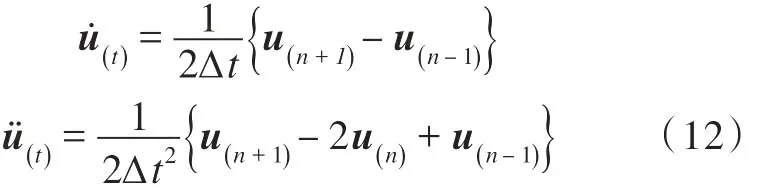
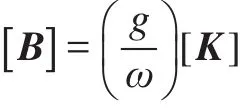
2.2 船艏应力响应结果

图7 x=192 m处对应单元应力响应Fig.7 Stress response of the elements at the longitudinal positionx=192 m

图8 x=203 m处对应单元应力响应Fig.8 Stress response of the elements at the longitudinal positionx=203 m

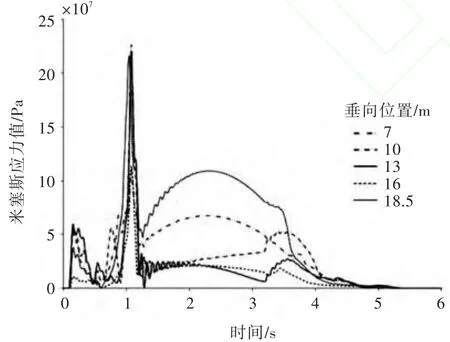
图9 x=210 m处对应单元应力响应Fig.9 Stress response of the elements at the longitudinal positionx=210 m

对应于前述载荷加载的单元，得到其应力响应时程曲线如图7～图9所示。从砰击载荷曲线和对应的有限单元应力响应曲线对比中，发现船艏结构的应力响应曲线与载荷输入曲线同步，而且应力最大值也出现在砰击载荷最大的时刻，整个结构在1 s左右应力响应达到最大。外，又因舰船的底部结构均有不同程度的加强，因此此时船艏底部结构的应力值不是很大，一般都在结构的静力屈服极限内。随着船艏的继续下埋，砰击发生部位迅速扩大，结构的应力响应值也随之迅速增大，此时船艏的砰击速度虽然不如刚发生底部砰击时大，但也在较大的速度值上，而且由于船艏外飘，此时发生砰击的单元较只发生底部砰击时要多很多。另从应力云图中也可以看出，此时船艏舷侧外板与其上肋板的应力值均较大，并且船艏结构在1 s左右就达到了最大应力响应值约400 MPa，对于本舰船来说，此时的应力值已经超过了所用钢材的静力屈服限，此时的船体结构很容易进入塑性变形阶段。之后，由于船艏在浮力的作用下砰击速度明显下降，砰击压力也随之很快下降。舰船在出水阶段不再受砰击作用，应力水平有了较明显的降低。

图10～图15所示为几个典型时刻的应力响应云图以及对应时刻船波相对位置示意图。从中可以发现，在砰击前期，由于船艏只有底部发生了砰击，砰击区域小且集中，因此其结构的应力响应基本与发生砰击的部位保持一致，虽然此时有些单元的砰击压力也不小，但其作用的范围很小，另

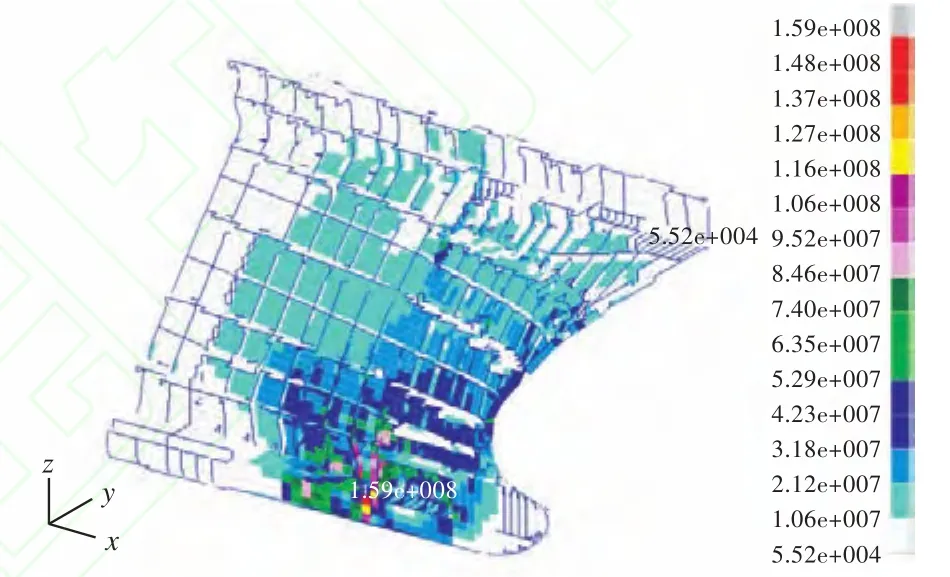
图10 t=0.3 s时的应力云图Fig.10 Stress contours at timet=0.3 s

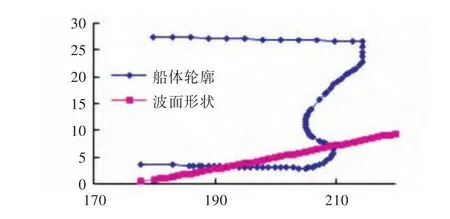
图11 t=0.3 s时的船波相对位置图Fig.11 Ship and wave's position at timet=0.3 s

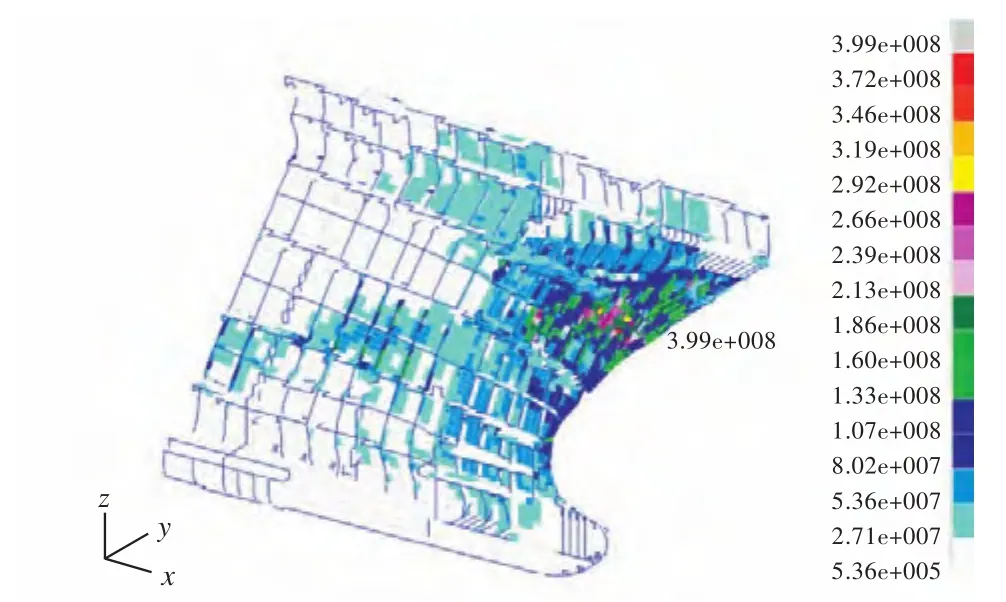
图12 t=1.0 s时的应力云图Fig.12 Stress contours at timet=1.0 s

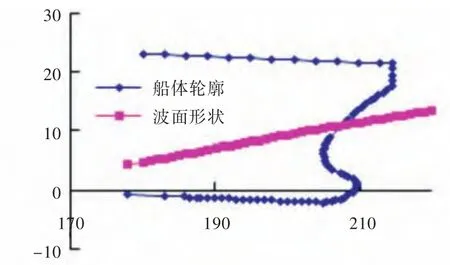
图13 t=1.0 s时的船波相对位置图Fig.13 Ship and wave's position at timet=1.0 s

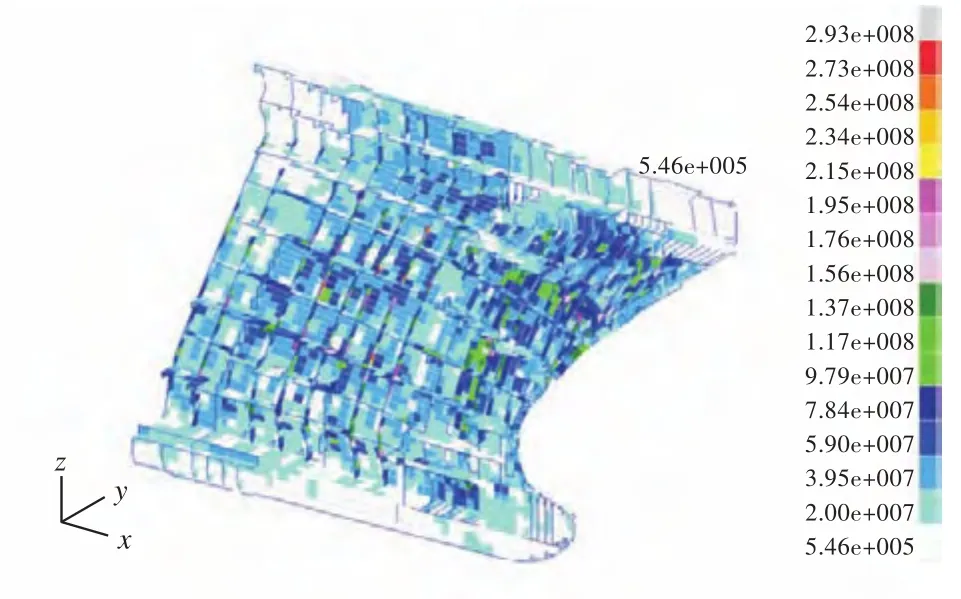
图14 t=2.4 s时的应力云图Fig.14 Stress contours at timet=2.4 s

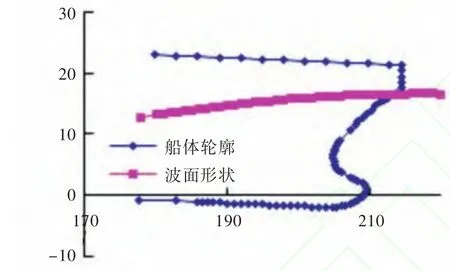
图15 t=2.4 s时的船波相对位置图Fig.15 Ship and wave's position at timet=2.4 s

3 结 语

本文通过对某舰船艏部结构在砰击载荷作用下的应力响应研究，给出了用直接瞬态响应计算时一些关键参数的设置参考值。经过对应力结果进行分析，发现船艏结构在承受砰击载荷作用时船体外板和肋骨的应力值较大，且大大超过了静力屈服极限，虽然文献［14］指出，对于大多数金属材料，动力屈服极限要比静力屈服极限高出1.5～3.5倍，但对设计者而言，也要考虑舰船在受到砰击载荷作用时船艏结构可能会发生的塑性变形和由此引起的舰船疲劳问题。

［1］ 唐友刚，董艳秋.Hamilton法计算肥大船砰击响应［J］.天津大学学报，1994，27（3）：370－374.

TANG Yougang，DONG Yanqiu.Application of Hamilton method in the calculation of slamming response of a full－form ship［J］.Journal of Tianjin University（Science and Technology），1994，27（3）：370－374.

［2］ 陆鑫森，叶伟，余国新，等.现代高速船结构设计问题［J］.上海交通大学学报，1996，30（10）：129－135，146.

LU Xinsen，YE Wei，YU Guoxin，et al.Structure design problems of modern high speed vessels［J］.Journal of Shanghai Jiaotong University，1996，30（10）：129－135，146.

［3］ 王刚.高速船舶结构设计中流体冲击载荷的数值计算［J］.船舶，1998（5）：26－30.

［4］ 卢炽华，何友声，王刚.船体砰击问题的非线性边界元分析［J］.水动力学进展与研究：A辑，1999，14（2）：169－175.

LU Chihua，HE Yousheng，WANG Gang.Hull slamming analysis by using nonlinear boundary element method［J］.Chinese Journal of Hydrodynamics（Ser.A），1999，14（2）：169－175.

［5］ 任淑霞.船舶结构砰击响应控制方法研究［D］.武汉：武汉理工大学，2003.

［6］ 陈震，肖熙.平底结构砰击压力的分布［J］.中国造船，2005，46（4）：97－103.

CHEN Zhen，XIAO Xi.The distribution of slamming pressure on flat－bottom structure［J］.Shipbuilding of China，2005，46（4）：97－103.

［7］ 朱加刚.船底结构砰击时的水弹性分析［D］.哈尔滨：哈尔滨工程大学，2006.

［8］ BEREZNITSKI A.3D model for bottom slamming［C］// Proceeding of the 20th International Conference on Offshore Mechanics and Arctic Engineering，2001：315－322.

［9］ SAMUELIDES M，SERVIS D P.Bow door slamming of Ro/Roferries［J］.Marine Structures，2002，15（3）：285－307.

［10］ 夏斌，陈震，肖熙.弹性平底海洋结构物入水冲击的仿真分析［J］.中国海洋平台，2005，20（1）：22－28.

XIA Bin，CHEN Zhen，XIAO Xi.The simulation analysis of the slamming of elastic flat－bottom marine structure［J］.China Offshore Platform，2005，20（1）：22－28.

［11］ 戴仰山，沈进威，宋竞正.船舶波浪载荷［M］.北京：国防工业出版社，2007：23－37.

［12］ 王娜.自由结构在强动载荷作用下的动力响应分析［D］.武汉：华中科技大学，2007.

［13］ BATHE K J，WILSON K J，WILSON E L，等.有限元分析中的数值方法［M］.北京：科学出版社，1985：348－357.

［14］ 徐秉业，刘信声.塑性力学及其在工程中的应用之讲座（七）：考虑应变率敏感性的塑形动力学［J］.机械强度，1984（3）：73－81.

Transient Response of the Bow Structure Under Slamming Loads

REN Huilong，ZHAI Shuaishuai，YU Pengyao，LI Hui，LIU Yang
College of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，China

The slamming phenomenon is ruinous to the bow structure of ships and is a grave threat to the safety of crew members，especially when ships are at middle and high speeds.Due to its inherent transient and strong non－linear property，the accurate simulation of the slamming process has been quite unsuccessful，and the response of the bow structure to the slamming has been rarely investigated.Therefore，this paper aims at calculating the slamming loads that varies with space and time by incorporating the maximum slamming load value under the design wave and the exact value of the slamming loads collected in former experiments.The transient response is then calculated by using the central difference method after the slamming loads impact the bow structure.Particularly，the time interval and a few key parameters for solving the problem are presented.The results show that the stress on different elements can be obtained accurately，which could be further used as references during the bow structure design.

slamming；non－linear；bow；numerical simulation；transient response

U661.43

A

1673－3185（2013）06－14－06

10.3969/j.issn.1673－3185.2013.06.003期刊网址：wwwwww.sshhiipp－rreesseeaarrcchh.ccoomm

http://www.cnki.net/kcms/detail/42.1755.TJ.20131125.1150.013.html

2013－04－18 网络出版时间：2013-11-25 11:50

国家重点基础研究发展计划（2011CB013703）

任慧龙（1965－），男，教授。研究方向：波浪载荷与结构强度。E-mail：renhuilong＠263.net

翟帅帅（1987－），男，硕士生。研究方向：波浪载荷与结构强度。E-mail：691051190＠qq.com

任慧龙

卢圣芳］