振动压实能力与道路基层材料可压实性评价

王 龙，解晓光

（1.哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨150090）

在现行《公路沥青路面设计规范》（JTG D50—2006）和《公路工程无机结合料稳定材料试验规程》（JTG E51—2009）中，对于无机结合料基层材料的设计，均主张采用振动成型方法，但在振动成型参数上，规定并不十分明确.在振动成型过程中，激振频率、离心力和名义振幅三参数的一种组合形成一套压实工艺，振动三参数对于压实起着关键作用，决定了振动工艺的压实能量；同时，被压材料对振动压实工艺具有反馈特性，其频谱特性、变形特性和加速度特性因材料的不同而不同［1］.不同参数的组合，对振动压实仪来讲，是其输出能量的差别，对被压材料来讲，其反馈的不同是吸收能量的差异.因此，要分析振动压实的机理，推广基层材料振动成型方法，必须对不同工艺的压实能量和不同基层材料吸收振动压实能的状况进行研究，即对振动压实工艺压实能力与被压材料可压实性进行评价，为道路基层材料的振动压实设计和施工控制提供有针对性的技术指导.

1 振动压实仪的动态测试方法

若要对振动压实工艺压实能力和被压材料可压实性进行评价，必须明确各振动压实工艺三参数的能量输入以及各种被压材料的具体反馈数据，因此，对振动压实进行动态测试.测试的内容包括被压基层材料在某一压实工艺下的位移信号、加速度信号和压实力信号.相关测试在自行开发的变频、变幅振动压实仪上进行［2］.

1.1 位移信号的测试方法

基层材料的压实变形采用LVDT（直线位移传感器）进行采集，用磁性表座将位移传感器固定在位移架上，把位移传感器的触头固定在振动压实仪上.位移传感器弹跳的幅度是振动压实仪的实际工作振幅，随着材料逐渐被压实，振动压实仪的重心逐渐下移，位移传感器实测振幅的下包络线为材料随时间变化的塑性变形.

1.2 压实力信号与加速度的测试方法

实际的压实力和离心力在数值上并不相等，压实力必须通过实测才能确定，在圆柱形的压头四周粘贴应变片，组成全桥电路，随着构件受力变形，应变片产生与构件应变成比例的电阻变化，应用测量电路测得应变或应力，进而计算出实际的压实力.加速度的采集采用YD12D－57加速度传感器，将加速度传感器吸附在振动压实仪上，当压实仪的压头与被压材料相接触时，实测的加速度为压实加速；当压实仪的压头与被压材料不相接触时，实测的加速度为空载加速.

2 振动压实工艺压实能力评价

频率、离心力和名义振幅的一个组合称为一个压实工艺，压实工艺不同振动压实效果也存在差别［1］，三参数的关联性说明不能以一个参数来表征压实能力的强弱.压实效果的好坏，是能量的施加与吸收的协调问题，只有采用适合土体吸收能量的压实方式，并达到足够的压实功才能取得好的效果.因此采用工艺的激振强度——单位时间内输出的能量来表征压实能力.

2.1 振动压实工艺的评价参数

根据工程振动理论，利用上表面振动器振动压实时，其理论振动作用力为

式中：P为作用于土体上的竖向力，kN；W为振动压实仪激振部自重，kg；F0为离心力幅值，kN；ω为角频率，rad·s－1；t为时间，s.

若考虑阻尼的影响，则振动压实时试件的竖向位移滞后振动作用力一个相位差φ，每一振动周期内，振动力作正功的时间是t1＝φ/ω到t2＝（π/2＋φ）/ω和t3＝2π/ω到t4＝（2π＋φ）/ω两个时段，故振动器在一个振动周期内的振动压实能为

式中：E0为一个周期内表面振动器施加的能量，J·Hz－1；A为名义振幅，mm；

由于基层材料在压实过程中为弹—塑性状态，φ值不可能为0，但由于采用了分段处理，在最佳激振频率时，试件的振动接近共振状态，此时φ值接近π/2.为计算简便将φ＝π/2代入式（1），则单周期振动器施加的能量为

设激振频率为f，则每秒钟振动压实仪输出的能量为衡量不同压实工艺压实能力的指标——激振强度.由式（2）可知，激振强度E1的计算公式如下：

根据式（3）可知，它综合地反映了振动三参数对理论压实功的影响，物理意义为：单位时间内激振器提供的能量，E1的大小反映了不同压实工艺输出能量的强弱，反映了工艺的压实能力.

2.2 激振强度与基层材料压实性的关系

以3种激振频率（30，45，60Hz）、4种离心力（4，5，6，7kN）、5种振幅、3种级配类型，调制出3×3×4×5＝180个工艺组合，对基层材料（级配碎石）进行压实试验，研究工艺压实能力对基层材料物理指标的影响.

图1是3种结构类型级配碎石材料在激振频率为30，45和60Hz时激振强度与干密度散点图.3种级配的干密度随激振强度的提高而增长，但变化规律不同，其中，各级配干密度的最大、最小值及离散性反映了级配的骨架—空隙、骨架—密实和悬浮—密实的差异（内因），而干密度随激振强度的变化则体现了压实工艺的影响（外因）.对细级配来说，由于最大粒径较小以及悬浮结构，干密度增长率较小，单位激振强度为0.05g，且离散性最小.对中级配来说，干密度随激振强度的增长呈对数分布，增长率大，单位激振强度为0.09g，离散性也大.说明虽是好的级配类型也必须采用合适的振动参数组合才能取得好的压实效果.粗级配散点的走势与中级配相同，由于是骨架—空隙型结构，其干密度较小，增长率为单位激振强度0.09g.纵观3幅图的总体走向，干密度的增长率在激振强度为0.2kJ·s－1时出现转折，小于0.2kJ·s－1时平均增长率为单位激振强度0.2g，大于0.2kJ·s－1时平均增长率为单位激振强度0.02g.说明工艺的激振强度必须突破0.2 kJ·s－1的阈值，干密度的增长才进入稳定状态.同时还可以看出，要想取得良好的压实效果，激振强度必须大于0.35kJ·s－1.

图1 不同频率下激振强度与干密度的关系Fig.1 Relationship between vibration strength and dry density at different frequencies

图2为激振强度与名义振幅的关系图.可以看出，名义振幅与激振强度具有线性关系，根据激振强度，可以确定各压实工艺的压实能力，根据前面总结出的激振强度的阈值，确定出最佳工艺区间，最佳工艺区间激振强度必须大于0.35kJ·s－1，此时，工艺要求为激振频率为30Hz，离心力大于6kN，名义振幅大于0.64mm；在次佳工艺区间，激振强度要求大于0.2kJ·s－1，此时要求离心力大于6kN，频率可为30Hz或45Hz，名义振幅大于0.6mm.

图2 不同工艺组合名义振幅与激振强度关系图Fig.2 Relationship between nominal amplitude and vibration intensity with different processes

3 道路基层材料可压实性评价

振动压实工艺压实能力与道路基层材料可压实性是一个问题的两个方面，前者是输入，后者为反馈，采用振动压实并采集被压材料的塑性变形、压实力等反馈数据后，才能实现对其可压实性的评价.

3.1 塑性变形回归分析

振动工艺提供的能量并不等于试件吸收的能量，基层材料吸收能量主要用于产生塑性变形，因此评价被压材料的可压实性，需分析被压材料的塑性变形曲线特性.图3为实测被压材料的变形随时间的变化曲线.图4为经过换算后得到的压实过程中材料的压实度随时间的变化曲线.可以看出，在振动作用下，基层材料的塑性变形曲线和压实度增长曲线与振动时间的关系为对数关系［3］.

图3 水稳碎石基层材料塑性变形随时间变化曲线Fig.3 Curves of plastic deformation with time of cement stable macadam

从图3中可以看出，随着压实时间的增加，被压实材料的塑性变形逐渐增加.在压实的前20s，材料的变形速率很大，变形量为总变形量的50%左右，随着材料逐渐被压实，变形速率随之减小并达到稳定［4］.从图4中可以看出，试样的装填压实度为80%，压实的初期，压实度增幅较快，在50s后压实度达到了95%，100s后达到了98%，200s后达到了100%.通过实测到的位移响应信号，可以直接反映成型过程中材料的压实情况和不同材料在压实过程中的变形特性.

图4 水稳碎石基层材料压实度随时间变化曲线Fig.4 Curves of compaction degree variation with time of cement stable macadam

图5是不同道路基层材料在压实过程中的塑性变形曲线，石灰稳定碎石的总塑性变形最小，而二灰结合料的总变形最大，塑性总变形的不同说明了各种材料初始密实程度的不同；曲线的前期，由于材料的塑性变形比较大，材料的变形速率不是常数，在振动压实前40～50s，塑性变形已经达到了其总变形量的50%左右.当50s后材料的变形相对稳定，随着材料逐渐被压实，材料的变形速率为一常数；把不同材料的变形曲线进行对数回归，回归方程中系数的绝对值越大，材料变形的速率越快，由于有初始状态的影响，并不能以此评价不同材料的可压实性.由于50s以后，材料的变形逐渐稳定，对50s以后的数据进行线性回归分析，根据回归方程的斜率k，计算产生单位变形时所需要的时间［5］.用此指标评价不同材料的可压实特性，回归数据如表1，对于沥青混合料中，k＝26s·mm－1，表示材料产成1mm变形所需要的时间是26s；k值越大，材料产生单位变形所需要的时间越多，材料越不易被压实.

图5 不同基层材料振动压实塑性变形曲线Fig.5 Curves of vibrating compaction plastic deformation curve of different base materials

表1 不同道路材料压实稳定状态下塑性变形回归方程Tab.1 Plastic deformation regression equation of different road materials compaction stability states

3.2 基层材料可压实性评价指标

虽然塑性变形曲线可以直观地反映材料在压实过程中的变形特性［6－7］，但是用塑性变形去评价被压材料的可压实性有局限性.原因是压实力的监测表明不同材料在压实过程中，受到的实际压实力是不同的，而材料的塑性变形与压实力直接相关.因此需要综合考虑压实力和位移指标来评价材料的可压实特性，由于试件尺寸的差别，把试件受到的实际压实力转换成了压实应力.

根据塑性变形随时间的变化曲线，当压实时间t＞50s后，材料的位移曲线近似为一直线，定义可压实性系数L，其物理意义为材料产生单位塑性变形所需的压实应力，计算公式如下：

式中：L为材料可压实性系数，MPa·mm－1；d为材料产生单位位移所需的时间，s·mm－1；n为单位时间压实次数，次·s－1；σ为平均每次的压实应力，MPa·次－1.

就沥青混合料而言，可压实性L值计算方法如下：L＝26s·mm－1×10次·s－1×2.98MPa·次－1＝773.73MPa·mm－1.表2为振动压实最佳工艺下不同材料的可压实性指标计算结果.可压实系数越大，产生单位塑性变形所需的压实应力也愈大，可压实性就越差.

利用产生单位位移所需的压实应力作为评价材料可压实特性的指标，此指标综合考虑了材料在振动压实的过程中，材料的变形速率、振动压实次数和振动压实应力的综合因素.从表2中可以看到沥青混合料产生单位变形所需的应力要远大于其他材料，二灰结合料可压实性最好，水泥稳定碎石和粉煤灰稳定碎石基本处于同一水平，石灰稳定碎石和二灰结合料的可压实性处于同一水平.

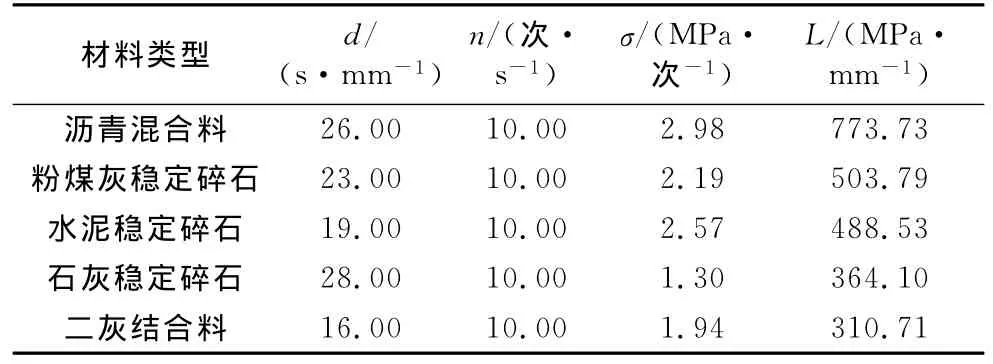
表2 不同道路材料压实特性指标Tab.2 Compactibility indexes of different road materials

4 结论

（1）对不同参数组合下的振动压实工艺单位时间内输出的能量进行了分析，定义了评价振动压实工艺压实能力的评价指标.

（2）对于压实效果的影响，激振强度存在阈值，激振强度必须大于0.35kJ·s－1才能取得良好的压实效果；根据名义振幅与激振强度的关系，提出了最佳振动压实工艺区的范围.

（3）道路材料的振动压实塑性变形和压实度的变化与振动时间呈对数关系.

（4）定义了道路材料可压实性参数，不同道路材料的可压实性系数具有较大的区别，说明采用可压实性参数能区分不同道路材料的可压实性，具有一定的合理性.

［1］ WANG Chunming，XU Shifa，LI Ping.Aggregate gradation optimization design of cement stabilized aggregate and effects of molding methods on test results［J］.Journal of Beijing University of Civil Engineering and Architecture，2007，23（3）：15.

［2］ 王龙，解晓光.级配碎石材料标准振动成型方法的研究［J］.公路交通科技，2005，22（7）：26.WANG Long，XIE Xiaoguang，Research on the vibrating compaction method of graded aggregate material［J］.Journal of Highway and Transportation Research and Development，2005，22（7）：26.

［3］ 王红.道渣弹性与累计变形的试验研究［J］.中国铁道科学，2001，22（6）：106.WANG Hong.Test and study on ballast elasticity and accumulated deformation［J］.China Railway Science，22（6）：106.

［4］ 王龙，解晓光，冯德成.级配碎石材料强度及塑性变形特性［J］.哈尔滨工业大学学报，2007，39（6）：944.WANG Long，XIE Xiaoguang，FENG Decheng.Characteristics of the modulus and plastic deformation of the graded aggregate material［J］.Journal of Harbin Institute Technology，2007，39（6）：944.

［5］ 杨人凤，张永新，杨云岭.冲击振动联合作用下土的压实机理试验［J］.长安大学学报：自然科学版，2003，23（3）：64.YANG Renfeng，ZHANG Yongxin，YANG Yunling.Test for soil compaction principle by impaction and vibration［J］.Journal of Chang＇an University：Natural Science Edition，2003，23（3）：64.

［6］ 刘本学，冯忠绪，赵侃，等.仿冲击振动压实机动力学模型的建立及压实试验［J］.中国公路学报，2007，20（3）：121.LIU Benxue，FENG Zhongxu，ZHAO Kan，et al.Establishment and compaction experiment of dynamics model for impaction vibratory roller［J］.China Journal of Highway and Transport，2007，20（3）：121.

［7］ WANG Long，XIE Xiaoguang.Influences of laboratory compaction methods on shear performance of graded crushed stone［J］.Journal of Materials in Civil Engineering，ASCE，2011（10）：1483.