动态车辆路径问题的隐分区灵活分批策略
熊 浩,符 卓,鄢慧丽
(1.中南大学 交通运输工程学院,湖南 长沙410083;2.长沙理工大学 交通运输工程学院,湖南 长沙410004)
Psaraftis[1-2]最 早 提 出 了 动 态 旅 行 商 问 题(dynamic vehicle routing problem,DVRP),并 将DVRP定义为“安排车辆路径以满足实时出行的顾客需求”.后来,Bertsimas等[3-5]利用排队理论进行策略有效性分析和设计,提出了多种优化策略.Pillac等[6]对动态车辆路径问题进行了综述,首先将动态车辆路径问题分为动态确定性问题和动态随机性问题.动态确定性问题的方法分为精确算法和启发式策略,分别包括基于线性规划的滚动优化法[7]、动态列生成算法[8]和基于场景的计划法[9]、动态蚁群算法[10]等;动态随机性问题的方法主要有Sampling策略[9]等.
20世纪90年代后期在计算机技术发展后,动态需求车辆路径问题虽然逐渐得到了重视,但是相关研究注重以算法设计为主,其策略研究反而被忽略了.目前相对较好的策略是分区定量旅行商策略或分区定时旅行商策略[3-5],且这2种策略的有效性相同,所以一般可以把这2种策略合称为分区分批旅行商策略.但是该策略的有效性离理想状态的效果仍有较大差距,是理想状态的策略下界值的11倍[3-5].可见,密集需求的实时优化策略仍然有很大的进一步探索改进空间.
因此,本文在分区分批旅行商策略的基础上提出了一种新的策略——隐分区灵活分批旅行商策略.该策略利用虚拟区域进行扫描分区,并且允许在排队等候时分区中新出现的顾客进入决策,并保证优化路径中的顾客数与进入队列时顾客群的顾客数保持一致.对这种新策略的有效性分析表明,新策略能在不改变顾客群排队时间的情况下减少车辆平均行驶距离和顾客群形成时间,从而使平均系统时间减少.最后对该策略进行了仿真分析,结果表明了灵活分批旅行商策略相对于一般分批旅行商策略有较大的改进.
1 问题描述
本文的动态车辆路径问题是指完全动态需求车辆路径问题.完全动态需求是指动态出现的顾客要求响应时间为零的车辆路径问题,即顾客希望从呼叫到被服务的时间为零.该类问题在优化的时候以追求响应时间最短为唯一目标,尽量减少顾客等待时间.常见的动态旅行商问题(dynamic traveling salesman problem,DTSP)、动 态 修 理 员 问 题(dynamic traveling repairing problem,DTRP)等都属于完全动态需求车辆路径问题.准动态需求问题是指动态出现的顾客对响应时间有一定的容忍范围,允许在一定的时间范围之内接受服务的车辆路径问题.根据响应时间的时间范围不同可以分为带时间窗的动态需求车辆路径问题和多阶段动态车辆路径问题.前者给出最早可以开始服务的时间和最晚必须服务的时间,后者只有最晚必须服务时间.该类顾客因为有提前呼叫的时间段,所以运营商有时间进行合理安排,所以这类问题一般以车辆路径最短或服务的顾客最多为主要目标.
完全动态车辆调度问题包括:动态旅行商问题、动态修理员旅行问题和在线旅行商问题(online travelling salesman problem,OLTSP).其中,动态旅行商问题和动态修理员问题几乎是同一类问题,是指修理员或车辆需要服务随时间动态出现的顾客需求,目标是使期望系统时间最少.顾客需求产生过程的时间符合以分布密度为λ的泊松分布,且独立分布在某个区域A;车辆从车场出发以固定的速度去服务这些顾客,在每个顾客节点的服务时间为t0,节点i和节点j之间的距离为tij,该问题需要销售商寻找最优的路径去服务这些需求,使每个顾客的平均系统时间最少.系统时间是每个顾客从其出现在系统中到服务被完成所必须花费的平均时间,包括等待时间和在线服务时间.利用顾客出现过程的时间分布和地理位置分布寻找最优的策略使系统时间最少.
2 隐分区灵活分批旅行商策略
2.1 策略概述
隐分区策略是指在静态子问题形成规则上做一些区域范围的规定.区域中的分区并不固定,而是按照一定的规则灵活确定,满足被计划的顾客处在一定区域范围内,从而保证旅行商平均距离较短.隐分区策略又分为隐分区定量策略和隐分区定时策略.
隐分区策略利用普通分区策略的基本思路,保证制定计划的顾客路径始终发生在一定的区域内,从而同样保证了路径的平均距离较短;并且由于是隐分区,所以顾客群组形成时间更短,从而缩短了平均系统时间.因此,与普通分区策略相比,其队列形成时间变短,群组在队列中的排队时间不变,群组服务时间不变,群组的服务过程中的路径时间不变.从而隐分区策略能够使顾客的平均系统时间变短.
(1)隐分区定量策略.将区域分割成k个分区,则隐分区的范围为2π/k.在区域中构建2条射线夹角为2π/k的扇形,以该扇形进行扫描搜索,当扇形覆盖区域的顾客数大于等于n(定量策略的批量)时,该被覆盖区域构成的分区进入队列,见图1a.
(2)隐分区定时策略.将区域分割成k个分区,则隐分区的范围为2π/k.在区域中构建2条射线夹角为2π/k的扇形,每隔固定时间T,以该扇形对整个区域进行扫描搜索,统计所有被扇形覆盖区域中顾客数量,被覆盖区域顾客最多的区域被锁定并进入队列,见图1b.
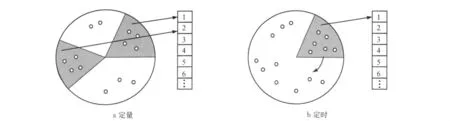
图1 隐分区灵活定量与定时策略排队情况Fig.1 The queuing of the virtual partition and flexible time batch TSP strategy
(3)灵活分批策略.灵活分批策略是对分区分批策略做了一些调整而形成的策略.假设分区进入队列的时间为T1,车辆空闲的时间为T2,计划优化计算需要时间为Δt,则开始决策时间为T3=max{T1,(T2-Δt)}.当决策的时间为T2-Δt时,则T1~(T2-Δt)时间内出现的新顾客也会进入决策范围,从而使顾客数大于定量策略的批量n或定时策略的顾客批量N.
2.2 有效性分析
隐分区定量旅行商策略与普通分区定量旅行商策略相比,不再以固定的分区统计顾客数量,而是任意夹角为2π/k的区域中顾客数达到n个时该区域被锁定进入队列.该策略不改变顾客的平均服务等待时间,不改变顾客群排队时间.由于队列仍然符合顾客到达时间间隔是一般分布和服务时间也为一般分布的G/G/m排队模型条件[4],且相关参数都没有改变,所以分区排队时间不变,但是顾客群形成时间可能会缩短,因为原固定分区边界附近属于不同分区的顾客按照隐分区策略只要达到n个也可以进入队列,而原分区策略则仍然需要等待.
同样,隐分区定时旅行商策略与普通分区定时策略相比,不再是以固定间隔期的扫描时间确定进入队列,而是在固定的时间间隔内,只要夹角为2π/k的区域中顾客数最多,则该区域被锁定并进入队列.该策略不改变分区顾客群形成时间和顾客群排队时间(由于队列仍然符合顾客到达时间间隔是固定值和服务时间为一般分布的D/G/m排队模型条件,排队时间的相关参数不变,所以分区排队时间不变);该策略能使同等时间内分区中的顾客数量增加,则分摊到单个顾客的形成时间、排队时间减少;且更多顾客构成的路径平均距离缩短;而单个顾客的服务时间固定不变;因此,隐分区灵活定时策略的平均系统时间明显减少.
另外,隐分区灵活定量策略与隐分区非灵活定量策略相比,在隐分区内进行不同群组中顾客的交换优化要确保不影响群组形成时间.当某个隐分区出现n个顾客时,按照规则对出现时间点和车辆空闲时间进行比较,若车辆空闲时间较晚则需要等待.由于等待可能会出现新的顾客,这时灵活分批要求将所有已经出现顾客加入决策系统进行“择优选择”.通过择优减少路径时间,从而减少顾客系统时间.但是,择优选择可能会使后来出现的顾客被安排进入执行计划,从而使非灵活分批策略的顾客发生了变化,数量不变但是位置发生了改变,所以对后续的隐分区的形成时间有一定影响,该影响比较随机而难以判断.
同理,隐分区灵活定时策略与隐分区非灵活定时策略相比,在隐分区内进行不同群组中顾客的交换优化不影响群组顾客的平均数量,需要事先统计隐分区的顾客数量,以保证灵活分批后的顾客数量仍然保持不变,以确保不影响群组形成时间而不改变排队模型.但是,同样由于择优选择会影响顾客的位置,所以对后续的隐分区的形成时间有一定影响.
2.3 策略构建
2.3.1 隐分区灵活定量旅行商策略
整个区域的顾客数达到n时以夹角为θ0的扇面开始扫描,判断是否有n个顾客落在该扇面之内,若没有,继续等待新的顾客出现直至以夹角为θ0的扇面能够扫描,使落在该扇面内的顾客数为n,该n个顾客中以极坐标角度θ1~θ2之间的扇面区域进入队列,其中θ1为最小值,θ2=θ1+θ0.
2.3.2 隐分区灵活定时旅行商策略
每隔T0时间以夹角为θ0的扇面开始扫描,统计扇面内顾客的数量和扇面的位置,扇面内顾客数最多的区域进入队列排队.统计这时分区中的顾客数N,该区域为以其中顾客极坐标角度为θ1~θ2的扇面区域.
2.3.3 灵活分批策略
实时优化策略决策输入要素为顾客和车辆,其确定方法如图2所示,其中T3为决策时间;T4为计划分派时间;T′3为上次决策时间;T′4为上次计划分派时间.

图2 静态子问题的输入信息Fig.2 The input information of the static sub-problem
(1)静态子问题的顾客群包括上次计划时剩下未被服务的顾客和新出现的顾客.若用C表示在T4时上次计划时剩下未被服务的顾客,Q表示在[T′3,T3]期间新出现的顾客,则在T3时进入决策的顾客为N′,N′=C∪Q.并且,静态子问题的优化决策需要从顾客群N′中挑选最优的n或N个顾客构成新的路径计划.
(2)静态子问题的车辆包括正在执行路径计划的车辆和在车场等待的车辆.首先可以根据路径计划计算出在新的决策时刻执行完路径计划的可用车辆为U1;然后考虑决策时仍然在车场闲置的车辆U0,则所有可用的车辆为V=U1+U0;最后从这些车辆中挑选合理的车辆进行路径计划.
3 实例仿真
3.1 仿真步骤
(1)设置策略参数:区域分区数量k,隐分区的角度θ0=2π/k;区域分批的顾客数量n或定时的时间间隔T.
(2)生成顾客;随机生成顾客位置在均匀分布的圆形区域,取原点为圆心;随机生成到达时间间隔为负指数分布,累计构成顾客的随机到达时间,则该过程符合泊松过程.按照一定的条件设置参数:服务强度趋向于1,即服务时间与单位时间到达顾客个数之积趋近于1(多车辆需要除以车辆数);一般区域半径时间距离大于顾客服务时间(说明距离对系统时间影响较大,且符合实际情况).一般限定顾客的总数量或者仿真时间长度.
(3)隐分区灵活定量旅行商策略的主循环包括以下三方面的主要内容.①首先,利用扇形区域进行扫描,寻找满足条件的区域.对于定量分批:统计区域中剩余未被安排计划的顾客数量,当整个区域中的顾客数量超过n时,开始隐分区扫描,若这n个顾客构成的区域最小夹角大于θ,则需继续等待新的顾客出现,每出现1位顾客,扫描1次,直到n+Nt个(Nt表示前n个顾客之后出现的顾客数量),此时n+Nt顾客中至少有n个顾客构成的夹角小于等于θ.对于定时分批:在每个定时时间间隔点统计各种可能的隐分区的顾客数量,按照当前系统中的顾客的角度从小到大排序,从系统中顾客角度最小的顾客开始扫描θ0,记录该分区中的顾客数;然后依次从第2位顾客开始扫描θ0,记录该分区中的顾客数;直到最后1位顾客再扫描θ0.记录所有隐分区中顾客数量(假设为N,每个定时间隔点可能都不同)最大的隐分区的开始角度θ1和结束角度θ2.②比较进入队列时间和车辆空闲时间,确定决策开始时间;根据该时间统计上一步确定的分区内的顾客数量,进行路径优化分派.路径优化的方法可以采用不同的智能启发式算法:遗传算法、蚁群算法、粒子群算法等,本文选用遗传算法.③对仿真期间剩余顾客进行更新,删除已分派的顾客.
(4)循环结束条件:区域中剩余的顾客不能满足分区进入队列条件.
3.2 实例
设置1组数据进行仿真:区域范围的半径为r=10,车辆数量为m=5,顾客到达的时间符合泊松分布且平均值为λ=10,服务时间为s=1;设置策略参数:k=10,n=10或T=20和计算时间Δt=0.5,分别采用隐分区定量旅行商策略和隐分区灵活定量旅行商策略进行仿真,结果如表1所示.该结果表明:隐分区灵活定量旅行商策略由于可以较大幅度地降低路径长度,从而使顾客的平均系统时间有所缩短.

表1 隐分区定量与隐分区灵活定量旅行商策略仿真结果Tab.1 Results of the simulation on the flexible and the non-flexible quantity batch strategies
利用该参数重新生成另外1组顾客,分别采用隐分区定时旅行商策略和隐分区灵活定时旅行商策略进行仿真,结果如表2所示.该结果显示:隐分区灵活定时旅行商策略由于可以减少平均路径长度,从而使顾客平均系统时间也有所减少.

表2 隐分区定时与隐分区灵活定时旅行商策略仿真结果Tab.2 Results of the simulation on the flexible and the non-flexible time-batch strategies
4 结论
隐分区灵活分批旅行商策略分为隐分区灵活定量旅行商策略和隐分区灵活定时旅行商策略.相对于一般分区分批旅行商策略而言,新策略主要从2个方面做了改进:①通过设置虚拟分区,保持了分区顾客的到达率不变,使顾客群的形成时间减少;②对决策时间进行了调整,允许在顾客群形成时间与开始决策时间内出现的新顾客进入决策,使进入计划的顾客更多,从而使路径平均距离更短.仿真分析结果也证明了新策略能够使路径距离变短,从而使平均系统时间减少.
[1] Psaraftis H N.Dynamic vehicle routing:status and prospects[J].Annals of Operations Research,1995,61(1):143.
[2] Psaraftis H N.Dynamic vehicle routing problems[M].North-Holland:Elsevier Science Publishers B V,1988.
[3] Bertsimas D J,Van Ryzin G.Stochastic and dynamic vehicle routing with general demand and interarrival time distributions[J].Advances in Applied Probability,1993,25(4):947.
[4] Bertsimas D J,Van Ryzin G.Stochastic and dynamic vehicle routing in the Euclidean plane with multiple capacitated vehicles[J].Operations Research,1993,41(1):60.
[5] Bertsimas D J,Van Ryzin G.A stochastic and dynamic vehicle routing problem in the Euclidean plane[J].Operations Research,1991,39(4):601.
[6] Pillac V,Gendreau M,Guéret C,et al.A review of dynamic vehicle routing problems[J].European Journal of Operational Research,2013,225(1):1.
[7] Yang J,Jaillet P,Mahmassani H.Real-time multivehicle truckload pickup and delivery problems[J].Transportation Science,2004,38(2):135.
[8] Chen Z L,Xu H.Dynamic column generation for dynamic vehicle routing with time windows[J]. Transportation Science,2006,40(1):74.
[9] Bent R W,Van Hentenryck P.Scenario-based planning for partially dynamic vehicle routing with stochastic customers[J].Operations Research,2004:977.
[10] Montemanni R,Gambardella L M,Rizzoli A E,et al.Ant colony system for a dynamic vehicle routing problem[J].Journal of Combinatorial Optimization,2005,10(4):327.

