基于管段重要性的给水管网布局分析

李树平，周巍巍，侯玉栋，黄 璐

（同济大学 环境科学与工程学院，上海200092）

给水管网包含两种基本布置形式：树状网和环状网.通常认为树状网的供水可靠性较差；管网中任一管段损坏时，该管段以后的所有管线就会断水，得不到服务.而环状管网中，管线连接成环；直观上认为任意管段损坏时，水还可从另外管线供应用户，可以缩小断水区域，从而增加供水可靠性［1－2］.事实上如果引入给水管网冗余，即备选路径配水能力的概念，将会发现当由连通管将树状管网形成环状管网时，如果供水压力不是很充分，很可能出现仅具有连通性（即从水源到某一节点具有不同的连通路径）冗余，而没有提高能力（管段的过水能力）冗余.

给水管网设计计算中，除按设计年限内最高日最高时的用水量决定管道直径和水泵尺寸外，还应进行事故工况校核.即按最不利管段损坏而断水检修的条件，核算事故时的流量（按最高日最高时用水量的70%）和水压是否满足要求.当靠近水源处具有两条以上不同方向的管道时，最不利管段的选择通常根据主观经验确定.

城市供水安全管理中，常常按照供水事故影响用水程度和紧急程序进行分级.例如某市将供水事故分为四级，其中I级为特别重大事故，供水范围内有三分之二用户无供水；II级为重大事故，供水范围内二分之一无供水；III级为较大事故，供水范围内三分之一用户无供水；IV级为一般事故，局部地区用户无供水.因此需要考虑管网内管道处于什么样的状况，才能出现不同程度的供水分级情况.

以上给水管网规划、设计和运行管理中遇到的问题，即在管段出现故障下，判断能否满足用户用水需求，以及满足用户的供水比例有多少.是否满足用户用水需求，可采用给水管网水力模型分析计算；而判断管道发生故障后所引起的供水服务降低程度，需要引入管段重要性的概念.管段重要性（LIi）可定义为当管段i出现故障时，难以提供的需水量（Fi）占总需水量（D）的比例，即［3］

管段重要性可以作为管段在整个管网中关键程度的相对性衡量：LI数值较高的管段断开时，它对管网供水的影响较大；LI数值较低的管段断开时，对管网供水的影响较小.

针对管段重要性判断的实际需求，从构造不同给水管网布局方案出发，结合水力计算和管段重要性评价，探讨管网布局的规律和特点.管网图中，若干管段顺序连接时称为管线，起点与终点重合的管线构成环.在一个环中，不包含其他环时，称为基环.

1 构建基本管网案例

示例给水管网（图1）取自文献［4］，图中编号中J表示节点，L表示管段；在文献中用于研究不同管网布局的可靠性和置信度.该管网基本布局为树状网，含有11条管段、11个连接节点、1个水源节点.图1中的虚线将在后续各种环状网布局方案中作为连通管段引入.图中节点地面标高和需水量见表1，所有节点需要的最低服务水头为20m.假设所有管段（含连通管段）长度均为400m，管段水头损失采用海曾 威廉公式计算，所有管道的粗糙系数C值取100.各管段直径见表2.水源（节点R1）的总水头为H1＝80m.

图1 给水管网示意图Fig.1 Schematic diagram of water distribution system

表1 节点地面标高和需水量Tab.1 Nodal elevations and demands

表2 管道直径Tab.2 Pipe diameters

管段重要性采用式（1）计算；假设当不满足节点最低服务水头时，该节点供水量为零.分析中采用Epanet软件执行水力计算，它是由美国环保局开发，可以执行有压管网水力和水质特性延时模拟的计算机程序；为求解给定时间点管网水力状态的流量连续性和水头损失方程组，使用的方法称作梯度方法或混合节点 环方法［5］.

2 给水管网布局分析

给水管网布局分析将分5种情况讨论：①单环路管网情况；②多环路管网情况；③增加贮水池供水压力情况；④改变连通管道直径情况；⑤管网中添加另一水源情况.

2.1 单环路管网

树状管网中不同位置添加连通管道，形成了各种单环路管网.本组分6种方案讨论：方案a，不含环路的管网，即树状网；方案b，添加连通管段L12，管径250mm；方案c，添加连通管段L13，管径200 mm；方案d，添加连通管段L14，管径200mm；方案e，添加连通管段L15，管径200mm；方案f，添加连通管段L16，管径200mm.

经计算，各方案的管段重要性见表3和图2.因为方案a的水力计算结果满足各节点需水量和水压要求，所以当方案b～方案f中去除各连通管段时，不影响管网的供水能力，故按照管段重要性定义，这些连通管段的管段重要性均为零，故在各种方案讨论图表中未列出.

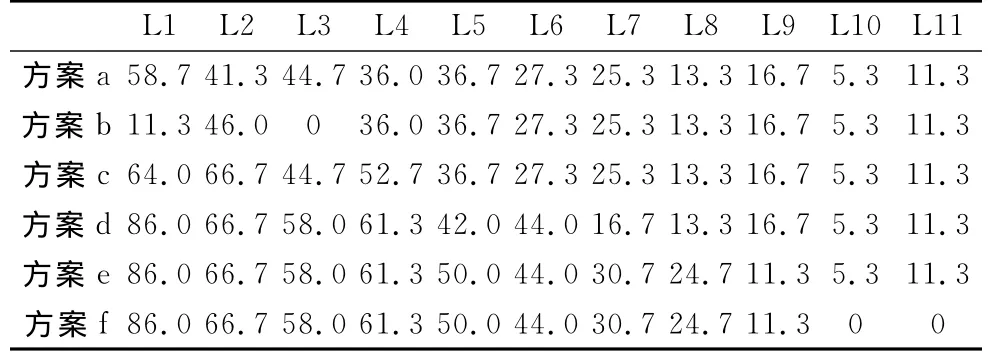
表3 单环路管网各方案的管段重要性Tab.3 Link importance indicators of single loop networks %

由表3和图2可以看出：①树状管网方案a中，服务用水量多的管段与服务用水量少的管段相比，管段重要性要高；②方案a添加连通管段L12后，形成方案b，成环部分管段重要性发生显著变化，原L1管段重要性由58.7%降至11.3%；L2管段重要性由41.3%增至46.0%，L3管段重要性由44.7%降至零；③方案b、方案c和方案d相比，不同位置添加连通管段时，随着环路内管段数的增多，成环各管段的重要性增加；④方案e与方案d相比，成环管段L7和L8的管段重要性增加，但L9的管段重要性降低；⑤方案f与方案e相比，除成环管段L10和L11的重要性降低为零外，其余管段的重要性数值相同.

图2 单环路管网各方案的管段重要性Fig.2 Link importance indicators of single loop networks

2.2 多环路管网

树状管网的基础上添加更多的连通管道，形成了含多个基环的管网.本组给水管网布局分析分以下5种方案讨论：方案g，添加连通管段L12（管径250mm）和 L13（200mm）；方案h，添加连通管段L15（200mm）和L16（200mm）；方案i，添加连通管段L12、L13和L14（200mm）；方案j，添加连通管段L14、L15和L16；方案k，添加连通管段L12—L16，共含5个基环.

经计算，各方案的管段重要性列于表4.图3将方案a、b、g、i、k进行图示比较，特点是从无环、单环到多环，环中所含管段依次增加.图4将方案a、f、h、j、k进行图示比较，特点同样是从无环、单环到多环；与图3不同的是，随着基环的增加，环内所含管段数保持不变.

表4 多环路管网各方案的管段重要性Tab.4 Link importance indicators of multi－loop networks %

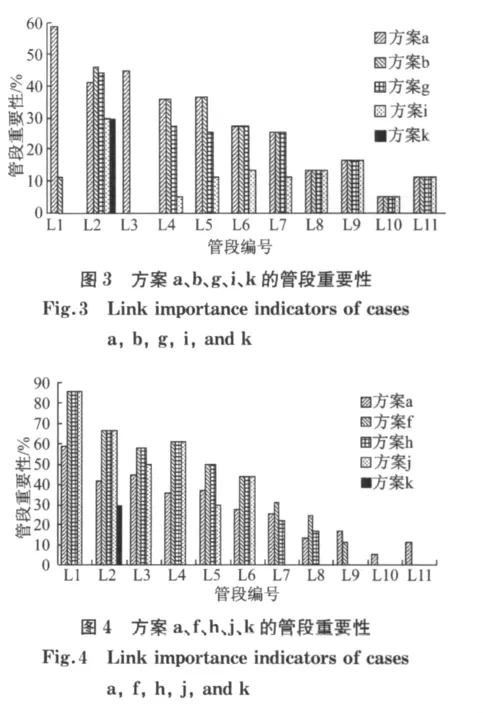
由图3可以看出，随着方案a、b、g、i和k中基环数的增加，环内所含管段的重要性依次降低.由图4看出，方案f、h、j、k中成环管段数未变；但随着基环数量的增加，可知：靠近添加连通管段处的管段重要性降低，而远离连通管段处的管段重要性受环数增加的影响较小，该特性可称作连通管段的局部效应，即管段数量较少（总管长较小）的基环内部某条管段断开，对整个管网供水影响较小；管段重要性为零的情况依次增多.

2.3 管网供水总压力增大情况

本组方案将探讨管段重要性对管网供水压力增大后的敏感性.选取管网布局方案a1、d1、f1和k1，分别对应于方案a、d、f和k；水源（节点R1）的总水头由原来的H1＝80m提高到H1＝90m.经计算，各方案的管段重要性见表5.

表5 管网供水压力增加后的管段重要性Tab.5 Link importance indicators with the water pressure being increased %

结合表3—5，可以看出：①方案a1与方案a相比，因为树状管网内各节点需水量未变，且在H1＝80m条件下就可以满足供水管网水力需求，供水管网总压力升高后同样可以满足需求，且各管段流量不变，因此相应的管段重要性未发生变化；②环状管网方案d1、f1、k1分别与方案d、f、k比较，随着供水压力的变化，环内各管段存在流量重新分配的问题，因此成环部分管段重要性发生了变化；随着供水压力的提高，具有多个方向来水的节点需水量在一条管段断开时，更加有机会得以满足，因此成环部分管段重要性降低，管网总体供水可靠性提高.

2.4 连通管段直径变化情况

本组管网布局方案用于探讨管段重要性指标对连通管段直径变化的敏感性.选取方案c2、d2、e2和f2，分别对应于方案c、d、e和f；各方案中所有连通管段（L13—L16）的直径改为100mm.经计算，各方案的管段重要性见表6.

表6 连通管段直径为100mm时的管段重要性Tab.6 Link importance indicators with connecting pipe diameter of 100mm %

结合表3和表6，将方案c2、d2、e2、f2分别与方案c、d、e、f比较，可以看出当连通管段直径由大变小后，与连通管段相邻的部分管段重要性增大，而其他管段重要性数值受到影响较小；同样可以看作连通管段的局部效应，即因为连通管段长度较短，在各种流量下引起的水头损失在整个管网中所占比重较小.

2.5 添加新水源

在节点J12处新增一处水源，供水水位H12＝85 m，选取方案a3、f3和k3，分别对应于方案a、f和k，考察管段重要性变化情况.经计算，各方案的管段重要性见表7.

表7 双水源供水情况下各方案的管段重要性Tab.7 Link importance indicators with dual－source water supply %

结合表3、表4和表7，可以看出：

（1）尽管方案a3和a的管网布局为树状管网，节点J2，J4，J6，J8，J10和J12满足双向、双水源供水，与这些节点相连的单条管段断开，仍可满足节点需水量，因此L1，L3，L5，L7，L9，L11的管段重要性均降至零.但对于单向供水的节点J3，J5，J7，J9和J11，当与其相连管段断开后，需水量满足情况与方案a相同，因此L2，L4，L6，L8，L10的管段重要性不变.因此可以得出，当树状管网由单水源改为多水源供水时，能够通过多向、多水源供水的节点，与其相连的管段重要性降低；而单向供水的节点，与其相连的管段重要性没有受到影响.

（2）方案f3和方案k3中各管段的重要性均为零.说明当环状管网由单水源改为多水源供水时，由于管网内环路影响，节点通过双水源供水的可能性提高，与其相连的管段重要性降低.

3 结束语

管段重要性作为管段在整个管网中关键程度的相对性衡量，在给水管网规划、设计和运行管理中具有重要作用，便于及时判断并关注重要性高的关键管段.

树状管网从水源到每一需水节点仅存在一条输水路径，无连通性冗余和能力冗余，当某管段出现故障后，其下游需水节点均受到影响，因此具有高供水能力要求的上游管段重要性要比具有低供水能力要求的下游管段重要性高.

通过添加连通管，树状管网形成环状管网后，随即出现连通性冗余，但能力冗余将取决于整体布局：

（1）当添加连通管道成环后，连通管段所在基环内的各管段重要性受到影响，但重要性数值升高或者降低需进一步确定；

（2）环状管网基环数目依次增多时，即存在连通管段的局部效应；在所添加连通管道附近的管段重要性受到影响，但远离小环部分的管段重要性未受影响；

（3）随着供水压力的升高，成环部分各管段重要性下降，管网的能力冗余提高；

（4）当连通管道的管径由大变小时，连通管段同样存在局部效应，即与连通管道相邻的管段重要性受到影响（由小变大），其余管段重要性受影响较小.

当管网由单水源改为多水源供水时，管网中管段的重要性显著降低，管网供水可靠性明显提高.

（1）对于枝状管网，具有多方向、多水源供水的节点，与其相连的管段重要性降低；而单向供水的节点，与其相连的管段重要性没有受到影响；

（2）对于环状管网，由于管网内环路影响，节点通过双向供水的可能性提高，与节点相连的管段重要性降低.

基于本研究，提出以下建议：

（1）给水管网的正常功能需要从结构、水力和水质三方面分析，因此管段重要性评价不仅仅体现对水力特性的衡量，也应探讨并体现结构和水质方面的特性；

（2）给水管网水力分析采用了基于需水量的模型，即管网分析中通常认为用户需水量是与管网供水压力无关的；事实上，当管网压力低于特定临界水平时，仍可能具有一定的水量输送到用户，因此如果采用基于压力的管网模型，计算结果可能更具有现实意义；

（3）真实给水管网的拓扑结构、供水模式等方面更加复杂，因此需要利用更多的管网实例进行分析，便于提出更具有指导意义的管段重要性理论.

［1］ 严煦世，刘遂庆.给水排水管网系统［M］.2版.北京：中国建筑工业出版社，2008.YAN Xushi，LIU Suiqing.Water distribution and drainage systems［M］.2nd ed.Beijing：China Architecture and Building Press，2008.

［2］ 李树平，刘遂庆.城市给水管网系统［M］.北京：中国建筑工业出版社，2012.LI Shuping，LIU Suiqing.Urban water distribution system［M］.Beijing：China Architecture and Building Press，2012.

［3］ Goulter I，Walski T M，Mays L W，et al.Reliability analysis for design［C］//Water Distribution Systems Handbook.New York：McGraw－Hill Companies Inc，2000：18.1－18.52.

［4］ Martínez－Rodríguez J B， Montalvo I，Izquierdo J，et al.Reliability and tolerance comparison in water supply networks［J］.Water Resource Management，2011，25（5）：1437.

［5］ Rossman L A.EPANETH2 user manual［M］.Cincinnati：Environmental Protection Agency Risk Reduction Engineering Laboratory，2000.