混凝土弹塑性损伤本构模型的动力扩展

齐 虎，李云贵，吕西林

（1.同济大学 结构工程与防灾研究所，上海200092；2.中国建筑股份有限公司技术中心，北京101320）

混凝土结构都可能承受冲击、地震和爆炸等动态载荷，基于混凝土准静态力学性能的分析结果与实际情况会有较大的偏差［1］，因此，考虑应变率相关的本构模型在研究中逐渐占据重要的地位.在动力荷载作用下混凝土材料表现出应变率效应，即材料的损伤和非线性程度随应变率的增加而降低，抗拉强度和抗压强度则随应变率的增加而提高等现象［2］.混凝土材料的应变率效应在冲击荷载（如碰撞、爆炸等）以及地震荷载作用下非常明显.

研究人员很早就注意到上述现象，提出了多种动力作用下的混凝土本构模型理论，然而，由于这些理论模型本身以及数值实现算法的复杂性，工程实际中应用最为广泛的仍然是一些经验模型，如根据经验提高材料的单轴抗拉强度（或单轴抗压强度）等简化处理方法［3－4］.考虑应变加载速率的混凝土动力本构模型通常是在率不相关本构模型的基础上做如下扩展得到［5］：①将率不相关本构模型破坏面扩大［6］，在实际工程中应用较多，但没有物理背景；②将弹塑性应力—应变关系粘滞化，使得塑性应力—应变关系率相关［7］，在动力加载过程中混凝土微粒塑性应变的发展存在滞后；③考虑损伤演化的率相关性［8］，考虑了动力加载情况下混凝土材料损伤的滞后.

文献［9］通过将塑性应变和损伤变量均粘滞化，将其提出的率不相关弹塑性损伤本构模型进行动力推广，建立了相应的率相关本构模型，但模型较为复杂，使用不方便.文献［3］认为：高应变率对微裂纹发展，即损伤演化的迟滞作用导致了混凝土材料非线性程度降低及动力强度提高.文献［10］通过对损伤变量进行粘滞化，提出了适合大型钢筋混凝土结构分析的混凝土率相关弹塑性损伤本构模型，文献［2］采用和文献［10］类似的方法将提出的静力弹塑性损伤本构模型粘滞化，并通过算例表明应变率效应对实际结构的动力反应有一定的影响.

损伤力学能够从本质上描述混凝土材料内部微裂纹的开裂、发展所引起的材料宏观非线性行为，其中损伤变量的发展演化就是为了模拟材料内部微裂纹的开裂发展，从而在损伤力学中可以将损伤变量粘滞化，通过延缓损伤变量的演化来模拟高应变率对微裂纹发展的迟滞作用.笔者在以前的研究中，建议了一个混凝土率不相关弹塑性损伤本构模型［11］，该模型能较好地描述混凝土材料在静力或伪静力加载下的各种非线性行为.基于以上分析，本文将笔者建议的模型进行动力推广，使其能够描述动力加载下混凝土材料的非线性行为.

阻尼是结构振动过程中一种特有的能量耗散机制［12］.目 前 应 用 最 为 广 泛 的 是Rayleigh 阻 尼，Rayleigh阻尼假定阻尼矩阵C 是质量矩阵M 和刚度矩阵K 的线性组合，数值计算表明：单纯采用质量比例阻尼也无法减小高频噪音的影响［12］.考虑到质量比例阻尼本身并无物理依据，很多学者［9，13］都仅仅考虑刚度比例阻尼的影响.本文将刚度阻尼应力引入到建立的弹塑性损伤本构模型中，使其能在材料层次考虑阻尼的影响.利用该模型对Koyna混凝土重力坝进行了地震动作用下的非线性时程分析，分析结果与文献［9］符合较好，表明了建立模型的有效性.

本文首先简要介绍笔者建议的静力弹塑性损伤本构模型，然后对其进行扩展使之能够考虑应变率效应和刚度阻尼的影响，最后通过算例从结构位移反应和数值稳定性两个方面探讨应变率效应和刚度阻尼对结构动力反应的影响.

1 率不相关弹塑性损伤本构模型

损伤力学能描述材料的各种非线性本构行为，如刚度退化应变软化等，目前用结合塑性力学和损伤力学的弹塑性损伤本构模型来模拟混凝土材料得到了较为广泛的认同.由于塑性力学本身的复杂性，目前用大多弹塑性损伤本构模型数值处理复杂计算，效率低稳定性不好，且涉及参数较多，一般只给出了特定情况下的材料参数取值，因此较难在实际工程中应用.笔者在以前的研究中提出了一个率不相关弹塑性实用本构模型［11］，通过对弹性Helmholtz自由能进行修正，使得模型能较为准确地模拟混凝土材料在双轴、三轴加载下的非线性本构行为，其弹塑性部分使用经验弹塑性模型［10］降低模型的数值复杂性，下面首先对笔者开发的静力弹塑性损伤本构模型做简要介绍.

1.1 损伤变量的计算及参数的确定

损伤能量释放率采用如下公式计算：

式中：标记“∶”为二阶缩并积；Y±表示正、负损伤能量释放率；ψe表示修正后的弹性Helmholtz自由能；表示受拉、受压损伤变量表示有效应力张量；的正、负分量为有效柔度张量表示有效应力球量；‖X‖＝X∶X；γ 为本文引入的折减系数；δ表示向量（1，1，1，0，0，0）.

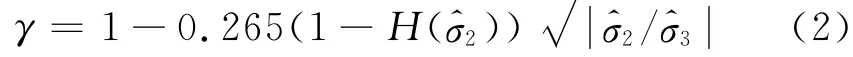
式中，H（x）为Heaviside函数.

如果式（2）计算得γ＜0，则取γ＝0.式（1）中：

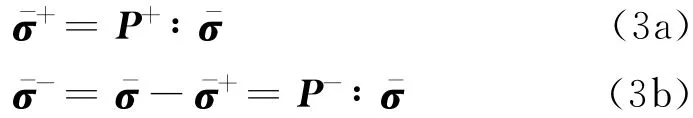
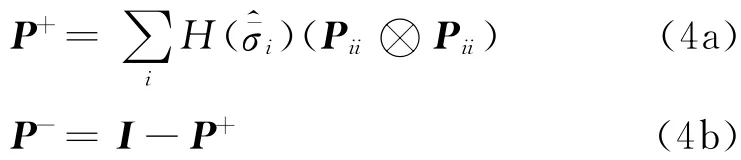
式中：标记“⊗”为张量积，Pii＝Pi⊗Pi为二阶对称张量；I为四阶一致性张量.

求出损伤能量释放率后，采用式（5）可计算出受拉、受压损伤变量d＋、d－：

加权损伤变量：

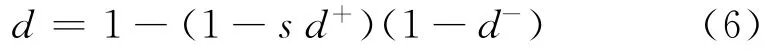
1.2 塑性应变计算

文献［10］给出如下塑性应变的经验计算公式：

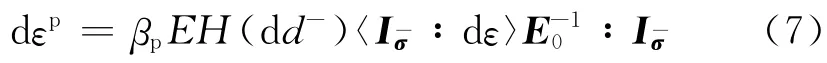
式中：εp为塑性应变，dεp表示对εp取微分；E表示材料弹性模量；E0表示材料初始弹性刚度张量为单位有效应力张量；参数βp 控制塑性应变的大小，βp∈（0，1），0 表示线弹性，1 表示理想弹塑性.本文给出如下公式计算βp 取值：

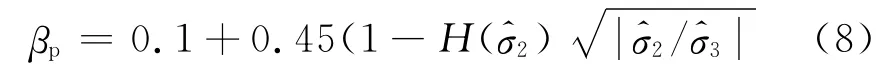
以上经验计算公式（7）—（8）大大简化了塑性应变的计算，而经典塑性理论的流动法则、塑性硬化法则等都没有得到体现.对这种非正统做法的解释是［10］：①本文模型的建立是为了分析大型实际工程，这种方法计算精度虽然不如经典塑性力学，但能大大提高计算效率并增强模型的数值稳定性；②式（7）假设弹性应变方向为塑性流动方向可视为塑性流动因子.

式（7）只考虑受压塑性应变，为了考虑受拉塑性应变，本文采用如下表达式［2］：

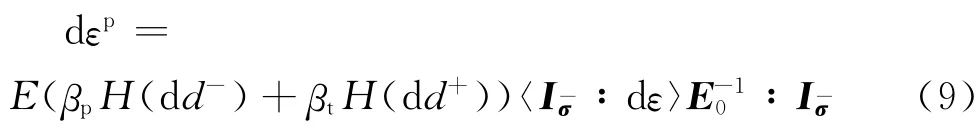
从式（9）中可以看出，参数βt 和βp 分别控制受压、受拉塑性变量发展，当受拉损伤发展即dd＋＞0时，dεp＞0，塑性应变也得到发展.

为了进一步提高模型的计算效率和稳定性，在工程实用中通常将本构曲线下降段变得缓和.这里引入受拉塑性应变在一定程度上就是为了提高模型稳定性，图1 给出了βt 对混凝土材料单轴受拉曲线的影响，可见随着βt 的增大，材料受拉骨架曲线变得更加缓和，且损伤变量的发展也变得缓慢.在从后文算例可以看出，这样处理能在一定程度上提高本构模型的稳定性.

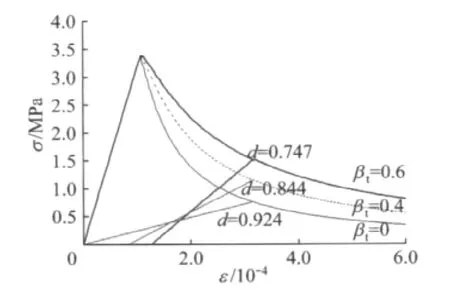
图1 单轴加载下βt 对模型受拉曲线的影响Fig.1 The influence ofβton tension curves of the model under uniaxial loading

2 损伤能量释放率Perzyna 粘滞规则化

应变率无关模型损伤能量释放率阀值直接取为损伤能量释放率的历史最大值，对于应变率相关模型，则需要对损伤能量释放率进行Perzyna粘滞规则化，文献［10］建议：

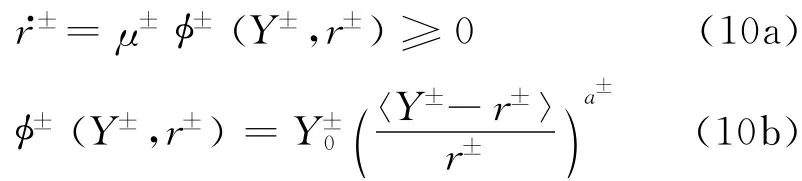
式中：r±表示拉、压损伤能量释放率阀值dt表示将r±关于时间求导；μ±为模型参数.

采用无条件稳定，且具有二次收敛精度的梯形算法［3］求解式（10），可得：

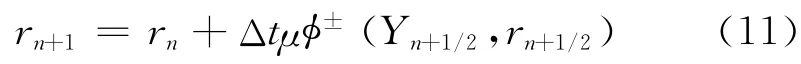
式 中：Yn＋1／2＝0.5（Yn＋Yn＋1）；rn＋1／2＝0.5（rn＋rn＋1）.

利用Newton－Raphson算法定义f（r）＝－r＋并给出迭代式：

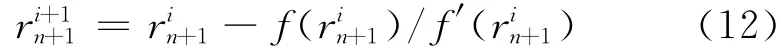
图2给出了不同应变率作用下混凝土材料的单轴受拉、单轴受压应力—应变全曲线数值模拟结果，图3给出了不同（应变率）加载条件下，混凝土材料抗拉极限承载力、抗压极限承载力数值模拟结果与相应静力强度比值（在图3 中用ρ表示）.作为对比，图3中还给出了实验结果［14］，可以看出计算结果和实验结果符合很好.材料参数为：E＝31 000MPa，泊松比ν＝0.2、单轴抗拉强度ft＝3.38 MPa、单轴抗压强度fc＝27.6 MPa.对模型其他参数，采用单轴加载进行标定，其取值分别为：μ＋＝2，μ－＝10 000，a－＝a＋＝4.

模型计算混凝土材料在应变速率分别为0.000 01、0.000 1、0.001、0.01 和0.1 时 的 单 轴 受压应力—应变滞回曲线如图4所示.

3 阻尼力的计算

为了在材料本构模型中直接考虑刚度阻尼的影响，本文在建议的弹塑性损伤本构模型中引入刚度阻尼应力.

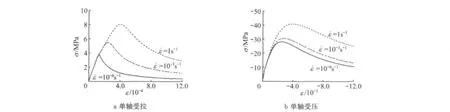
图2 单轴加载下的应变率效应Fig.2 Strain－rate effect under uniaxial loads

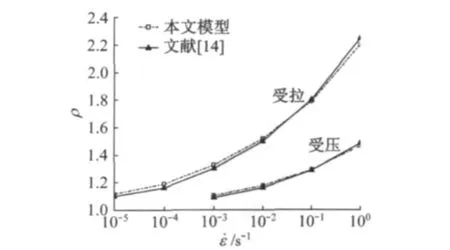
图3 模型计算结果与实验结果比较Fig.3 Comparison between calculation and experimental results

Cauchy粘滞阻尼应力σvis可表示为［9］：

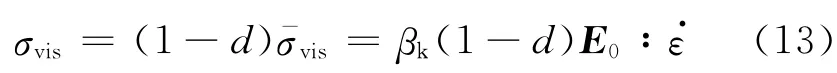
弹塑性损伤本构关系为：

式中，εe，εp分别为弹性和塑性应变.则总应力可表示如下：

图4 不同加载速率下模型应力—应变曲线Fig.4The strain stress curves of the model under different strain rates

4 一致切线模量

在有限元隐式计算中，通常采用Newton－Raphson算法求解平衡方程，此时需要用到一致切线模量，参照文献［3］，给出本文模型一致切线模量的推导过程.

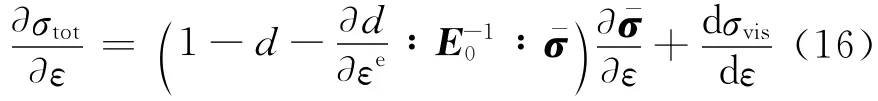
将式（7）代入式（14）并对ε求导可得：

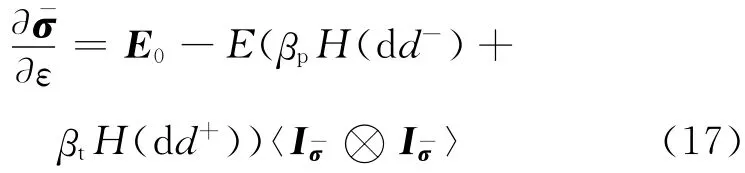
将式（6）对εe求导可得：

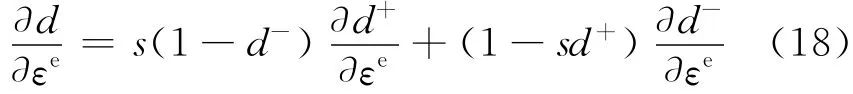
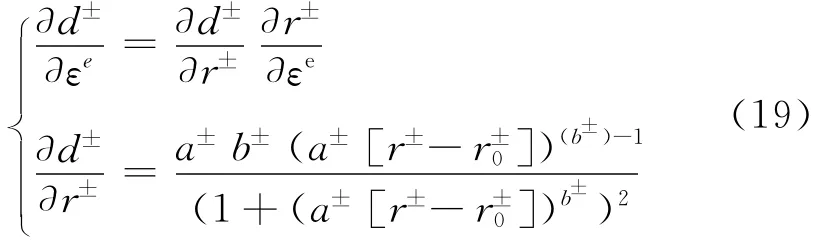
根据式（11）—（15）给出的算 法可得dr±＝λdY±［3］.其中

将式（17）—（21）代入式（16）即可求解切线刚度模量.

5 算例

应用本文建立的本构模型，对Koyna混凝土重力坝（图5）进行了数值模拟，混凝土材料参数取和文献［9］一致，分别为：密度ρ0＝2 643kg·m－3，弹性模量E＝31 027MPa，泊松比ν0＝0.2，βp＝0.5，单轴抗拉强度ft＝2.9 MPa，单轴抗压强度fc＝24.1 MPa.材料阻尼取其第一振型临界阻尼的3%.在分析中，坝体和基础之间假定为刚性连接，混凝土坝体部分网格有760个4节点平面应力单元组成，地震动引起的水对坝体的压力则通过附加质量法模拟.Koyna大坝在自重及水压力下的自振频率见表1.

图5 Koyna混凝土重力坝模型图Fig.5 Koyna concrete dam

表1 Koyna大坝在自重及水压力下的自振频率Tab.1 The nature frequency of Koyna Dam

从图6中可以看出本文模型计算位移反应和文献［9］分析结果符合较好，本文模型分析结果略大.本文在分析中发现如果不考虑刚度阻尼，分析到后期容易出现不收敛.加入刚度阻尼后，本构模型的稳定性得到显著提高，可见阻尼对结构的能量耗散作用能改善隐式动力计算的收敛性.表2给出不同情况下的计算时间，从中可知加入受拉塑性应变也能在一定程度上缩短计算时间，提高模型的稳定性，而对计算结果影响不大，本文认为这是因为考虑受拉塑性应变后材料受拉下降段变得缓和，且受拉损伤演化得到减缓从而提高模型数值稳定性.在实际分析中，混凝土的受拉性能对分析结果影响很小，但对计算收敛性的影响却很大，受拉塑性应变的引入能有效提高模型的稳定性和收敛性，从而缩短计算时间.

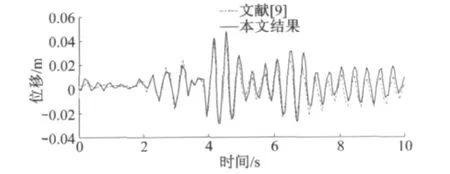
图6 率不相关模型计算坝顶相对位移时程比较Fig.6 The comparison of top dam displacements with rate independent model

表2 Koyna大坝在不同情况下所需的计算时间Tab.2 The cost time of Koyna Dam under different conditions

从图7可知，考虑应变率效应后结构顶层位移反应峰值比不考虑应变率效应略大，这点和文献［2］分析结果一致.从表2可以看出，考虑应变率效应后计算时间进一步缩短，可见考虑率应变在降低材料损伤程度的同时也提高了模型的计算效率和稳定性.

图7 应变率效应对坝顶相对位移的影响Fig.7 The effect of strain rates on dam dop displacement

图8为三种情况下（βt 均取0.5）模型损伤分布图，在不考虑刚度阻尼和应变率效应情况下加载到后期，由于模型损伤过度发展导致计算不收敛，本文在这里给出4.727s时的损伤分布图，其他两种情况均取加载结束时（10s）的损伤分布.从图8中可以看出刚度阻尼、应变率效应对材料损伤发展有显著影响，都能延缓材料损伤发展程度从而提高计算稳定性，如果在实际结构的计算分析中不考虑其影响会导致结构损伤过快发展导致计算结果失真，有时甚至会出现计算不收敛.

图8 表2所示不同情况下结构损伤分布图Fig.8 The structure damage distribution under different conditions as shown in Table 2

6 结论

本文在提出的静力弹塑性损伤本构模型的基础上，通过将损伤演化粘滞化使得模型能考虑应变加载速率的影响.在模型中引入刚度阻尼应力，使其能直接在材料层次考虑刚度阻尼耗能作用.对模型进行改进使其能考虑受拉塑性应变.将建立本构模型在ABAQUS中二次开发，通过Koyna重力坝动力隐式分析算例表明：刚度阻尼的能量耗散作用能延缓结构损伤发展程度，显著提高隐式动力计算的收敛性；混凝土受拉性能对计算稳定性有一定影响，引入受拉塑性应变后模型单轴受拉曲线下降段变得缓和，同时减缓受拉损伤变量的演化，在一定程度上增强模型的稳定性，减少计算时间；在模型中考虑应变率效应后对结构位移反应有一定的影响，同时能进一步提高模型的稳定性.

［1］ Kanehi M B，Zienkiewicz O C，Owen D R J.The visco－plastic approach to problems of plasticity and creep involving geometric nonlinear effects［J］.International Journal for Numerical Methods in Engineering，1978，12：169.

［2］ 吴建营，李杰.混凝土弹塑性损伤本构关系统一模型［J］.建筑科学与工程，2005，22（4）：15.WU Jianying，LI Jie.Unified elastoplastic damage model for concrete［J］.Journal of Architecture and Civil Engineering，2005，22（4）：15.

［3］ 吴建营，李杰.考虑应变率效应的混凝土动力弹塑性损伤本构模型［J］.同济大学学报：自然科学版，2006，34（11）：1427.WU Jianying，LI Jie.Elastoplastic damage constitutive model for concrete considering strain rate effect under dynamic loading［J］.Journal of Tongji University：Natural Science，2006，34（11）：1427.

［4］ Craig R R J.结构动力学［M］.常岭，李振邦译.北京：人民交通出版社，1996.Craig R R J.Structural dynamics［M］.Translated by CHANG Ling，LI Zhenbang.Beijing：China Communications Press，1996.

［5］ Häußler－Combe U，Kitzig M.Modeling of concrete behavior under high strain rates with inertially retarded damage［J］.International Journal of Impact Engineering，2009，36：1106.

［6］ Pandey A K，Kumar R，Paul D K，et al.Strain rate model for dynamic analysis of reinforced concrete structures［J］.Journal of Structural Engineering，2006，132（1）：393.

［7］ Barpi F.Impact behaviour of concrete：a computational approach［J］.Engineering Fracture Mechanics，2004，71（2）：197.

［8］ Suffis A，Lubrecht T A A，Combescure A.Damage model with delay effect：analytical and numerical studies of the evolution of the characteristic damage length［J］.International Journal of Solids and Structures，2003，40：346.

［9］ Lee J，Fanves G L.A plastic－damage concrete model for earthquake analysis of dams［J］.Earthquake Engineenng and Structural Dynamics，1998，27（9）：937.

［10］ Faria R，Oliver J，Cervera M.A strain－based plastic viscousdamage model for massive concrete structures ［J］.International Journal of Solids and Structures，1998，35（14）：1533.

［11］ QI Hu，LI Yungui，LÜXilin.A practical elastic plastic damage model for concrete［J］.Advanced Materials Research，2011，243－249：313.

［12］ 吴建营，李杰.反映阻尼影响的混凝土弹塑性损伤本构模型［J］.工程力学，2006，23（11）：116.WU Jianying，LI Jie.Elastoplastic damage model for concrete considering damping effects［J］.Engineering Mechanics，2006，23（11）：116.

［13］ Faria R，Vila Pouca N，Delgado R.Seismic benchmark of a R／C wall：numerical simulation and experimental validation［J］.Journal of Earthquake Engineering，2002，6（4）：473.

［14］ Suaris W，Shah S.Rate－sensitive damage theory for brittle solids［J］.ASCE，Journal of Engineering Mechanics，1984，110（6）：985.

［15］ Chopra A K，Chakrabarti P.The Koyna earthquake and the damage to Koyna dam［J］.Bulletin of the Seismological Society of America，1973，63（2）：381.