风险矩阵评估方法研究与工程应用综述

阮 欣，尹志逸，陈艾荣

（同济大学 桥梁工程系，上海200092）

近年来，风险矩阵评估方法（risk matrix method，RMM）在工程项目中的应用受到了密切关注，其概念清晰、使用方便、评估结果简洁易懂，有利于风险管理工作的开展.许多国家或地区相关部门的规范和标准中采用了风险矩阵（或其变形）评估方法，我国在隧道、桥梁、地铁等行业建议指南中，也将其作为基本的风险评估方法［1－3］.

由于不能采用试验反馈的形式对风险评估的结果进行验证，风险评估方法的可靠性和有效性一直饱受质疑［4－6］，目前的研究工作多停留在对其评估有效性的探讨之上，从方法论角度开展的研究尚不多见.

以下通过对国内外相关文献的研究，从工程应用的角度对风险矩阵评估方法进行总结，明确其数学模型、评价指标等几个基本理论问题，并探讨提高评估方法有效性的可能方向.

1 风险矩阵评估方法起源

风险（risk）一词的出现由来已久，对风险的评估和管理也可追溯至希腊、罗马时代之前，然而正式的风险分析在近代才开始出现.1922年，纽约证券交易所为计算其成员公司的资本需求量，引入了风险价值（value－at－risk）的概念.19世纪70年代，在美国环境保护局的促进下，风险评估（risk assessment）在管理中的作用得到了提升，引导了风险分析职业化.90年代期间，风险价值的概念在经济领域中得到了广泛的运用，关于风险的研究也在各个行业得到了迅速发展.

风险评估的一个重要前提是对风险内涵的深刻理解.有研究者将其概括为不确定损伤事态及其概率和后果的集合［7］，还有学者认为风险既可以是会造成损失的不确定事件本身，也可以是不确定事件发生的概率，还可以是不确定事件造成的损失期望值［8］.总体而言，研究者对风险内涵的理解基本相似：构成风险的必要因素包括风险事态（risk scenario）、风险概率（risk probability）和风险损失（risk loss）.风险矩阵评估方法RMM直接简洁地体现了对风险内涵的理解，这也是它获得广泛应用的原因之一.

风险矩阵（risk matrix）是风险矩阵评估方法的基本平台，它与投资组合理论（portfolio selection）［9］中的协方差矩阵（covariance matrix）存在显著的相似性.投资组合理论认为协方差矩阵在投资收益结算之前并不确定，而是随投资者的风险态度（risk attitude）的变化而不同［10］.风险矩阵同样不存在完全固定的形式，具体形式和内容也与决策者的风险态度息息相关.

1995年，美国空军电子系统中心在对采办项目的寿命周期风险评估工作中，首次系统地提出并广泛应用了风险矩阵评估方法［6］.

RMM方法的基本运用过程是：首先明确评估主体及需求，对其进行系统分析，给出项目风险定义；开展风险识别（risk identification），确定需评估风险事态，并采用特定方法进行风险分析（risk analysis），以描述各风险事态的概率和损失水平；最后参考决策者的风险态度，划分概率和损失等级，建立风险矩阵，并依此对各风险事态进行风险评价（risk evaluation）［11－12］.表1给出了一个典型风险矩阵［3］.

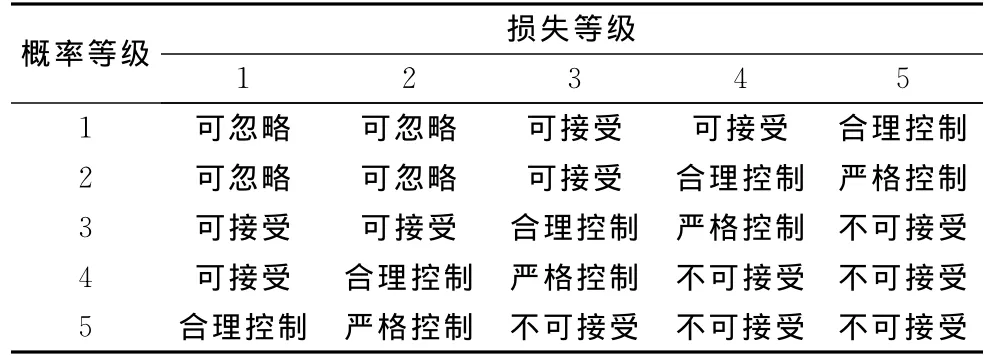
表1 典型的风险评估矩阵Tab.1 A typical risk matrix

2 风险矩阵的基本数学模型

风险矩阵的形式基本固定，可采用分级函数的形式进行描述：

式中：Rij表示风险矩阵中对应风险概率第i级和风险损失第j级的风险等级（risk ranking）；pi与lj分别表示风险概率第i级和风险损失第j级的下限；pi＋1与lj＋1分别为相对应的上限.

由表1和上述数学模型可知，风险矩阵主要包括三方面内容：矩阵阶数、表征风险等级的矩阵元素、概率和损失等级划分标准.矩阵阶数表征了评估人员对项目风险的认知程度，矩阵阶数越高，概率和损失等级的划分越细致，对评估者的认知要求越高；表征风险等级的矩阵元素与概率和损失等级划分标准则构成了具体形式，简洁地确定了风险事态的评价结果.

在不同领域的工程应用中，研究者基于不同的项目背景和决策态度，提出了不同形式的风险矩阵［13］.Cox Jr［1］对由于风险矩阵构建不当造成的错误评估结果进行了分析总结，提出了三条用于判断风险矩阵合理性的公理：弱一致性公理（weak consistency）、中间性公理（the betweenness axiom）、一致性公理（consistency coloring）.然而，这三条公理仅从逻辑兼容性（logical compatibility）的角度出发，未针对工程应用明确风险矩阵评估方法存在的实质问题，工程指导价值不显著.为深入了解风险矩阵评估方法在工程实际应用中的不足，需开展专门研究，归纳总结不当评估结果出现的原因及相应对策.

3 风险矩阵评估方法的不稳定性

由于评估者认知局限性、评估工具的不合理性等原因，工程风险评估过程中往往伴随着一定问题，导致评估结果中出现矛盾、模糊甚至错误的情况［4］，但目前没有明确的相关指标对其进行评价.为便于后续分析，不妨将这种情况定义为风险评估的不稳定性.不稳定性会造成风险管理人员对风险事态的错误认识，削弱风险评估效用.

风险识别阶段、风险分析阶段以及风险评价阶段均可能出现不稳定性问题.风险识别与分析阶段的不稳定性问题由不可避免的人为因素引起，受认知局限性的影响，这类问题广泛地存在于包含人为经验分析的过程中，无法消除；风险评价阶段的不稳定性则与风险矩阵自身形式密切相关，反映了方法固有缺陷所在，故将其定义为风险矩阵评估方法的不稳定性.

以下分别对风险矩阵评估方法各阶段出现的不稳定性做出阐述，并针对该方法的矩阵评估特点，重点分析风险评价阶段的不稳定性.

3.1 风险识别与分析阶段的不稳定性

在风险识别阶段，由于评估者认识或经验缺陷、风险文化因素差异等方面的原因［14］，可能会导致对项目风险的错误估计，造成风险事态的遗漏或不当描述，从而出现评估不稳定性.

在风险分析阶段，在风险矩阵评估方法中运用广泛的情景构建理论（scenario construction theory）对量化风险概率和损失值的讨论，以及对概率、频率和频率的概率的阐述，均说明了风险分析结果在误差影响下会出现偏差［7］，导致对风险事态概率值和损失值的有误估计，最终引起评估结果的不稳定.

3.2 风险评价阶段的不稳定性

3.2.1 风险矩阵构建过程造成的不稳定性

在现阶段工程风险矩阵评估项目中，风险矩阵的构建往往是由少数专家在参考已有“标准矩阵”的基础上，根据工程经验确定矩阵阶数、矩阵元素风险等级分配以及概率和损失等级划分边界值.在对同一风险事态进行评价的过程中，前两者造成的风险评估结果的差异显而易见，以下对后者导致的评估结果不稳定性进行具体说明.

以某桥梁工程的风险评估为例，采用如表1所示的风险矩阵，按照表2中给出的值对矩阵概率和损失等级边界进行了划分［1，13］.取某风险事态 A，其风险概率值p＝0.34，风险损失值l＝0.56，根据上述风险矩阵可知对其的评价结果为“可接受”等级.

表2 风险矩阵概率与损失等级描述Tab.2 Probability and loss ranking description in risk matrix

考虑到工程中对风险概率和损失边界估计的不确定性，并采用三角分布形式对概率及损失边界取值的不确定性进行描述，即认为风险矩阵的概率和损失等级边界值（除最小和最大边界值）在各自的±0.1区间范围内服从三角分布，且取值相互独立.

同样对风险事态A，由于风险边界值p3和l4的取值不确定，所得的评估结果将可能出现差异.当p3和l4的取值分别在［0.34，0.50］和［0.56，0.70］之间时，风险事态A的评估结果与具备确定边界的矩阵评估结果一致，为“可接受”等级；与之矛盾的评估结果包括“严格控制”等级和“合理控制”等级，出现概率分别为1.4%和23.6%，具体情况见表3.

表3 单例风险事态A风险等级划分计算表Tab.3 Risk ranking calculation for risk scenario A

造成这种不稳定性的实质原因在于：风险矩阵没有统一构建标准，构建过程无法反映决策者的真实意愿.在风险矩阵评估方法的工程应用中，受评估者认知局限性等因素影响，风险矩阵的构建存在非常大的主观性和随机性，同一工程项目中不同专家可能得到不同矩阵，导致矛盾的评估结果，造成评估不稳定性.

3.2.2 风险结的存在造成的不稳定性

工程项目的潜在风险事态多，风险矩阵评估方法在面临多风险事态的评估时，由于风险矩阵的等级划分有限，可能导致多个风险事态处于同一风险等级，出现风险结（risk tie）.风险结是指处于同一等级具有基本相同的属性还可以继续细分的风险模块.

以某地下工程项目为例，在经过风险识别和分析后，共面临8个风险事态，其概率与损失值的大小见表4.运用与3.2节相同的确定性风险矩阵进行评价，可得到各事态的风险等级（表4）.评价结果显示：8个风险事态中，有1个为“可忽略”等级，2个为“可接受”等级，2个为“合理控制”等级，3个为“严格控制”等级.由此可见，在多风险事态评估过程中，出现风险结的概率非常高.根据抽屉原理，当风险事态的数量超过风险等级数时，评价结果中必然会出现风险结.

表4 多风险事态评估结果表Tab.4 Risk assessment result for multi risk scenarios

从原理上看，风险矩阵通过对连续的风险概率值与损失值进行离散化归类，并采用风险等级形式定性描述风险水平，导致了风险结的出现.处于同一风险结中的风险事态被无差别地归为一类，无法再对其进行分类排序，造成评估结果的不稳定性.

3.2.3 风险矩阵评价形式引起的不稳定性

风险矩阵采用离散的等级形式对风险事态进行评价，对存在量级差别的极大值与较大值、极小值与较小值无法进行合理区分.

出现概率低但造成损失巨大的风险事态是工程风险评估和管理的重点.以某桥梁工程项目中风险事态J为例，其概率值与损失值分别为1.0×10－8和0.82；另有风险事态K，其概率值与损失值分别为0.78和0.17.如果采用常见的风险损失期望值表征风险值（风险值＝概率值×损失值）［1］时，事态J的风险值显然远小于事态K；当采用与3.2相同的风险矩阵进行风险评价时，事态J的评估结果为“合理控制”等级，而事态K为“可接受”等级.

造成这种差异的原因是显然的：基于风险损失期望的评估方法与风险矩阵评估方法对“风险值”的理解与表达不同.风险评估的最终目的是风险管理，其实质是一个管理过程，与评估标准密切相关，在应用过程中必须明确标准的含义.采用风险矩阵评估方法意味着接受该方法对风险的理解，比较其与风险损失期望结果之间的差异并无实质意义.

4 针对不稳定性的改进措施

风险矩阵评估方法作为一种易于执行、输出结果明确的评估方法，在工程应用中优势十分明显.相较于定量风险评估决策方法，风险矩阵评估方法凭借其模糊且有依据的判断，往往可以得出更有说服力和工程实用价值的决策方案［5］.无论是作为初步筛选风险事态的工具，还是用于实际的工程风险评估项目，风险矩阵评估方法仍具有广阔的运用前景，开展降低其评估过程中存在的不稳定性的研究很有必要.

4.1 针对风险矩阵构建过程

4.1.1 基于风险态度的风险矩阵构建

风险态度的研究对决策者的辅助作用十分有效，在经济和工程领域中均应用广泛.风险态度是指在应对显著不确定性时目标人群的选择倾向［15］.描述风险态度的理论主要包括三种，分别为投资组合理 论［9］、效 用 理 论 （utility theory）［16］和 预 期 理 论（prospect theory）［17］.

效用理论将决策者对利益和损失的态度以效用的形式进行表达，在经济和工程领域中的应用已较为普遍［16，18－19］，可作为构建风险矩阵的基本理论.基于效用理论构建风险矩阵主要包括4个步骤：利用效用函数确定决策者风险态度、求解效用无差异曲线、确定概率和损失等级划分边界值、矩阵元素风险等级分配.

4.1.2 模糊风险矩阵的构建

Markowski和Mannan［20］在风险矩阵的构建过程中 引 入 模 糊 逻 辑 （Fuzzy Logic）理 论，采 用Mamdani模糊推理算法将矩阵构建中的定性准则转换成定量结果，最后通过重心法解模糊化得出风险事态的风险值，给出其风险等级评价结果.

Markowski和 Mannan［20］针对4个风险事态，采用高斯分布对其概率和损失值进行描述后，利用传统风险矩阵（traditional risk matrix）和模糊风险矩阵（fuzzy risk matrix）分别进行了评估，模糊风险矩阵得到的评估结果较为精确，明确了各风险事态的排序.

模糊风险矩阵通过特定函数形式对风险事态的风险值进行了求解，描述了风险事态本身及风险矩阵构建过程中的不确定性，但其淡化了风险矩阵评估方法的定性特质，且避开了对决策者风险态度的讨论，无法反映出决策者在应对风险事态时的真实意愿.

4.2 针对风险结的存在

风险矩阵的固有形式决定了风险结的必然存在，由此出现的评估不稳定性不可避免.目前研究者大多致力于对矩阵方法进行改进，而不再拘泥于传统的矩阵形式.目前较为常见的方式为基于风险矩阵评估方法的基本概念，采用Borda序值法对风险事态进行风险值计算［6，21］.

Garvey和Lansdowne［21］以7个风险事态为例，分别采用传统风险矩阵和Borda序值法进行了评估，其中传统风险矩阵的评估结果中有4个风险事态处于同一个风险结中，Borda序值法的评估结果中仅有2个风险事态处于同一风险结中，具备显著的确定性优势.

Borda序值法借用了风险矩阵评估方法中风险概率和损失的概念，采用简单的排序形式对多风险事态进行了排序，并未考虑决策者的风险态度，不能在工程应用中体现决策者的要求.

4.3 针对风险矩阵评价形式

针对风险矩阵评价形式造成的不稳定性，目前开展的讨论大多停留在对不同评估方法获得的结果进行的对比上［1，6］.不同风险评估方法对风险内涵的理解各不相同，相应得到的评价结果之间显然会存在差异，由此展开的对比不仅没有意义，还可能造成对风险事态的不当认识.

5 结论与展望

风险矩阵评估RMM法概念明晰，使用简易，所得评估结果简洁易懂，便于风险管理工作的进行，在工程应用中获得了越来越多的关注，针对其评估不稳定性的研究也亟待进一步深化.通过分析风险矩阵评估方法在工程应用中存在的问题，提供了改善风险矩阵评估方法不稳定性的思路，其中针对风险评估标准与基于效用理论的风险矩阵构建过程值得深入探讨.

RMM作为风险管理的必要步骤，所得评价结果与管理决策者自身专业素质、可接受的水平以及项目资金情况等因素密切相关，在后续针对减少风险矩阵评估方法不稳定性的研究中，可对相关影响因素的标准展开深入研究探讨.

另一方面，采用效用理论对决策者风险态度进行描述，进而构建风险矩阵的方法，可有效减少因对决策者真实意愿缺乏了解而导致的不稳定性.在工程应用中可对项目决策者风险态度和效用函数的方法做出详尽研究，寻求矩阵构建的具体手段，并通过与现有矩阵的对比对其有效性做出评价.

［1］ Cox Jr L A.What’s wrong with risk matrix［J］.Risk Analysis，2008，28（2）：497.

［2］ 张喜刚.公路桥梁和隧道工程设计安全风险评估［M］.北京：人民交通出版社，2010.ZHANG Xigang.Risk assessment of highway bridge and tunnelling engineering design safety［M］.Beijing：China Communications Press，2010.

［3］ Eskesen S D，Tengborg P，Kampmann J，et al.Guidelines for tunnelling risk management： international tunnelling association，working group No.2 ［J］. Tunnelling and Underground Space Technology，2004，19：217.

［4］ Aven T，Heide B.Reliability and validity of risk analysis［J］.Reliability Engineering and System Safety，2009，94：1862.

［5］ Cox Jr L A，Babayev D，Huber W.Some limitations of qualitative risk rating systems［J］.Risk Analysis，2005，25（3）：651.

［6］ Ni H H，Chen A，Chen N.Some extensions on risk matrix approach［J］.Safety Science，2010，48：1269.

［7］ Kaplan S.The words of risk analysis［J］.Risk Analysis，1997，17（4）：407.

［8］ Hansson S O.Seven myths of risk［J］.Risk Management，2005，7（2）：7.

［9］ Markowitz H.Portfolio selection［J］.The Journal of Finance，1952，7（1）：77.

［10］ Hirschberger M，Qi Y，Steuer R E.Randomly generating portfolio－selection covariance matrices with specified distributional characteristics ［J］. European Journal of Operational Research，2005，177（2007）：1610.

［11］ Ayyub B M.Risk analysis in engineering and economics［M］.Baca Raton：Chapman ＆Hall/CRC Press，2003.

［12］ Franks A P， Maddison T.A simplified method for the estimation of individual risk ［J］. Process Safety and Environmental Protection，2006，84（B2）：101.

［13］ 阮欣，陈艾荣，石雪飞.桥梁工程风险评估［M］.北京：人民交通出版社，2008.RUAN Xin，CHEN Airong，SHI Xuefei.Risk assessment of bridge engineering［M］.Beijing：China Communications Press，2008.

［14］ Apostolakis G E.How useful is quantitative risk assessment？［J］.Risk Analysis，2004，24（3）：515.

［15］ Hillson D，Webster R M.Understanding and managing risk attitude［M］.Burlington：Gower Publishing Company，2007.

［16］ von Neumann J， Morgenstern O.Theory of games and economic behavior ［M］.3rd ed. Princeton： Princeton University Press，1953.

［17］ Kahneman D，Tversky A.Prospect theory：an analysis of decision under risk［J］.Econometrica，1979，47（2）：263.

［18］ Pratt J W，Raiffa H，Schlaifer R.Introduction to statistical decision theory［M］.Cambridge：The MIT Press，2001.

［19］ Savage L J.The foundations of statistics［M］.New York：Dover Publications Inc，1972.

［20］ Markowski A S，Mannan M S.Fuzzy risk matrix［J］.Journal of Hazardous Materials，2008，159：152.

［21］ Garvey P R，Lansdowne Z F.Risk matrix：an approach for identifying，assessing，and ranking program risks［J］.Air Journal of Logistics，1998，22（1）：18.