基于拟合与粒子群优化的VG方程参数估计

曹怀火，欧阳艾嘉，艾海男

1.池州学院 数学与计算机科学系，安徽 池州 247000

2.湖南大学 计算机与通信学院，长沙 410082

3.重庆大学 三峡库区生态环境教育部重点实验室，重庆 400045

1 引言

土壤水分特征曲线是表征土壤含水率与土壤水吸力的关系曲线，是定量研究土壤水分运动的重要参考。影响土壤水分特征曲线的因素非常复杂，通常情况下难以从理论上得出确定的关系式。因此，人们寻求一些经验公式来数值模拟土壤水分特征曲线，目前国内外最为普遍使用的描述土壤水分特征曲线的Van Genuchten方程[1]（简称VG方程）是美国学者Van Genuchten在1980年提出的，其具体表达式为：

其中θ为土壤含水率（m3/cm3）；h为土壤水吸力（cm）；θs为土壤饱和含水率（cm3/cm3）；θr为土壤残余含水率（cm3/cm3）；α,m,n为土壤水分特征曲线形状参数，m=1-1/n，n>1。

通常对于求解VG方程式（1）的参数估计问题采用间接法，即转化为如下最优化模型（2）的求解问题：

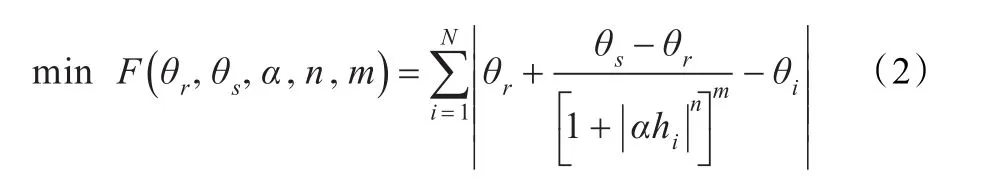
其中θi为实测土壤含水率；hi为实测土壤基质势；N为实测数据组数。传统的优化方法[2-5]大多基于梯度计算，计算效率比较高，但由于其固有的局部优化性，并不适合于全局优化问题的求解。于是很多学者对求解VG方程的参数估计问题引入了智能进化算法，如遗传算法、粒子群算法等[6-8]，同时也取得了一定的效果。

由于遗传算法和粒子群算法受初值影响，易于产生局部最优解等缺陷，目前很多学者给出了一些改进的遗传算法[9]和改进的粒子群算法[10]。为了提高粒子群算法的收敛概率和减少迭代次数，综合文献[11-12]方法的思想，将lsqcurvefit拟合方法与粒子群优化算法相结合，构造一种新的混合型粒子群优化算法，并用于求解VG方程的参数估计问题。该算法不仅包含粒子群算法的全局搜索能力，还具有lsqcurvefit拟合函数较强的局部优化能力。

2 算法构造

2.1 粒子群优化（PSO）算法简介

粒子群优化算法是一种进化计算技术，它是模仿鸟群或鱼群的社会行为而提出的算法。首先初始化一群随机粒子，然后粒子们就追随当前的最优粒子在解空间中搜索，即通过迭代找到最优解。假设d维搜索空间中的第i个粒子的位置和速度分别为Xi=(xi1,xi2,…,xid)和Vi=(vi1,vi2,…,vid)，在每一次迭代中，粒子通过跟踪两个最优解来更新自己，第一个就是粒子本身所找到的最优解，即个体极值pbest，Pi=(pi1,pi2,…,pid)；另一个是整个种群目前找到的最优解，即全局最优解gbest，在找到这两个最优解时，粒子根据如下公式来更新自己的速度和新的位置：

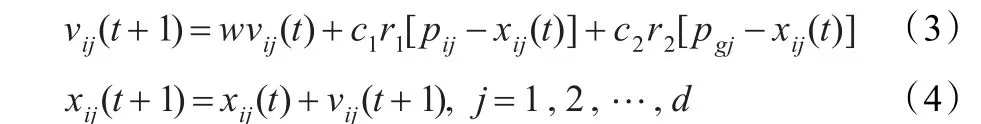
其中w为惯性权因子，c1和c2为正的学习因子，r1和r2为0到1之间均匀分布的随机数。

2.2 基于Lsqcurvefit拟合的粒子群优化算法

PSO算法的搜优速度在一定程度上快于其他进化算法，但却存在全局搜索能力极强而局部寻优能力比较差，也就是说该算法可以用于极快的速度搜索到最优解附近，但要进一步达到最优解则速度很慢。为了加快局部寻优能力，将lsqcurvefit拟合方法与PSO算法相结合，构造一种新的混合型粒子群优化算法（LPSO算法），其基本思路是在进化过程当中利用非线性拟合函数lsqcurvefit优化初始种群，通过lsqcurvefit函数较强的局部优化能力来提高收敛速度，进而同时具有PSO算法的全局优化能力和lsqcurvefit拟合方法的高效局部优化能力。主要步骤如下：

步骤1随机初始化种群中各微粒的位置和速度，并确定粒子种群规模N、学习因子c1，c2以及惯性权因子w。

步骤2用Matlab中的非线性拟合函数lsqcurvefit优化初始种群位置，其调用格式为：

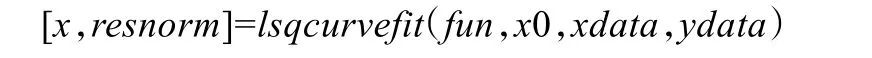
其中X为优化后的初始种群，resnorm为要返回的残差平方和，fun为拟合函数，x0为初始种群，xdata、ydata分别为实测数据。

步骤3计算每个微粒的适应值，并将当前各微粒的位置和适应值存储在各微粒的pbest中，将所有pbest中适应值最优个体的位置和适应值存储于gbest中。

步骤4用式（3）～（4）更新各微粒的速度和位移。

步骤5对于每个微粒，将其适应值与其经历过的最好位置作比较，如果较好，则将其作为当前的最好位置。

步骤6比较当前所有pbest和gbest的值，更新gbest。

步骤7若满足停止条件，搜索停止，输出结果，否则返回步骤4继续搜索。

3 数值实验与结果分析

3.1 数值实验

为了验证所提出的LPSO算法的优化性能和优化精度，以石家庄农业现代化研究所栾城实验站提供的土壤数据[3]为例。算法的参数设置为：学习因子c1=c2=1.2，粒子数N=200，惯性权因子w=0.45，最大迭代次数为1 000次。在计算过程当中，参数α，n，θs，θr的取值范围为[0，5]。

验证分成两部分。第一部分是分别采用LPSO算法与PSO算法进行求解VG方程参数的40次数值实验，以分析其能够收敛的次数、收敛效率以及收敛迭代次数来比较两者的优缺点。第二部分从最优化准则函数值的角度，分别采用lsqcurvefit拟合方法、PSO算法和LPSO算法对VG方程的参数进行估计，以比较LPSO算法与PSO算法以及lsqcurvefit拟合函数的最优值。

3.2 结果分析

表1给出了LPSO算法与PSO算法的优化性能结果比较。由表1可以看出，LPSO算法的收敛次数为40次，收敛概率为100%，而PSO算法的收敛次数仅有7次，收敛概率为17.5%。由此可见，在收敛性能上，由于LPSO算法引入lsqcurvefit拟合函数，使其收敛效率比PSO算法大大提高。从收敛时迭代次数的分布来看，LPSO算法的收敛迭代次数在区间[101，200]的次数最大达到22次，而PSO算法在区间[101，200]的收敛迭代次数仅有3次。因此，LPSO算法与PSO算法相比，不但收敛效率提高，而且收敛迭代次数也大大增加。

表2给出了lsqcurvefit拟合方法、PSO算法和LPSO算法估计VG方程参数的函数最优值结果比较。由表2可以看出，LPSO算法的结果要比lsqcurvefit拟合[3]方法、PSO算法的结果都小一些。另外，lsqcurvefit拟合方法对参数初值的依赖很强，而LPSO算法没必要给出各参数的初值。综合可见，LPSO算法对参数估计的结果要优于lsqcurvefit拟合方法和PSO算法计算的结果。

表1 VG方程的粒子群算法优化性能比较

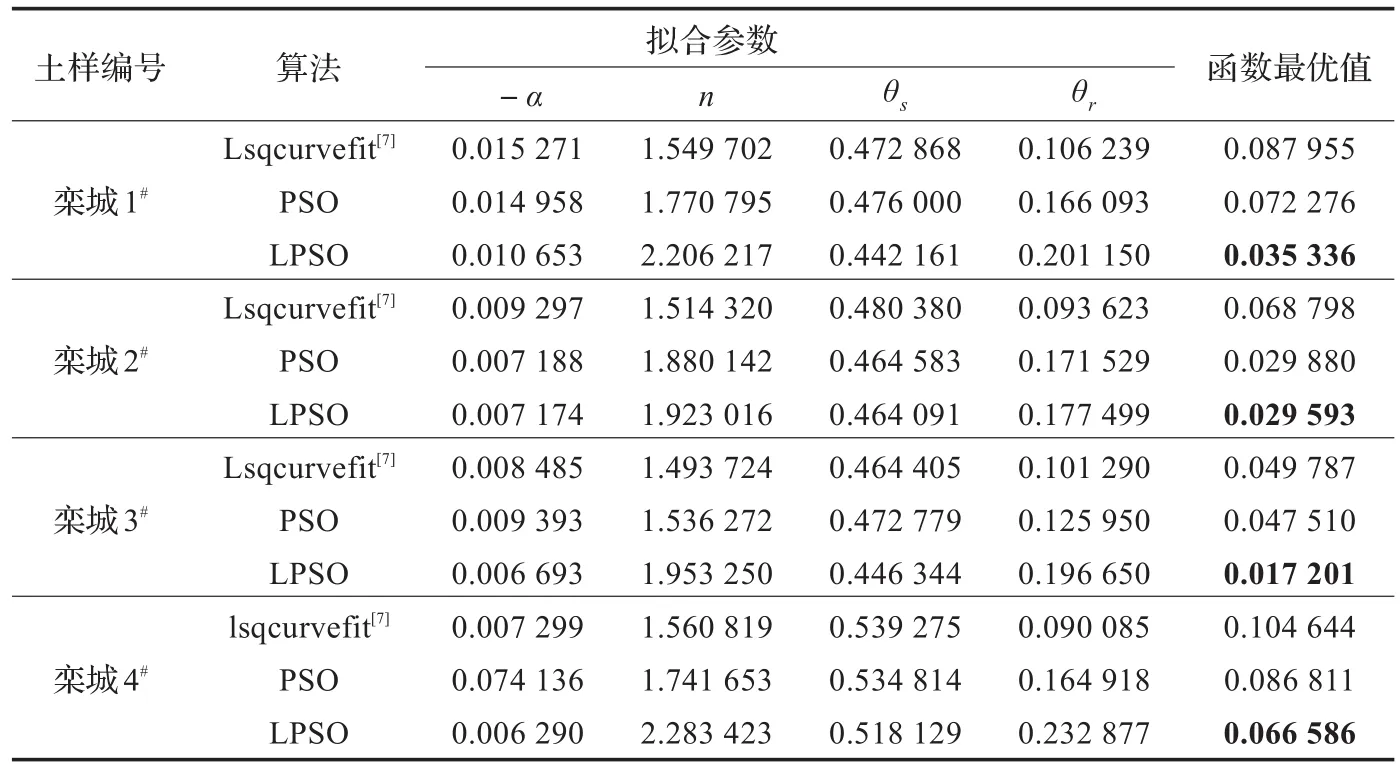
表2 VG方程的参数估计结果比较

4 结束语

本文将lsqcurvefit拟合方法与粒子群（PSO）算法相结合，实现了不同土样的土壤水分特征曲线VG方程的参数估计，并与PSO算法和lsqcurvefit拟合方法相比较，结果表明了LPSO算法求解VG方程参数效果更好，避免了初值选取和陷入局部最优解的问题。另外该算法也可适用于其他类似的非线性参数估计问题。

[1]Van Genuchten M.A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J].Soil Sci Soc Am J，1980，44：892-898.

[2]马英杰，虎胆·吐马尔拜，沈冰.利用阻尼最小二乘法求解Van Genuchten方程参数[J].农业工程学报，2005，21（8）：l79-180.

[3]彭建平，邵爱军.用MATLAB确定土壤水分特征曲线参数[J].土壤，2007，39（3）：433-438.

[4]杨改强，霍丽娟，杨国义，等.利用MATLAB拟合van Genuchten方程参数的研究[J].土壤，2010，42（2）：268-274.

[5]王小华，贾克力，刘景辉，等.Van Genuchten模型在土壤水分特征曲线拟合分析中的应用[J].干旱地区农业研究，2009，27（2）：179-183.

[6]许小健，黄小平，张金轮.用遗传算法优化估计Van Genuchten方程参数[J].岩土工程技术，2008，22（2）：75-78.

[7]郭向红，孙西欢，马娟娟.基于混合遗传算法估计Van Genuchten方程参数[J].水科学进展，2009，20（5）：677-682.

[8]陈大春，马英杰.基于随机粒子群算法的Van Genuchten方程参数优化求解[J].农业工程学报，2006，22（12）：82-84.

[9]谭跃，谭冠政，叶勇，等.具有混沌局部搜索策略的双种群遗传算法[J].计算机应用研究，2011，28（2）：469-471.

[10]张艳琼.改进的云自适应粒子群优化算法[J].计算机应用研究，2010，27（9）：3250-3252.

[11]艾海男，刘利斌，张永，等.基于Lingo和单纯形算法的综合暴雨强度公式参数解析[J].中国给水排水，2011，27（17）：71-74.

[12]刘利斌，欧阳艾嘉，乐光学，等.基于混合粒子群的土壤水分特征曲线参数优化[J].计算机工程与应用，2011，47（35）：218-221.