浅谈二维晶胞的选取

陈世明

（扬中市新坝中学江苏扬中212200）

浅谈二维晶胞的选取

陈世明

（扬中市新坝中学江苏扬中212200）

晶体是高中化学竞赛的必考内容，其中晶胞的选择是一个难点。本文结合具体的实例讨论晶体二维结构中二维晶胞的选取方法。

一、结构基元的选取和点阵点

晶体是具有规则几何外形的固体。晶体宏观结构上的规则几何外形是晶体内部粒子（原子、分子或离子）在空间按规律周期性排列的反映。研究晶体微观结构可以将其分解为两个要素：一个是周期性重复的内容，即结构基元；另一个就是重复周期的大小与方向，通常用点阵来表示。可简单地将晶体结构示意表示为：晶体结构=点阵+结构基元。

将晶体结构中每一个结构基元抽象为一个点，称为点阵点。点阵则是由无限个点阵点构成。点阵的一个基本特点是：连接其中任意两点可得一向量，将各个点按此向量平移，能使它复原，即平移对称性。

例1：下图1是石墨晶体的一层（每个黑色实心球表示一个碳原子），请找出其中的平面点阵。

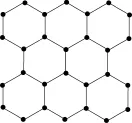
图1 石墨的层状结构

解析：从上图我们很容易看出，石墨平面结构是由很多个等同的平面正六边形构成的。

1个正六边形中平均占有2个碳原子（每个六边形有6个顶点碳原子，每个顶点只占1/ 3，所以每个正六边形占有6× 1/3=2个碳原子）。于是用一个点阵点表示这2个碳原子。这个点的位置是可以任意选取的，所以，可以有多种表示点阵的方法。如下图（空心球表示点阵点）：

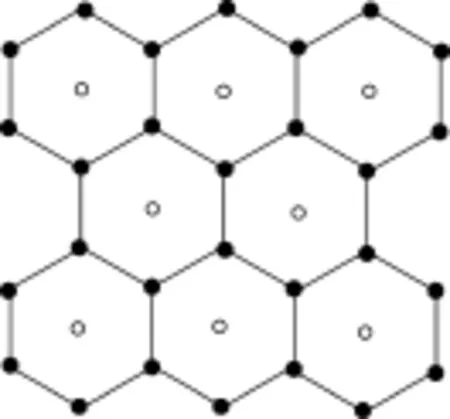
图2 将点阵点放在每个六边形的面心

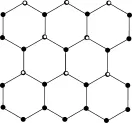
图3 将点阵点放在每个六边形的最上方的顶点

在石墨的平面结构中为什么不能将每个C原子看作结构基元，再抽象成点阵点？如果这样做，则不满足点阵的平移对称性：如下图4，将点阵点放在每个碳原子的位置，连接最近的两个点阵点得到一个向量，将此点阵中所有点沿此向量平移，在“？”处没有点阵点，不能复原。

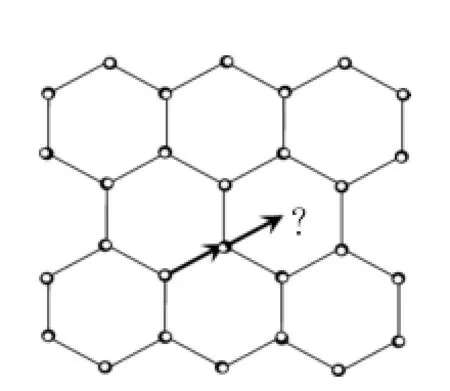
图4 石墨层状结构点阵点的错误选取

二、二维晶胞的选取

在晶体微观平面结构中，按照晶体内部结构的周期性，划分出一个个大小和形状完全一样的平行四边形，以代表晶体结构的基本重复单位，叫平面晶胞（或二维晶胞）。

例2：（2003全国初赛，第六题第2问）2003年3月日本筑波材料科学国家实验室一个研究小组发现首例带结晶水的晶体在5K下呈现超导性。据报道，该晶体的化学式为Na0.35CoO2·1.3H2O，具有……-CoO2-H2O-Na-H2O-CoO2-H2O-Na-H2O-……层状结构；在以“CoO2”为最简式表示的二维结构中，钴原子和氧原子呈周期性排列，钴原子被4个氧原子包围，Co-O键等长。

图5

解析：首先分析一下石墨的二维晶胞是如何选取的：如上述图2，取每个正六边形的面心为点阵点，连接两个最短的不共线的向量得到一个六方格子。六方格子放入二维晶体中就得到二维晶胞。当然通过平移此六方格子可以得到二维晶胞的其他选择方式（如下图6，7）。

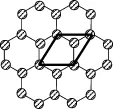
图6

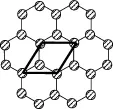
图7

再来分析CoO2层的结构中二维晶胞的选取。

第1步：画出CoO2层的结构。根据钴原子被4个氧原子包围，Co-O键等长。可以得出Co原子和O原子的位置的基本关系（如图8，假设为正方形）。将这些结构无间隙地排列，得图9，此结构中Co和O原子个数比为1∶1，不满足题意。应该有规律地去掉一半Co原子，得图10，即为CoO2层的结构。

图8

图9

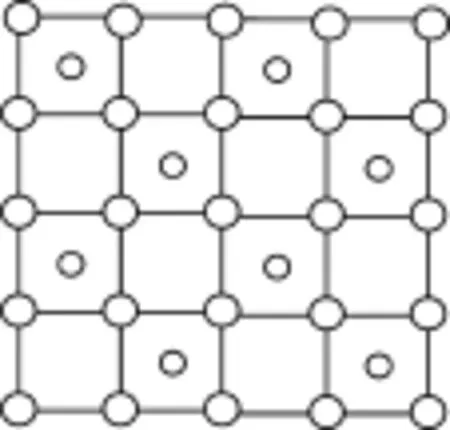
图10

第2步：找出结构基元并用点阵点表示。可以发现此结构的结构基元为图13虚椭圆框所示的部分，将此抽象为点阵点（图11，12中黑心实球表示点阵点），并放在左方的一个氧原子上，得到点阵。

图11

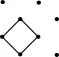
图12

第3步：平面格子的选取。如图12，此点阵单位为正方形格子。

第4步：将上述所取的正方形格子放入CoO2层的结构中，可以得到CoO2的二维晶胞。正方形格子放的位置不同可得到不同的晶胞。如下图13-17等。

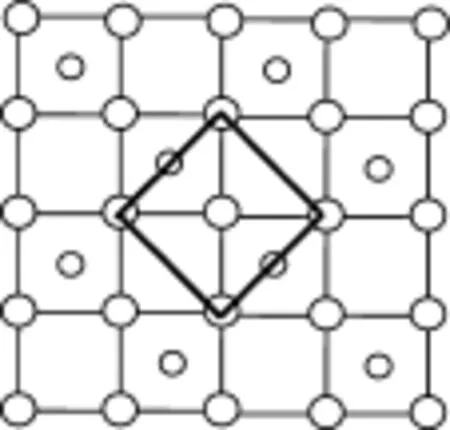
图13

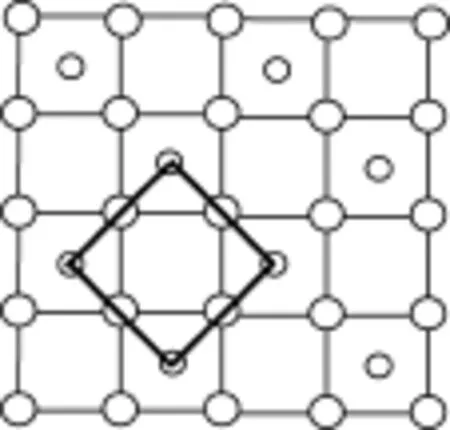
图14

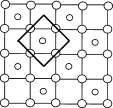
图15

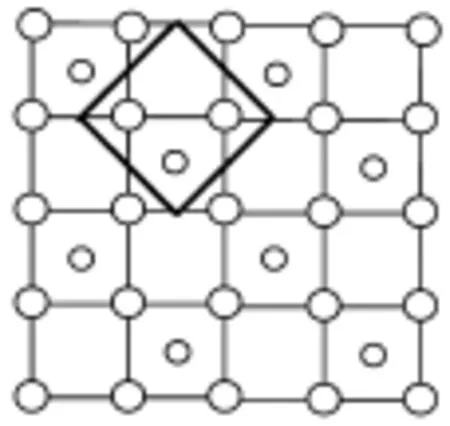
图16

图17

刚才假设图8为正方形，如果图8为长方形呢（如下图18）？根据上述步骤，最后得到矩形带心的晶胞。如下图19-22等。

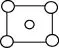
图18

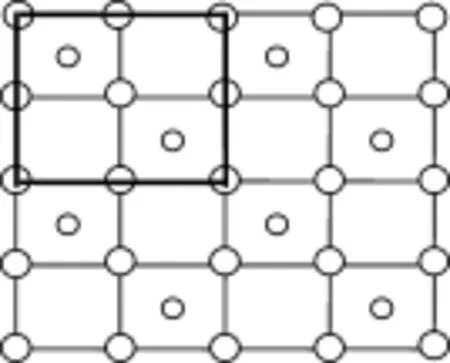
图19

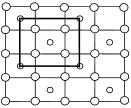
图20

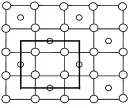
图21

图22

综上所述，晶体二维结构中二维晶胞的选取方法可以通过选平面格子的方法经过3步完成：一、选取结构基元，确定点阵，点阵点的位置可由多种选法；二、准确找出平面格子，正当的平面格子只有一种；三、将平面格子放入晶体二维结构中，平面格子及其所包含的粒子即为二维晶胞。平面格子所放的位置不是唯一的，所以晶胞可有多种选取方式。

［1］周公度，段连运.结构化学基础［M］.北京：北京大学出版社，2008

［2］北京师范大学等校.无机化学（上册）［M］.北京：高等教育出版社，2002

［3］马宏佳.高中化学奥赛试题评析［M］.南京：南京师范大学出版社，2005

1008-0546（2013）08-0089-02

G633.8

B

10.3969/j.issn.1008-0546.2013.08.034