基于交叉验证LSSVM的大坝监测数据处理模型

徐 南,陈逸凡,吴 彦

(1.河海大学地球科学与工程学院,江苏南京210098;2.河海大学水利水电学院,江苏南京210098)

0 引 言

目前大坝安全监测主要采用统计模型、确定模型、混合模型对监测数据进行处理和分析。这些数学模型都包含一定的统计特性,或建立在观测误差期望为零、各次观测相互独立及观测误差服从正态分布的前提条件下,或建立在对大坝物理力学性质的一定假设基础上,故模型精度取决于建模因子的选取是否合理。此外,时效因素的分析较为复杂,存在一定不确定性。因此,利用上述模型对监测数据进行拟合的精度一般不是很高。

最小二乘支持向量机(LSSVM)是基于统计学习理论发展起来的一种新的机器学习技术,它以坚实的理论基础、较强的学习能力和泛化能力,正在成为继神经网络之后机器学习领域新的研究热点[1]。支持向量机能够很好解决高维数、小样本和非线性等难题,成功应用于分类、逼近和预测等问题;大坝监测数据具有非线性、复杂性等特点,故可以使用支持向量机构建大坝监测数据处理模型[2];但是普通LSSVM模型存在惩罚参数c和核函数参数g由于任意给定或者凭测试经验给定的问题,因此本文使用交叉验证法搜索最优模型参数,以建立更为科学合理的大坝监测数据处理模型[3]。

1 大坝变形监测的LSSVM模型

1.1 LSSVM模型

最小二乘支持向量机(LSSVM)的基本思想是通过非线性映射,将输入数据投影到高维特征空间,并在这个高维空间进行线性回归[4]。具体原理如下:给定m个样本集合{xi,yi},i=1,2,…,m;xi∈Rn输入;yi∈R是输出。最优决策函数:

且上式应该满足如下条件:

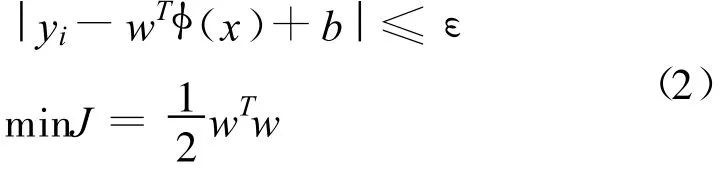
定义误差损失函数为误差的二次项,则上述问题可以转化为

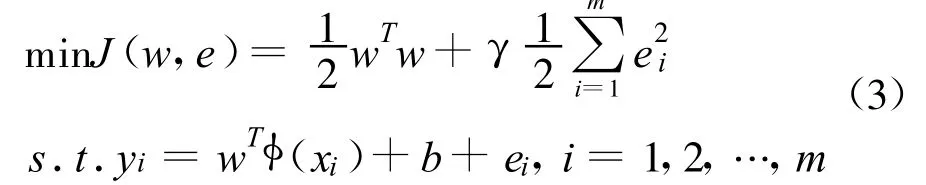
式(3)中,γ为惩罚系数,用来控制对超出误差e的样本的惩罚程度。引进Lagrange函数:

定义核函数K(xi,xj)=φ(xi)Tφ(xj),最终的预测模型可表达为:

径向基函数是较为通用的核函数,本文选取径向基核函数作为模型核函数:

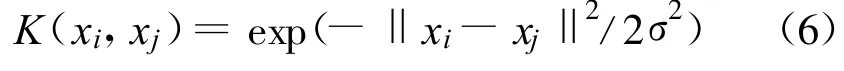
其中,σ是核函数参数,是一个预先设定好的常数,简称核系数。

1.2 交叉验证法优化LSSVM模型

传统LSSVM模型中惩罚参数c和核函数参数g是任意给定或者凭测试经验给定的,存在很大的主观性和随意性,本文针对此缺陷采用交叉验证法搜索最优参数,优化LSSVM模型。

交叉验证法的基本思想是首先对原始数据进行分类,一部分作为训练集,另一部分作为验证集,首先用训练集对模型进行训练,再利用验证集测试训练得到的模型,以此作为评价模型的性能指标。当模型性能指标取得最大值时,此时可以求出最佳模型参数c和g。

基于交叉验证LSSVM模型算法流程如下:

(1)根据模型假设选定因变量和自变量;

(2)对原始数据进行预处理;

(3)使用交叉验证法搜索最优模型回归参数 c和g;

(4)利用交叉验证法搜索最优回归参数c和g,并构建LSSVM模型;

(5)对模型进行测试,评价模型测试效果。

2 实例分析

为分析本文提出的模型以及验证该模型在大坝观测数据处理中的优越性,现利用文献[5]中的数据对该模型进行测试,具体数据如表1所示。

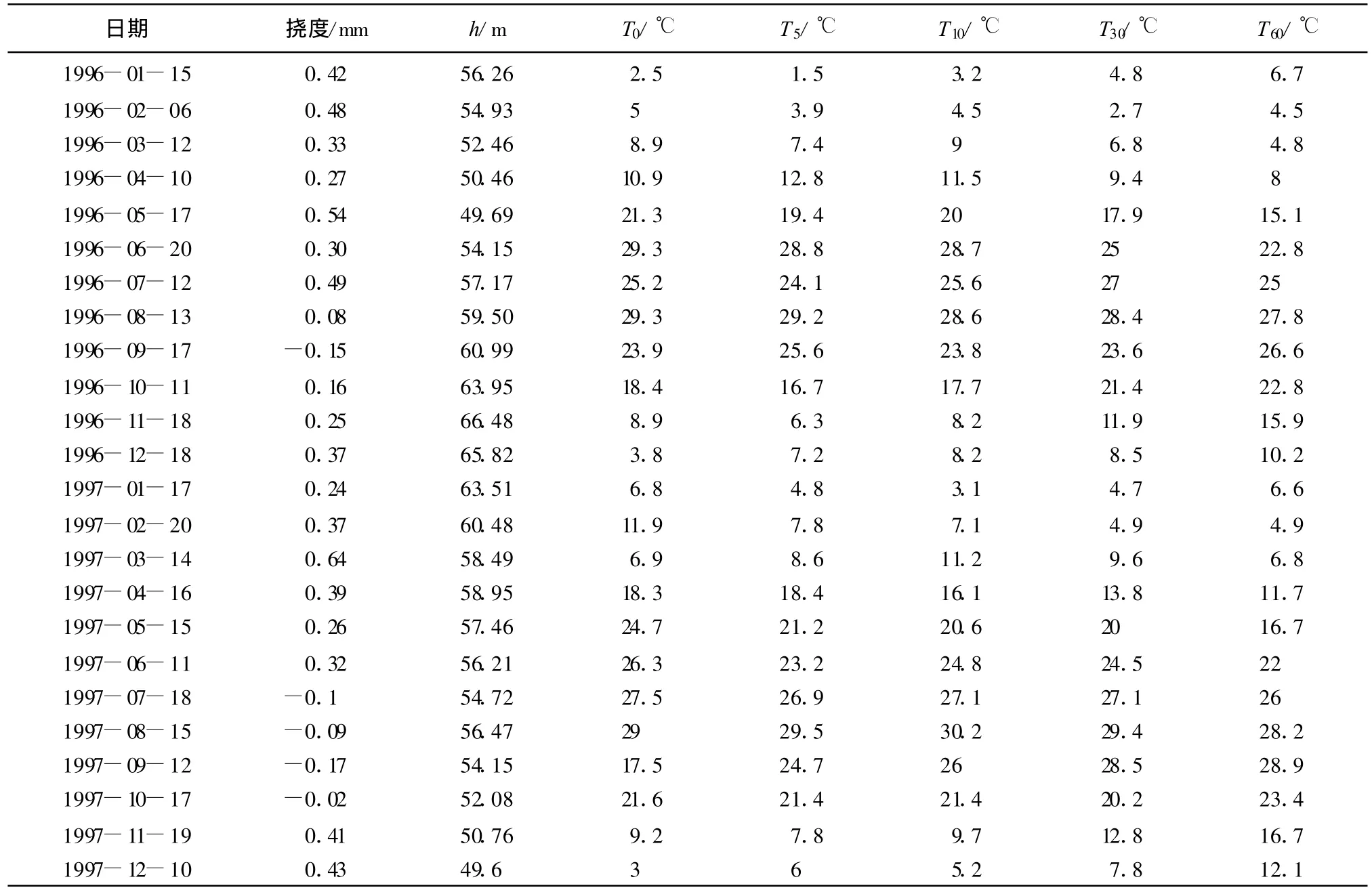
表1 丹江口大坝某坝段1996、1997年观测数据

将观测数据分为两个部分,以1996-07-12和1996-12-18、1997-06-11和 1997-12-10的数据作为测试数据,其余作为模型训练数据。利用训练数据构建LSSVM模型,输入向量有大坝上下游水位差因子 h,温度因子 T0、T5、T10、T30、T60(分别为当天、前5天、前10天、前30天、前 60天当地平均气温)共6个因子组成,输出为大坝挠度值。在此基础上,使用所构建的LSSVM模型,利用交叉验证法进行全局最优搜索,搜索结果即最优模型参数为:c=4,g=0.0625;利用最终的最优模型参数构建LSSVM模型,对待测试数据进行测试。

表2 测试数据实测值和预测值相对误差对比

将本文模型测试得到的结果和文献[5]中的结果相比较,如表2所示:文献[5]中模型最大相对误差为10.8%,本文模型最大相对误差为0.7403%;文献[5]中模型中误差为0.033本文模型中误差为0.0020 m。

由表2得出,本文提出的模型对测试数据的拟合效果明显优于文献[5]中的拟合效果;结合表2中测试数据实测值和预测值相对误差对比,可以发现本文所构建的基于交叉验证法LSSVM模型具有明显的优越性,能够快速地搜索最优模型参数,使得模型具有很好的预测效果,因此可以用于大坝监测数据处理中。

3 结 论

本文利用交叉验证法搜索最优LSSVM模型参数,解决了模型中惩罚参数c和核函数参数g由于任意给定或者凭测试经验给定而带来的问题,使得模型精度更高、鲁棒性更强。通过计算得到,文献[5]中模型中误差为0.0332 m,本文模型中误差为0.0020 m,故本文模型比文献[5]中模型有明显的优越性。综上,本文将交叉验证的LSSVM模型引入大坝观测数据处理中,通过实例计算论证了该模型在大坝观测数据处理中有较高的实用价值。

[1] 曾 杰,张 华.基于最小二乘支持向量机的风速预测模型[J].电网技术,2009,(18):144-147.

[2] 高永刚,岳建平.石杏喜支持向量机在变形监测数据处理中的应用[J].水电自动化与大坝监测,2005,29(5):36-39.

[3] 王 凯,侯著荣,王聪丽.基于交叉验证SVM的网络入侵检测[J].测试技术学报,2010,24(5):419-423.

[4] 白 鹏,张喜斌,张 斌,等.支持向量机理论及工程应用实例[M].西安:西安电子科技大学出版社,2008:14-15.

[5] 徐 晖,李 钢.基于MATLAB的BP神经网络在大坝观测数据处理中的应用[J].武汉大学学报,2005,38(3):50-53.