坝体宽高比对面板堆石坝变形特性的影响分析
李 博
(中工武大设计研究有限公司,湖北武汉430072)
0 前 言
一般来说,由于拱效应的存在,河谷形状对面板堆石坝坝体变形模量有较为显著的影响。宽阔型河谷,大坝变形模量较低,坝体变形大;狭窄型河谷,大坝变形模量较高,坝体变形相对较小。常用表征河谷宽窄的指标主要有宽高比和巴西COPEL公司提出的谷形系数[1](A/H2,A为面板面积),两种指标大体相当,其值越大,河谷越宽阔。
为研究河谷形状对面板堆石坝变形特性影响,宋文晶等[2]通过多个实际工程案例,分析了河谷地形对混凝土面板运行状态的影响,认为坝基面开挖形状的突变引起堆石体的不均匀变形往往会导致面板的应力集中及接缝系统的破坏。周伟等[3]的研究认为当河谷形状系数(A/H2)大于4.0后,河谷拱效应对大坝变形的影响很小,而狭窄河谷产生的拱效应会在一定程度上抑制堆石体初期的变形速率,随着堆石体蠕变的发展,堆石体的拱效应也随之逐渐减弱。朱晟等[4]对某200 m级狭窄河谷面板堆石坝进行应力变形数值分析,认为狭窄的河谷使得坝体沉降极值位置上抬,复杂的河谷地形也让该坝呈现出与一般面板堆石坝明显不同的变形分布规律。程嵩[5]等的研究认为,宽高比减小会导致坝体变形、面板挠度以及周边缝开度减小,增大顺坡向应力。目前关于河谷形状对坝体应力变形影响的研究还不多,一些已建工程也表明,狭窄河谷或复杂的河谷形状可能会导致坝体出现裂缝,影响大坝安全[2],因此有必要研究河谷形状对面板堆石坝变形性状的影响。本文基于三维有限元数值分析,通过对不同河谷宽度条件下面板堆石坝变形特性的对比分析,重点研究宽高比这一指标对大坝变形特征的影响规律,以期为面板堆石坝的设计提供一定借鉴。
1 计算方法与计算条件
一些研究表明,邓肯EB模型[6]能够较好地模拟堆石体的非线性应力变形关系,且具有概念明确、方法成熟等优点,在土石坝应力变形数值分析中应用最为广泛[7]。本文采用邓肯EB模型模拟堆石料的应力变形行为。
本文采用非线性增量计算方法,计算过程中按照坝体施工和蓄水的先后顺序先模拟堆石体逐步填筑过程,后模拟逐步蓄水过程。
根据本文的研究目的,以坝高为150 m的理想面板堆石坝为研究对象,坝顶宽10 m,上下游坝坡坡比均为1∶1.4,河谷采用U型对称河谷,两岸边坡平均坡度为1∶0.83。计算分析采用了4种不同的宽高比方案,分别为1.8、2.0、3.0和4.0。为使对比研究更具针对性,在4种比较方案中,保持两岸坡度一致,仅通过调整河床宽度来改变大坝的宽高比,有限元计算模型如图1所示。
静力计算中主要考虑了坝体自重、静水压力等荷载,上游水位高程 140 m(假定建基面高程为0 m),下游无水。
2 宽高比对面板堆石坝变形特性影响
2.1 宽高比对坝体沉降的影响
图2给出了坝体最大断面坝轴线沉降沿高程的分布图,由图可知,不同宽高比情况下,沉降的分布规律基本一致,无论是填筑完成时还是满蓄时,坝体沉降最大值均发生在约1/2坝高(约72 m高程)处,即使在宽高比仅1.8的狭窄河谷中,坝体沉降的分布规律与一般面板堆石坝亦无明显区别,因此本例中宽高比对坝体沉降分布规律影响不大。与文献[4]沉降极值位置上抬的结论不同的是,本文例子中的河谷形状呈U型,且边坡自上而下逐渐变缓,文献[4]中的河谷形状呈V型,且河谷边坡在1/2坝高以上较为宽缓,在1/2坝高以下迅速收窄,形成非常明显的顶托作用,造成了坝体沉降极值出现上抬现象。
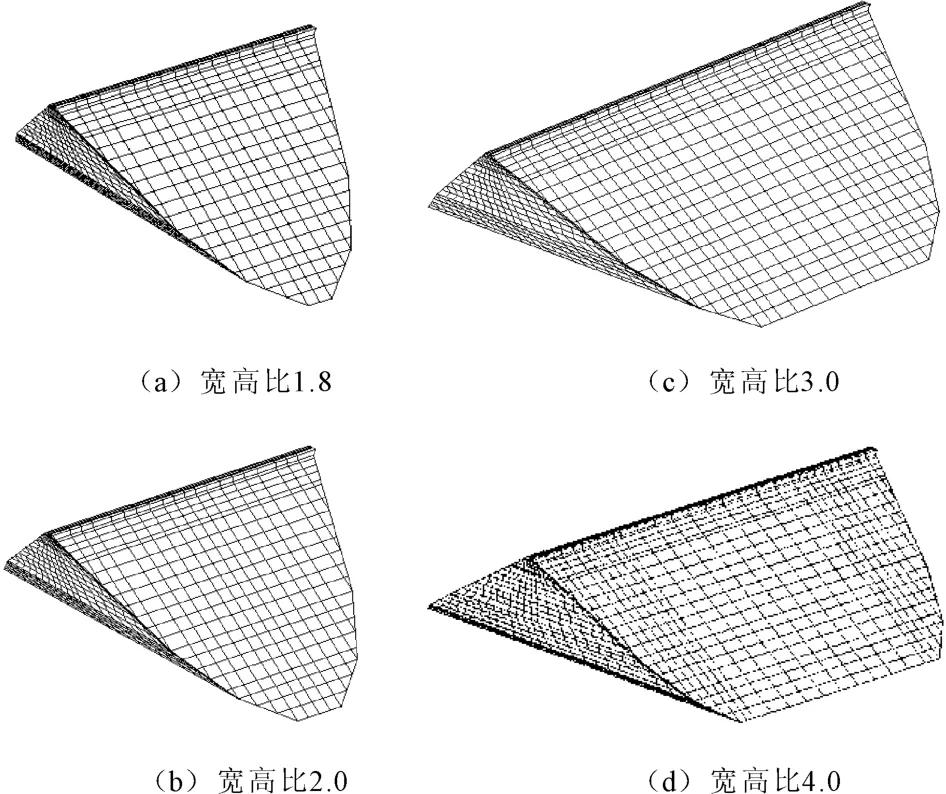
图1 有限元计算分析模型

图2 坝体最大断面坝轴线沉降分布图
图3为宽高比与坝体沉降极值的关系曲线,在宽高比小于3.0时,宽高比对沉降极值的影响较为明显,并随着宽高比的增大,影响逐渐减小。对于竣工期,宽高比由1.8增大至2.0时,沉降极值增加了8.6 cm,宽高比由2.0增大至3.0时,沉降极值增加了11.7 cm。当宽高比大于3.0时,河谷宽度对大坝沉降分布影响非常小,不论是竣工期还是蓄水期,宽高比为3.0和4.0的沉降分布和极值几乎一致。
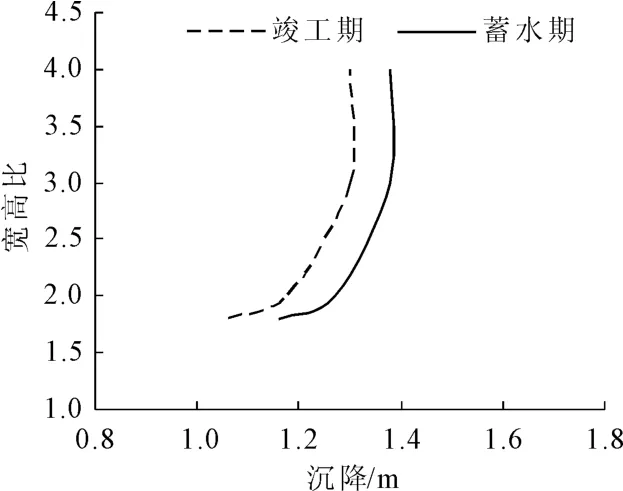
图3 宽高比与最大沉降的关系曲线
蓄水引起的沉降在0.06 m~0.09 m之间,随宽高比增大而减小,蓄水引起的沉降受宽高比影响较小。
与坝体沉降分布相对应的是坝体竖直向应力分布(见图4),在1/2坝高以上,不论是宽河谷还是窄河谷,坝体竖直向应力基本与土柱应力分布近似,说明河谷形状对应力分布影响很小,拱效应不明显。自1/2坝高向下,由于河谷逐渐变窄,宽高比为1.8和2.0两种方案下竖直向应力随高程降低的增加速率有明显地降低,宽高比1.8的底部还出现了应力降低,就竣工期而言,宽高比1.8的坝底部竖向应力为1.9MPa,而宽高比2.0则增加到2.3MPa,河谷拱效应较为明显。宽高比为3.0和4.0两种方案下,竖直向应力曲线斜率与1/2坝高以上较为接近,坝底部应力也基本一致。
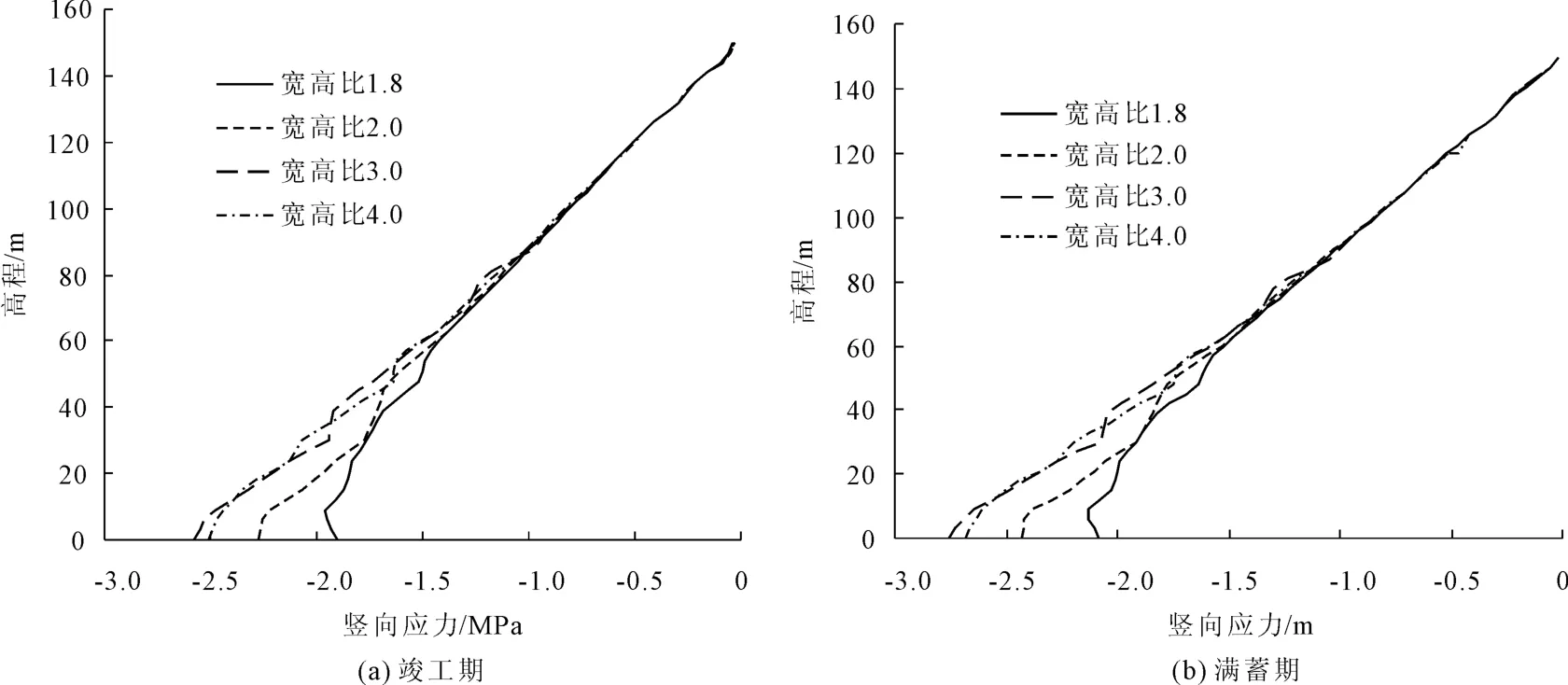
图4 坝体最大断面坝轴线竖直向应力分布图
通过对坝轴线剖面竖向应力的分布情况的研究,蓄水期在岸坡部位,无论是宽河谷还是窄河谷,应力等值线均会受到岸坡约束的影响呈现一定拱形。从分布规律看,宽河谷与窄河谷是基本一致的。在河床部位,由于河床宽度较窄,宽高比1.8和2.0两种方案坝下部的应力等值线拱形较为明显,在坝底部几乎没有平直段,而宽高比3.0和4.0两种方案的应力等值线在河床部位基本是平直的,说明宽高比大于3.0时,河床部位堆石体受两岸边坡约束的影响小。
以上分析表明,宽高比对坝体沉降的影响主要体现在河谷拱效应影响坝体中下部的应力水平,进而影响坝体的变形分布及变形量。在本例的U型河谷中,当宽高比大于3.0后,由于河床较宽,河谷拱效应对坝体中下部应力水平的影响小,故对坝体的沉降变形的影响也较小。
2.2 宽高比对坝轴向位移的影响
由于两岸对称,坝轴线位移等值线以河谷中心线对称分布。坝轴向位移值随宽高比增大而增大,但其对极值的影响较小,宽高比由1.8增大到4.0时,位移极值仅由10.9 cm增大到12.7 cm(见图5)。从轴向位移分布规律看,不同宽高比下轴向位移的分布规律大体一致,位移极值点的位置也基本相同,发生在约3/4坝高处,不同的是宽高比越大,轴向位移梯度越小,当宽高比大于3.0时,河床中部较大范围内的轴向位移接近零。从以上分析可知,对于同样的岸坡,河谷宽度的变化对坝体轴向位移的影响较小。
2.3 宽高比对上游坝面法向位移的影响
图6为蓄水引起坝体上游面法向位移沿高度的分布图,由图6可知,不同宽高比情况下,上游面法向位移的分布规律基本一致,位移最大值均发生在中部偏下位置(约62 m高程)。图7为宽高比与上游面法向位移极值的关系曲线,宽高比增大,河床部位坝体受岸坡的约束减小,上游坝面法向位移也随之增大,在宽高比小于3.0时,宽高比对法向位移值的影响较为明显。随着宽高比的增大,影响逐渐减小。根据这个趋势,随着宽高比的进一步增大,坝体上游面的法向位移将基本趋于稳定。
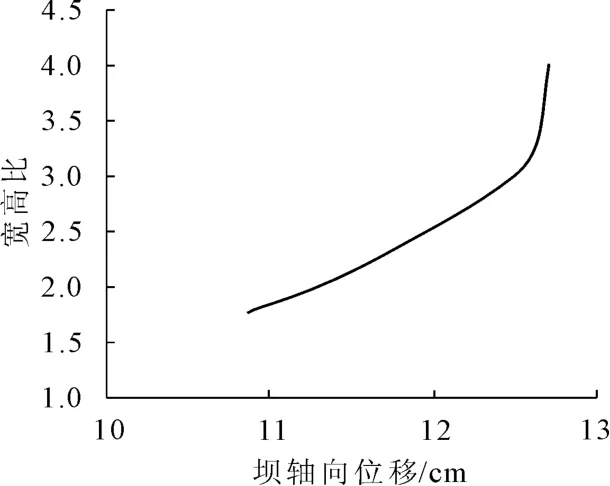
图5 宽高比与最大坝轴向位移的关系曲线
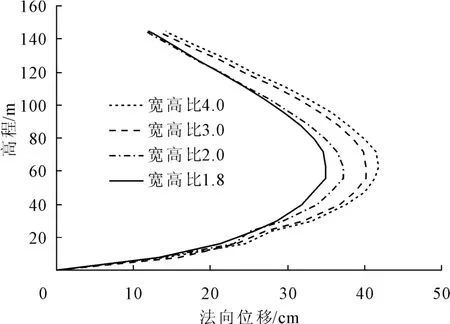
图6 坝体上游面法向位移(蓄水)

图7 宽高比与坝上游面法向位移
3 结 语
本文采用三维非线性有限元法,对不同宽高比下的面板堆石坝应力变形进行数值模拟,分析了宽高比对面板堆石坝坝体变形特性的影响,得出以下认识:
(1)坝体的沉降和上游面法向位移均随着宽高比的增大而增大。当宽高比小于3.0时,坝体沉降和上游面法向位移受宽高比影响较大;当宽高比大于3.0时,坝体沉降和上游面法向位移对宽高比并不敏感;
(2)宽高比对坝体轴向位移有一定影响,但影响较小。
(3)宽高比对坝体沉降的影响主要是由于狭窄河谷形成的拱效应降低了堆石体中的竖向应力,进而减小了坝体的沉降。河谷越窄拱效应越明显,但当宽高比大于3.0,这种拱效应基本消失。
由于本文研究的面板坝位于一特定形状的岸坡,且岸坡地形变化较缓,故本文的结论并不具备普适规律。对于不对称河谷或岸坡地形有突变等复杂的河谷地形,其坝体的变形可能会出现不同的规律,有必要对其展开进一步的研究。
[1] 杨启贵,刘 宁,孙 役,等.水布垭面板堆石坝筑坝技术[M].北京:中国水利水电出版社,2010.
[2] 宋文晶,王彭煦.河谷地形对面板坝防渗体系安全性的影响[J].水力发电学报,2008,27(4):94-100.
[3] 周 伟,常晓林,胡 颖,等.考虑拱效应的高面板堆石坝流变收敛机制研究[J].岩土力学,2007,28(3):604-608.
[4] 朱 晟,欧红光,殷彦高.狭窄河谷地形对200 m级高面板坝变形和应力的影响研究[J].水力发电学报,2005,24(4):73-77.
[5] 程 嵩,张 嘎,张建民,等.河谷地形对面板堆石坝应力位移影响的分析[J].水力发电学报,2008,27(5):53-58.
[6] Duncan J M,Byme P M,Wong K S,et al.Strength,stress-strain and bulk modulus parameters for finite element analysis of stresses and movements in soil masses[R].Berkeley:University of California,1980.
[7] 孔德志,朱俊高.邓肯一张模型几种改进方法的比较[J].岩土力学,2004,25(6):971-974.
- 水利与建筑工程学报的其它文章
- 施工方法对整体式闸室墙后土压力的影响分析

