基于压电悬臂梁的振动能量获取装置的建模及数值仿真
周 璇 王 海 李 晗 王 战 夏小品
(安徽工程大学机械与汽车工程学院,安徽 芜湖 241000)
1 引言
现今人们对环境问题格外重视,无线传感器网络的研究正受到越来越多的关注,研究内容分布也非常广泛,涵盖了从理论到实现、从节能到安全等多个方面。随着微电子和微机械技术的进步,电源对传感器节点使用性能的影响也越来越大,供电问题是无线传感器网络的核心问题之一,因此电源的能量自供给是一种重要的发展趋势。
振动是一种广泛存在于日常生活当中的现象,特别是在道路、桥梁或有大型机械工作的场合中,因此振动能具有广泛的来源。振动能量采集就是采集机械振动能,并将其转换为电能,无需电池,就可使传感器正常工作的一种能量采集技术。振动能量采集的方法主要有三种:压电式、电磁式和静电式。这三种方法适用于不同的场合,可根据无线传感器网络节点使用场合的不同选择一种或多种组合使用。其中,压电式发电具有较多优势:可以直接产生可用的电压;结构设计限制较少;机械阻尼系数较小等等[1]。
许多传统的压电获能器采用的是单压电晶片悬臂梁结构,但是其发电量较小,难以满足无线传感器节点的用电要求,所以现在研究的多为双压电晶片悬臂梁结构。国防科技大学的邓冠前等建立了压电双晶片悬臂梁的仿真分析模型,研究了不同结构尺寸的晶片对发电性能的影响[2]。国外的JyotyK等人也对压电双晶片获能器进行了研究,并在悬臂梁末端置一质量块来降低其谐振频率,提高其输出功率[3]。本文在单质量块基础上又增加了两个质量块,建立其数学模型并进行仿真分析,以研究不同质量块对输出电压的影响。
2 压电悬臂梁的结构设计
悬臂梁常采用梁一端固支,另一端自由的方式,这样系统最容易获得最大挠曲与柔顺系数,也就是说容易产生弯曲变形,而一端固支,也保证了自由振动时只会产生弯曲变形,扭转变形极小,因此保证了转化效率;在悬臂梁系统自由端加三个质量块以降低结构固有频率,提高振幅,增大PZT材料的应力应变以提高能量输出,此处选用镍质量块。 PZT薄膜是现阶段在MEMS领域应用最广泛的压电材料,相比于其它压电材料,PZT的优点在于:压电常数、机电耦合系数较大,制造工艺相对成熟,可与MEMS结构良好兼容,成形工艺好,成本低廉等,因此本设计选用的压电是材料是PZT-5A,并在上下压电陶瓷表面镀一层银作为电极。
由于压电陶瓷硬且脆变形量小,通常将其粘贴在金属片上一起构成压电振子,此处选用铜片。虽然越薄的结构越能满足低频谐振的要求,但其输出电压和转换功率都会下降。PZT层的厚度是影响输出电压和转换功率的重要因素,因此在结构设计时应尽量则加PZT层的厚度,以获取较高的能量。为了得到尽可能低的谐振频率,增加质量块的厚度是不错的选择,但考虑到随着质量块长度、厚度的增加,在梁的末端会形成很大的负荷,这会导致梁的大幅度弯曲甚至断裂,因此通常选择质量块的长度为梁长度的1/6-1/3[4]。厚度值不大于其长度为宜,一般来讲,这样的结构即可以满足低谐振频率的要求,又能保证不过于影响压电悬臂梁的弯曲变形。综上所述设计悬臂梁尺寸如表1所示:

表1 压电悬臂梁尺寸参数及材料基本属性
在ANSYS中建立模型如图1所示

图1 压电悬臂梁模型
3 压电悬臂梁的理论分析
为方便计算将压电悬臂梁简化为如图2所示的等效振动模型:
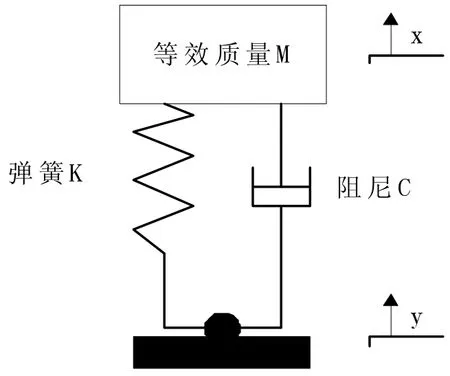
图2 压电悬臂梁等效振动模型
本文设计的压电悬臂梁的长度远大于其厚度故此处做欧拉-贝努力梁处理,忽略剪切变形和转动惯量对梁的影响。
对于图(1)给出的悬臂梁,自由振动的控制方程为:

式中ρ为单位长度的质量,EI为抗弯刚度。
由于工程中遇到的实际结构比较复杂,且工作频率主要是一阶共振频率故本文采用瑞利—里兹法来求梁的基频谐振频率。

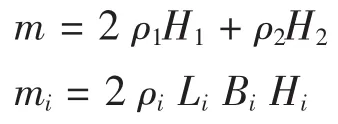
Et为结构整体的等效刚度;B是梁的宽度;L是梁的长度;H1是上层PZT的厚度,H2是Cu层的厚度;H3=H1是下层 PZT 的厚度; ρ1、 ρ2、 E1、 E2是 PZT 层和 CU 层的密度和杨氏模量; Li、 Bi、 Hi、 ρi为质量块i的长、宽、高和密度。
与基频对应的振型函数为


压电系统的总能量由转换的电量、动能、弹性能、机械损耗四部分组成,其关系式如下

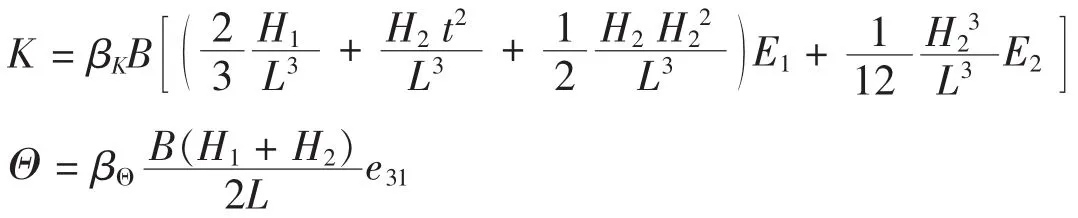
式中设M为系统有效质量,m1、m2为上PZT层质量和Cu层质量mi为质量块i的质量,u(t)为外载荷 F(t)作用在质量块M上时产生的位移;K为弹簧刚度,η为阻尼系数,Θ、Vp(t)分别为压电单元的等效压电系数、两表面电压,βM、βK、βΘ由Rayleigh-Ritz方法导出;e31为压电系数[5]。
通过计算最终得到压电振子的输出电压为:
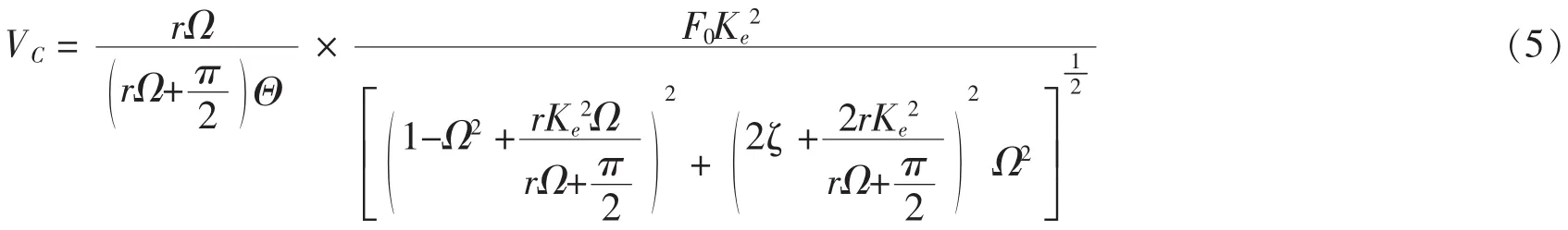
式中F0为载荷的幅值、r为电阻、Ω为标准化频率为机电耦合系数。
4 ANSYS分析
4.1 静力学分析
压电振子的静力学分析主要用于分析悬臂梁压电振子结构因稳态外载荷而引起的应力、应变、位移和电压,它不考虑惯性和阻尼的影响,也不考虑载荷随时间的变化。通过静力分析可以研究压电振子的结构参数对应力、应变、电压的影响规律,从而为压电振子的优化设计提供依据。
在 ANSYS软件中,用于压电分析的单元主要有 PLANE13,SOLID5和 SOLID98,本文中压电陶瓷的单元类型采用SOLID5,金属片的单元采用SOLID45。压电振子弯曲变形后会在压电陶瓷片表面形成一定的电压,陶瓷片表面为一等势面,须进行电压耦合,即在载荷定义里的施加电压边界条件,这是压电分析的关键的一步。用ANSYS软件求解得到压电振子的电压分布云图如图3所示
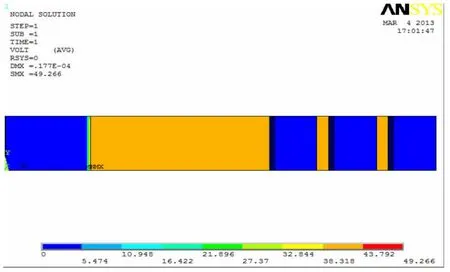
图3 压电悬臂梁静力学分析
通过上图可以看到压电晶片上已经有电压分布,且最大电压值为49.266V。
4.2 模态分析
实际应用当中振动频率范围广泛,某些频率下准静态假设并不成立。为了解系统在高频情况下的响应,对等应变梁进行了模态分析。设备通常在某一频段内振动的,此时,设计与设备匹配的共振频率有利于产生更大的电量。模态分析不但可以用于确定压电振子的各阶固有频率和振型,还可以研究压电振子各参数及质量块对其固有频率的影响规律,进而为设计特定频率的最优压电振子提供依据。分析得到压电振子前3阶振型模态图如图4所示:

图4 压电悬臂梁的前三阶振型模态图
从图4可以看出压电振子处在不同共振频率时有不同的振动形态,得到悬臂梁压电振子前3阶固有频率如表2所示

表2 压电悬臂梁固有频率
由上图可知一阶共振频率附近,悬臂梁上下振动,且振幅在日常振动频率100~300Hz的范围内,这正是我们所需要的悬臂梁的工作状态。
5 谐响应分析
为了显示出三质量块压电悬臂梁的优势文中特与单质量块压电悬臂梁进行对比,用Ansys谐响应分析两中压电悬臂梁产生的电压与振动频率的关系,这也是压电获能分析里较为重要的一步,分析结果如图5,6所示。

图5 单质量块压电悬臂梁电压与频率

图6 三质量块压电悬臂梁电压与频率关系图
从图5可以看出单质量块压电悬臂梁的一阶共振频率约为180 Hz,产生的最大电压值约为36V,从图6可以看出同样的结构三质量块悬臂梁的一阶共振频率约为138Hz,产生的最大电压值约为49V,增加了两个质量块后产生的最大电压较之前增长了近1/3,一般无线传感器节点的电压只需几伏,所以该压电悬臂梁获能装置可以满足实际的使用需求。
结论
目前对于压电悬臂梁获能器的研究多集中在单质量块上,本文在此基础上进行了多质量块压电悬臂梁的研究和分析。研究结果表明三质量块压电悬臂梁产生的电压较单质量块压电悬臂梁增加了近1/3,这将会为无线传感器节点等微电子系统提供更加充足、稳定、持久的电源,这也是本研究的意义所在。
[1] 王矜奉.压电振动理论与应用[M].北京:科学出版社,2011:50-200.
[2] 邓冠前.基于压电陶瓷的振动能量捕获关键技术研究[D].长沙:国防科技大学,2008.
[3] 袁江波.压电俘能技术研究现状综述[J].振动与冲击,2009,28(10):36-42.
[4] 褚金奎.收集环境振动能微压电悬臂梁的制作工艺与测试[J].纳米技术与紧密工程,2011,9(1):1-5.
[5] 李凯威.能量收集技术[M].南京:东南大学出版社,2011:10-100.

