弧底梯形明渠临界水深的简化计算法
滕凯,张丽伟
(1.齐齐哈尔市水务局,黑龙江齐齐哈尔 161006;2.齐齐哈尔市河道管理处,黑龙江齐齐哈尔 161006)
弧底梯形明渠临界水深的简化计算法
滕凯1,张丽伟2
(1.齐齐哈尔市水务局,黑龙江齐齐哈尔 161006;2.齐齐哈尔市河道管理处,黑龙江齐齐哈尔 161006)
弧底梯形断面明渠临界水深计算需完成高次方程求解,无法直接获得。针对目前传统算法及近似算法存在的计算繁琐、成果精度不高,利用微机编程获解又不便于基层工程技术人员应用等问题,通过对弧底梯形断面明渠临界水深计算公式的数学变换,采用优化拟合的方法,以标准剩余差最小为目标函数,在工程实用范围内,经逐次逼近拟合获得了计算简捷、成果精度满足工程设计要求的简化计算公式,具有一定的实际推广意义。
弧底梯形断面;临界水深;优化拟合;近似计算
弧底梯形明渠不仅具有较好的水流条件,断面曲线平滑,有利于渠面衬砌机械化施工的连续作业[1-3],而且弧底所形成的反拱式结构,更适应北方寒冷地区因渠底土体高含水量所产生的冻胀变形及冻害破坏[4-6]。因此,该种断面形式也越来越广泛地被应用于水利水电供排水工程[7-8]。由于弧底梯形明渠断面临界水深计算涉及高次方程求解问题,常规的试算法、迭代法及图表解法[9]或是计算过程繁复,或是求解成果精度不高,不便应用;而由计算机编程求解又不便基层工程技术人员实际操作[10-13]。故文献[14]通过迭代法并经适当简化后获得了该种断面临界水深的简化近似计算式,具有一定的实际意义。但由于该方法引入的中间变量参数较多,实际计算仍显不够简捷,而且适用范围较小(1.0≤m≤4.0,m为渠道坡比系数),对于设计过流量较小的衬砌式渠道,即当0.3≤m<1.0时,其最大计算误差达8.27%。为了进一步改进该种断面临界水深的求解计算方法,本文采用优化拟合的方法,获得了计算过程简捷、求解精度高、使用范围广的简化近似计算式,可在实际工程设计中推广应用。
1 临界水深的基本计算方程
根据水力学原理[15],临界水深的基本计算方程为

式中:Q为渠道流量(m3/s);b为水面宽度(m);A为过水断面面积(m2);α为流速系数;g为重力加速度(m/s2)。
对于弧底梯形断面明渠(断面形式见图1),其临界水深计算可分2种情况:即弧底圆形断面临界水深计算(圆弧内)和弧底梯形断面临界水深计算(圆弧外)。

图1 弧底梯形断面图Fig.1Section of the trapezoidal channel with cambered bottom
1.1 临界水深计算公式判别
由断面过流条件可知,当临界水面线位于弧底曲线与梯形边坡线的切点以下时,临界水深发生在圆弧内,反之,临界水深发生在圆弧外。用数学方法可求得通过切点处的水深为

式中:x为无量纲临界水深;m为明渠边坡比系数。
由式(2)可见,当m→∞时,h→0,切点逐步接近弧底顶点,渠道断面渐进于一条直线;而当m→0时,h→r,渠道断面逐步接近于U形明渠。
1.2 临界水深发生在弧底圆弧内
临界水深发生在圆弧内时,实际为圆形断面临界水深计算问题,其计算公式由文献[16]可得
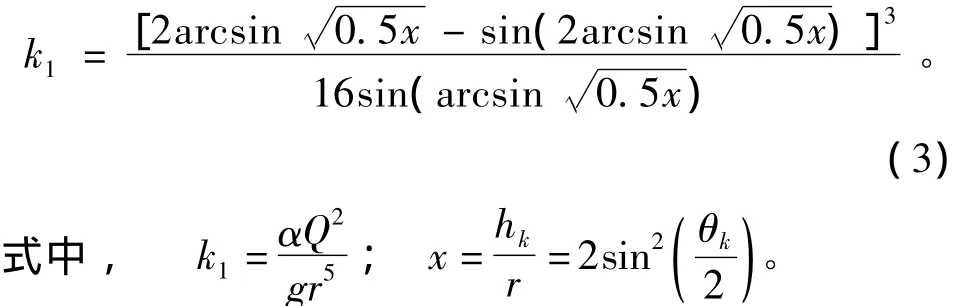
式中:k1为无量纲参数;x为无量纲临界水深; hk为临界水深(m);r为弧底半径(m);θk为临界流时的圆心角(rad)。
1.3 临界水深发生在弧底圆弧外
临界水深发生在圆弧外时,其过水断面积及水面宽可按下式计算:

2 临界水深的近似计算公式
2.1 拟合公式的建立
式(3)及式(6)为含x的高次隐函数方程,无法直接获解。为避免求解高次方程问题,在工程实用范围内(即0.1≤x≤4.0,0.3≤m≤4.0),现假定:当临界水深hk发生在圆弧内及弧底圆弧外时,函数x=f(k1)及x=f(k)可以分别替代式(3)及式(6);并分别展绘x-k1及x-m-k关系曲线,依据曲线关系经数值相关分析,以标准剩余差最小为目标函数[17],即
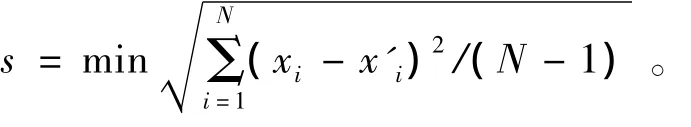
式中N为拟合计算的数组数。
经逐次逼近拟合[18]即可获得如下替代函数,即

式中:B为中间变量;Q0为水面线通过切点情况下的渠道过流量(分界流量,m3/s);由式(2)与式(7)联立即可求得

2.2 拟合公式的精度分析
为比较式(7)与式(3)、式(8)与式(6)的拟合精度,在给定的实用参数范围内,取不同的mi和xi值即可分别由式(3)及式(6)计算出与之相对应的k1i或ki,再将k1i代入式(7)、ki代入式(8)求得与之相对应的x'i,并由式(11)完成拟合相对误差计算:

式中:zi为与xi相对应的第i(i=1,2,3,…,n)点拟合相对误差;n为拟合计算的点数。
由上述计算成果,即可获得任意边坡比m,当0.1≤x≤4.0情况下的相对误差最大值,并由此完成误差包络图绘制,见图2。
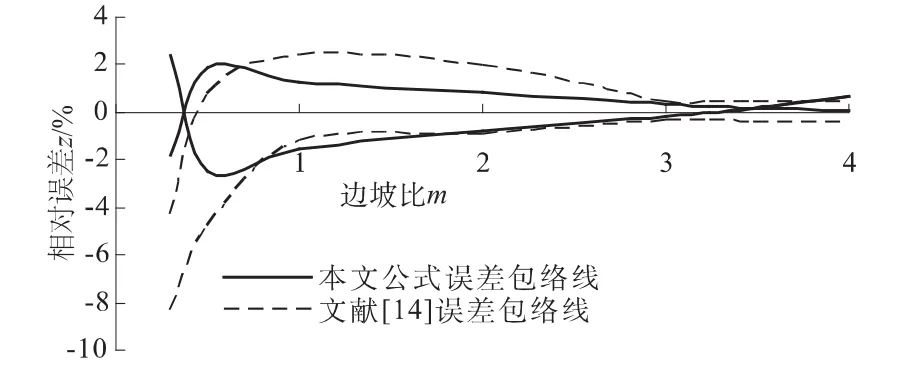
图2 拟合误差包络线Fig.2Envelopes of fitted errors
由图2可见,当0.1≤x≤4.0,0.3≤m≤1.0时,本文式(7)、式(8)的最大计算相对误差为2.47%,而文献[14]的最大计算相对误差为8.27%,是本文的3.35倍;当0.1≤x≤4.0,1.0≤m≤4.0时,本文式(7)、式(8)的最大计算相对误差为1.53%,而文献[14]的最大计算相对误差为2.24%,是本文的1.46倍。可见,本文公式具有较好的计算精度。
3 应用举例
选文献[14]算例:已知某输水渠道过流量Q= 40.0 m3/s,弧底半径r=2.5 m,边坡比系数m= 1.0,试计算渠道的临界水深hk值。
解:根据已知参数,可求得:

精确解为hk=2.388 m,本文公式计算相对误差为0.88%,文献[14]的计算相对误差为1.06%。
4 结语
本文针对目前弧底梯形断面临界水深计算方法存在的问题,通过采用多参数优化拟合的方法,获得了表达形式相对简单且具有较高拟合精度的近似计算公式,实际工作仅借助计算器即可完成解算,适于广大基层工程技术人员应用。通过应用举例计算分析表明,本文公式计算方法简捷,成果精度可靠。
[1]杨彬.弧底梯形渠道全断面振捣连续滑膜衬砌机设计研究[J].陕西水利,2010,(6):91-92.(YANG Bin.Design of Lining Machine for the Continuous Synovial Membrane for Trapezoidal Channel Section with Cambered Bottom[J].Shaanxi Water Resources,2010,(6): 91-92.(in Chinese))
[2]王虎.不同断面形式防渗渠道的应用效果[J].防渗技术,2002,(3):31-33.(WANG Hu.Results of the Application ofAnti-seepageChannelswithDifferent Cross-section Patterns[J].Technique of Seepage Control,2002,(3):31-33.(in Chinese))
[3]李艳玲.弧底梯形混凝土衬砌渠道施工技术[J].山西水利科技,2011,(1):65-66.(LI Yan-ling.Techniques of Constructing Channels with Trapezoidal Concrete Lining with Cambered Bottom[J].Shanxi Hydrotechnics,2011,(1):65-66.(in Chinese))
[4]银俊梅.弧底梯形渠的冻胀试验研究[J].中国农村水利水电,2001,(12):140-143.(YIN Jun-mei.Frost Heave Test for Trapezoidal Channels[J].China Rural Water and Hydropower,2001,(12):140-143.(in Chinese))
[5]王正中,李甲林,郭利霞,等.弧底梯形渠道衬砌冻胀破坏的力学模型研究[J].农业工程学报,2008,(1):26-31.(WANG Zheng-zhong,LI Jia-lin,Guo Li-xia,et al. Mechanical Model for the Damage of Trapezoidal Channel with Cambered Bottom Caused by Frost and Heave[J]. Transactions of the Chinese Society of Agricultural Engineering,2008,(1):26-31.(in Chinese))
[6]宋玲,余书超.弧底梯形渠道受力特征及设计方法研究[J].人民黄河,2010,(8):128-129.(SONG Ling,YU Shu-chao.Forces on and Design Methods of Trapezoidal Channels[J].Yellow River,2010,(8): 128-129.(in Chinese))
[7]冯金祥,朱勤创.弧底梯形断面在宝鸡峡灌区应用的效益[J].防渗技术,2001,(2):33-35.(FENG Jinxiang,ZHU Qin-chuang.Application Results of Trapezoidal Section with Spherical bed in the Baojixia Irrigation Area[J].Technique of Seepage Control,2001,(2):33 -35.(in Chinese))
[8]王文龙.弧底梯形断面在夹马口灌区续改工程中的应用[J].吉林工程技术学院学报,2004,(3):56-58. (WANG Wen-long.Application of Trapezoidal Section with Spherical bed in the Improvement Works of Jiamakou Irrigation Area[J].Journal of Jilin Engineering and Technical College,2004,(3):56-58.(in Chinese))
[9]董为民,赵小利,刘卫华,等.底部含圆弧的梯形断面防渗渠道的水力计算[J].水利与建筑工程学报,2005,(3):54-57.(DONG Wei-min,ZHAO Xiao-li,LIU Wei-hua,et al.Hydraulic Calculation of Seepage Control Canal with Cross Section of Trapezium with Circular-spherical bed[J].Journal of Water Resources and Architectural Engineering,2005,(3):54-57.(in Chinese))
[10]杨茂松,马子普.一种弧底梯形明渠临界水深的快速解法[J].吉林水利,2011,(11):21-23.(YANG Maosong,MA Zi-pu.A Rapid Solution in Calculating Critical Depth for Open Trapezoidal Channel with Cambered Bottom[J].Jilin Water Resources,2011,(11):21-23. (in Chinese))
[11]赵晨.U形及弧底梯形渠道断面水力计算的搜索法与程序[J].水利与建筑工程学报,2006,(3):82-84. (ZHAO Chen.Searching method and Procedures of the Hydraulic CalculationforU-shapedandTrapezoidal Channel Cross-section with Cambered Bottom[J].Journal of Water Resources and Architectural Engineering,2006,(3):82-84.(in Chinese))
[12]孙铁蕾.EXCEL在常用明渠均匀流水力计算的应用[J].水利规划与设计,2006,(5):71-72.(SUN Tielei.Application of EXCEL to the Hydraulic Calculation of Common Open Channel with Uniform Flow[J].Water Resources Planning and Design,2006,(5):71-72. (in Chinese))
[13]成铁兵.弧底梯形及弧角梯形断面水力计算电算程序[J].杨凌职业技术学院学报,2008,(3):23-25,29. (CHENG Tie-bing.Computer Calculation Procedure for the Hydraulic Calculation of Trapezoidal Cross-section with Cambered Bottom and Arc Angle[J].Journal of Yangling Vocational and Technical College,2008,(3): 23-25,29.(in Chinese))
[14]王正中,申永康,彭元平,等.弧底梯形明渠临界水深的直接算法[J].长江科学院院报,2005,22(3):6-8. (WANG Zheng-zhong,SHEN Yong-kang,PENG Yuanping,et al.Direct Formula Calculating Critical Depth for Open Trapezoidal Channel with Cambered Bottom[J]. Journal of Yangtze River Scientific Research Institute,2005,22(3):6-8.(in Chinese))
[15]成都科技大学水力学教研室.水力学[M].北京:人民教育出版社,1980.(Department of Hydraulics of Chengdu University of Science and Technology.Hydraulics[M].Beijing:People’s Education Press,1980.(in Chinese))
[16]刘刚,滕凯.圆形断面临界水深简化近似计算方法[J].水利与建筑工程学报,2011,(6):81-83. (LIU Gang,TENG kai.Simplified Approximate Calculation Method for Critical Water Depth of Circular Section[J].Journal of Water Resources and Architectural Engineering,2011,(6):81-83.(in Chinese))
[17]王慧文.偏最小二乘回归法及其应用[M].北京:国防工业出版社,1999.(WANG Hui-wen.Partial Least Squares Regression Method and Its Application[M]. Beijing:National Defence Industry Press,1999.(in Chinese))
[18]阎凤文.测量数据处理方法[M].北京:原子能出版社,1988.(YAN Feng-wen.Methods of Processing Measurement Data[M].Beijing:Atomic Energy Press,1988. (in Chinese))
(编辑:曾小汉)
Simplified Calculation for the Critical Depth of Trapezoidal Open Channel with Cambered Bottom
TENG Kai1,ZHANG Li-wei2
(1.Qiqihar Municipal Water Affairs Bureau,Qiqihar161006,China; 2.River Management Office of Qiqihar City,Qiqihar161006,China)
In the calculation of the critical depth of trapezoidal open channel with cambered bottom,equations of higher degree needs to be solved.Traditional algorithms and approximation algorithm are complicated with less accuracy,whereas computer programming adopted to solve the equation is inconvenient for on-site application.On the basis of mathematical transformation of the calculation formula,a simplified formula with convenient process is obtained by successive approximation and fitting for engineering practice,with the minimum standard residual difference as objective function.Results of the simplified formula meets the requirements of engineering design,and is worthy of promotion.
trapezoidal section with cambered bottom;critical water depth;optimization and fitting;approximate calculation
TV131.4
A
1001-5485(2013)05-0060-04
10.3969/j.issn.1001-5485.2013.05.014
2013,30(05):60-63
2012-02-24;
2012-03-20
滕凯(1957-),男,黑龙江齐齐哈尔人,高级工程师,主要从事水利防灾减灾及工程优化设计研究,(电话)13704618836(电子信箱)tengkai007@163.com。

