基于空间矢量的滞环电流跟踪控制策略的仿真研究

陈志华，曹以龙

(上海电力学院 电子与信息工程学院，上海 200090)

目前，电流跟踪控制技术很多，其中滞环电流控制是应用最为广泛的方法之一，它属于直接电流控制，具有响应速度快、精度高等优点［1-3］.其主要原理就是利用滞环比较器将反馈电流的变化控制在滞环带以内.但如果其设定的滞环宽度是固定的(传统的滞环控制模式)，那么滞环控制就会存在开关频率不固定、不容易设计输出滤波器等缺点［4］.

空间电压矢量(SVPWM)是近几年的研究热点，具有电压利用率高、可以实现最优开关模式等优点，但同时也存在着计算量大，以及数字化的实现对芯片要求较高等缺点.

本文研究了一种将不定频滞环控制和SVPWM控制相结合的电流控制方式.该方法通过空间电压矢量的实时切换，将电流限制在固定的滞环宽度以内，从而获得良好的电流控制效果.这种控制方法分为定频与不定频两种［5，6］，由于滞环宽度是固定的，故本文采用不定频的滞环SVPWM电流控制方法，并对其在PWM整流器和有源电力滤波器中的应用建立了仿真模型.

1 控制原理

1.1 数学模型及原理

三相无中线VSR拓扑结构如图1所示［7］.

图1 三相无中线VSR拓扑结构

若忽略交流侧电阻，可以得到VSR电压矢量方程为:

式中:U——三相VSR交流侧输出电压矢量;

E——三相电网电动势矢量;

I——三相VSR交流侧电流矢量.

将式(2)代入式(1)中，化简得:

式(3)表明，误差电流矢量的变化率受三相VSR输出电压矢量U，电网电动势矢量E，指令电流矢量变化率的影响.若要获得零误差电流响应，则要求三相VSR输出指令电压矢量 U*应满足:

然而，三相VSR共有8个空间电压矢量Uk(k=0，1，2，3，4，5，6，7)，因此式(3)中的 U 可由U*代替，即:

再将式(4)代入(5)，得

式(6)表明，对于给定的具有零误差电流响应的参考电压矢量U*，可以选择合适的三相VSR空间电压矢量Uk来控制误差电流矢量的变化率 dΔI/dt，进而控制误差电流矢量 ΔI.

图2为不定频滞环SVPWM的三相电流控制原理图.

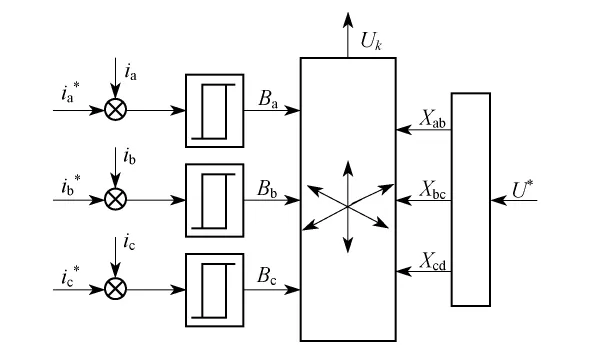
图2 不定频滞环SVPWM的三相电流控制原理

由图2可知，其控制策略是将指令电流与反馈电流通过固定滞环宽度的滞环比较单元，输出相应的比较状态值Ba，Bb，Bc，并通过对指令电压矢量的区域判别，最终由空间电压矢量U*选择逻辑，输出一个合适的Uk，使得三相VSR电流跟踪指令电流［5，6］.

1.2 U*和ΔI区域的划分

图3为指令电压矢量U*的空间区域划分.考虑到 ΔI空间区域划分应有利于 ΔIa，ΔIb，ΔIc的正负极性判别，可以将U*的空间坐标系顺时针旋转π/6，即可获得ΔI空间的区域划分(其中零矢量 U0，U7在图中未标出)［8］，如图 4 所示.

图3 指令电压矢量U*的空间区域划分

1.3 控制规则与Uk的选择

由式(6)可知，指令电压矢量U*和误差电流矢量ΔI一旦确定后，两个矢量的空间区域位置也随之确定.为实现电流跟踪控制，必须选择一个合适的三相空间电压矢量Uk，使得误差电流变化率矢量dΔI/dt与误差电流矢量ΔI的方向始终相反.若设滞环宽度为 Iw，则控制规则如下［5，9-14］:

图4 ΔI空间的区域划分

根据上述规则，不失一般性，可以任意设定矢量U*和ΔI所在区域.若先设定矢量U*在六区，则矢量ΔI在6区，如图5所示.

图5 U*在六区，ΔI在6区

由图5可知，由各空间矢量Uk的终点出发向矢量U*的终点作矢量(用虚线表示)，即为Uk所对应的矢量L(dΔI/dt).

表1 ΔI和U*区域选择与Uk的选择结果

1.4 U*和ΔI的区域检测及Uk选择的逻辑运算

1.4.1 ΔI的区域检测

通过矢量ΔI在a，b，c 3个坐标轴上的分量ΔIa，ΔIb，ΔIc的正负极性判别，可以很容易地确定矢量ΔI所在的区域.再进一步分析可知，矢量ΔI区域实际上可以从三相电流的滞环比较器的输出逻辑中直接判定.

设 ΔIa，ΔIb，ΔIc滞环比较器的输出逻辑变量分别为 Ba，Bb，Bc，且滞环宽度为 Iw，则记:

分析规律可以直接得到ΔI区域判断的逻辑关系为:

式中:RΔI(1)～RΔI(6)——ΔI区域1 ～6 对应的逻辑变量.

当 ΔI位于区域 j时，RΔI(j)=1，否则RΔI(j)=0.

1.4.2 U*的区域检测

考虑式(4)，参考电压矢量U*可由电网电动势矢量E和指令电流变化率相关矢量L(dΔI/dt)合成求得.而E和L(dΔI/dt)均为已知量，通过检测计算，即可得出矢量在坐标a，b，c上投影，，的时域值，也可以通过，，相关极性的判别，确定矢量所在的区域，且记:

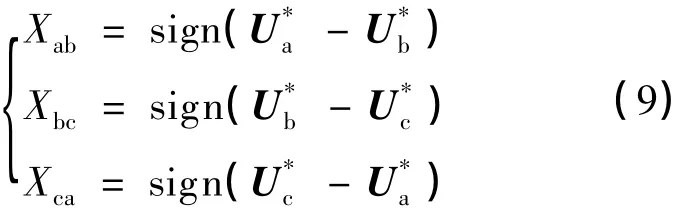
分析规律可获得U*区域判别的逻辑运算关系为:

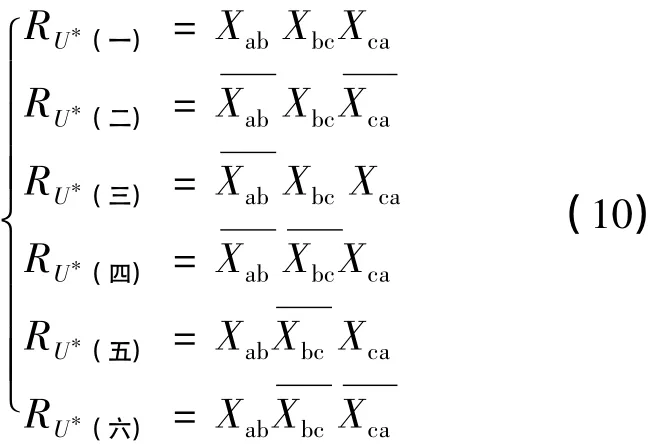
式中:RU*(一)～RU*(六)——U*区域一至六对应的逻辑变量.

当 U*位于区域 i时，RU*(i)=1，否则RU*(i)=0.

1.4.3 Uk选择的逻辑运算

通过相关的逻辑运算，可确定U*和ΔI所处区域，再根据U*和ΔI所处区域的逻辑变量，推得三相VSR基于不定频滞环SVPWM电流控制开关函数Sa，Sb，Sc的逻辑变量算式为:

2 应用模型及仿真结果

本文利用Matlab/Simulink对所阐述的基于空间矢量的滞环电流跟踪控制策略进行建模和仿真，分别验证其在PWM整流器和有源电力滤波器中应用时的正确性.

2.1 在PWM整流器中的应用

基于该控制方法的PWM整流器的仿真模型如图6所示.

图6 PWM整流器仿真模型

该模型的主要模块如下:主电路模块;滞环比较模块;误差电流区域判断模块;指令电压区域判断模块等.

系统主电路仿真参数如下:网侧输入三相电压峰值为311 V;频率为50 Hz;交流侧电感为4 mH;直流侧给定电压为800 V;直流侧电容为1.7 mF.

其仿真波形如图7和图8所示.

图7 网侧电压和电流波形

图8 直流侧电压波形

由图7和图8可以看出，在经过0.02 s即一个工频周期后，网侧电压和网侧电流同相，且是正弦波，谐波含量很小;直流侧电压快速平稳上升至给定的800 V，说明了该系统的快速稳定性.以上两点均验证了该控制策略的正确性和优越性.

2.2 在有源电力滤波器中的应用

基于该控制方法的PWM整流器的仿真模型如图9所示.

模型的主要模块如下:主电路模块;谐波检测模块;直流电压控制模块;滞环比较模块;误差电流区域判断模块;指令电压区域判断模块等.

系统主电路仿真参数如下:网侧输入三相电压峰值为380 V;频率为50 Hz;交流侧电感为4 mH;直流侧给定电压为 800 V;直流侧电容为4.7 mF.

仿真结果分析表明:原来系统的谐波治理率为25.07%;在投入基于该控制策略的有源电力滤波器后，系统的谐波治理率降为4.5%，低于国家规定的标准(5%).由此验证了该控制策略的正确性.

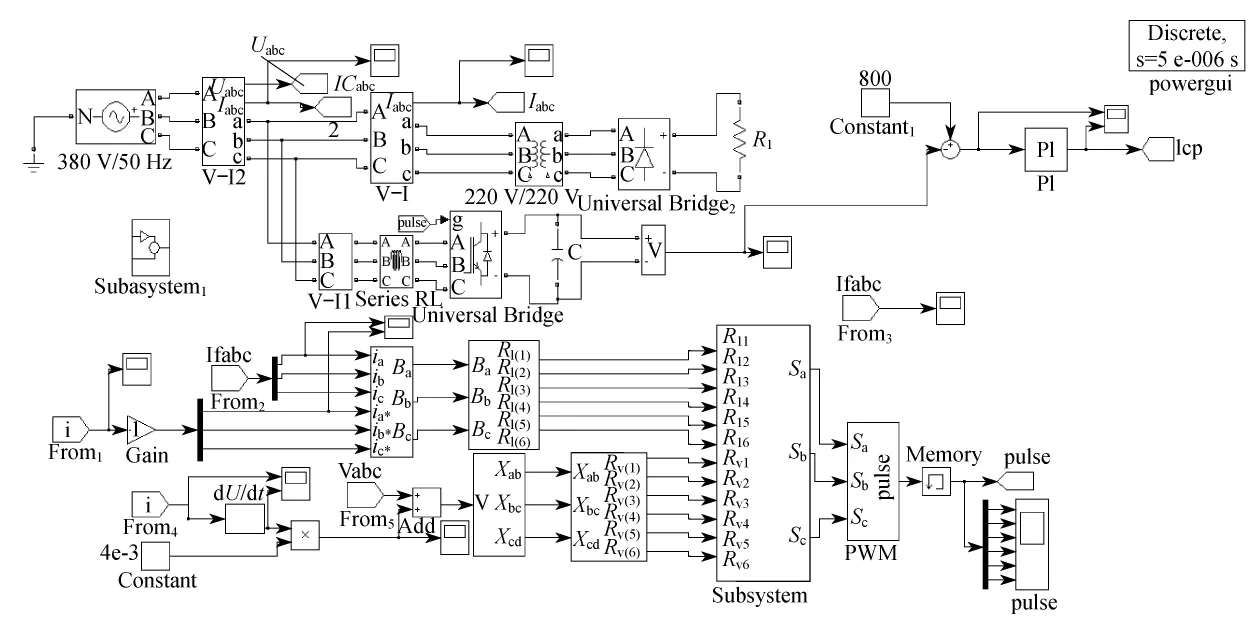
图9 有源电力滤波器仿真模型

3 结语

本文详细阐述了基于空间矢量的滞环电流跟踪控制的原理，分析了指令电压和误差电流的区域判定以及电压矢量的选择方法，并进行了仿真分析.仿真结果验证了该策略的正确性.该方法结合了滞环电流控制和SVPWM电流控制的优点，在实现电流快速跟踪的同时，降低了开关频率，且算法简单，易于实现.

［1］DIXON J W，BOON-TECK OOI.Indirect current control of a unity power factor sinusoidal current boost type three-phase rectifier［J］.IEEE Transactions on Industrial Electronics，1988，35(4):508-510.

［2］宁光岩，赵尉斌.双滞宽变频调速系统的SIMULINK仿真［J］.安徽冶金科技职业学院学报，2004，14(4):38-41.

［3］赵振波，李和明，董淑惠.采用电流滞环调节器的电压矢量控制PWM 整流器系统［J］.电工技术学报，2004，19(1):31-34.

［4］张峰久，惠晶，臧小惠.滞环SVPWM整流器在感应加热电源中的应用［J］.电力电子技术，2005，39(6):63-64.

［5］张兴，张崇巍.PWM可逆变流器空间电压矢量控制技术的研究［J］.中国电机工程学报，2001，21(10):102-105.

［6］程善美.Simulink环境下空间矢量PWM 的仿真［J］.电气自动化，2002，24(3):38-41.

［7］徐文娟，张子林.三相PWM整流器滞环空间矢量控制的研究［J］.变频器世界，2011，8(4):73-76.

［8］SUN Li，KANG Erliang，GAO Hanying.Two-phased SVPWM based on H-bridged structure［J］.IEEE Trans，2003(3):1 730-1 734.

［9］ASIMINOAEI L，BLAABJERG F，HANSEN S.Evaluation of harmonic detection methods for active power filter applications［C］∥20th IEEE Applied Power Electron-ics Conference and Exposition，2005:635-641.

［10］GIRGIS A A，CHANG W B.A digital recursive measurement scheme for online tracking of power system harmonics［J］.IEEE Transactions on Power Delivery，1991(6):1 153-1 160.

［11］RECHKA S，NGANDUI T，XU Jianhong，et al.A comparative study of harmonic detection algorithms for active filters and hybrid active filters［C］∥IEEE PESC，2002:357-363.

［12］ZENG Q，CHANG L，SONG P.SVPWM-based current controller with grid harminic compendation for three-phase gridconnected VSI［C］∥35th Annual IEEE Power Electronics Specialists Conference.Germany:Aachen，2004(35):2 494-2 500.

［13］MALESANI Luigi，MATTAVELLI Paolo，TOMASIN Paolo.High-Performance hysteresis modulation technique for active filters［J］.IEEE Trans.on Power Electronics，1997，12(5):876-884.

［14］张崇巍，张兴.PWM 整流器及其控制［M］.北京:机械工业出版社，2005:226-260.