配电网多级负荷预测中的空间负荷密度指标求解方法
汤 波,刘璐洁,胡 荣,符 杨,李弘扬
(上海电力学院 电气工程学院,上海 200090)
配电系统规划要求负荷预测不仅能预测负荷的总量,还要预测未来负荷增长的位置信息.而目前在中长期负荷预测中应用的算法只能预测总负荷,对负荷的具体空间分布和电压层级分布大多采用简单类比法[1-3],只能进行粗略预测.空间负荷预测弥补了上述方法的不足,不仅提供未来负荷的空间分布信息,而且对规划区域内负荷的地理位置和数值大小等进行预测.空间负荷预测的核心和难点是对待预测区域的用地分析及其负荷密度指标的准确选取.相关研究采用改进型ANFIS算法[2],以及模糊数与多指标灰靶决策理论相结合的方法[3]、模糊理论[4-6]求取负荷密度指标的方法.但大多数算法计算复杂,不适用于工程应用,且只能得到负荷的地理分布而未涉及其电压层级分布.
文献[7]揭示了电力系统负荷预测具有“多维多级”的特点,并提出了多级负荷预测协调的科学问题及解决方法,但该文献仅提出了负荷的层级分布问题,而未对层级负荷如何预测及地理分布预测进行相关研究.
本文通过对多级负荷预测层次关系的分析,采用负荷密度指标法协调负荷空间分布预测、层级预测及总量预测,并针对负荷密度指标求取时影响因素不易量化和计算复杂不易操作的问题,运用灰色关联度理论分类分区求取负荷密度指标,最后用实例验证了该算法的有效性.
1 多级负荷预测及负荷密度指标法
负荷的分布存在地理和电压层级两个维度,如图1所示.
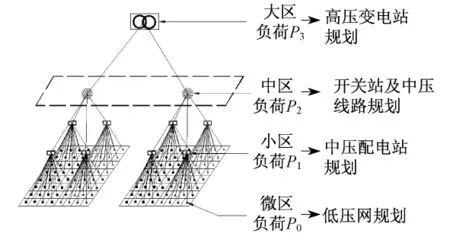
图1 多级负荷预测体系
地理分布上每个小区的负荷并非都是所有微区负荷之和,二者之间存在同时率关系.以此类推,小区负荷、中区负荷间也均存在同时率关系.对应实际配电网,即每座配电站400 V出线最大负荷之和与配电变压器最大负荷间也存在同时率关系,配电变压器负荷之和与10 kV线路负荷之间、10 kV线路负荷之与高压变电站负荷之间均存在同时率关系.由于每一级配电网规划所对应的负荷需求不一致,因此在进行配电网规划时不仅要预测负荷的总量需求,还要预测负荷在地理空间和电压层级两个维度上的分布.
在负荷预测的各种方法中,负荷密度指标法恰能有效解决这一问题,负荷密度指标法是根据单位用地面积或建筑面积的负荷大小进行负荷预测的方法.其数学模型为:
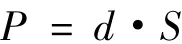
式中:d——负荷密度指标,MW/km2或W/m2;
S——用地面积,km2或 m2.
采用负荷密度指标法预测负荷时,首先需要对待测区域进行用地分析和区域划分,将待测区域按照一定的规则划分成一定数量的各级别区域,然后对每一待测区(可以是微区、小区、中区、大区)进行用地分析,判别其用地性质、用地面积并确定其负荷密度指标.
通过不同地块负荷密度指标的选取,对地块负荷进行预测,考虑不同地块最大负荷的不同时性以预测上一级电网负荷,进而实现逐级负荷预测.
因此,采用负荷密度指标法可以同时协调负荷的总量预测、地理分布预测和层级分布预测,在电网规划时不同电网建设运营层面可根据自身需要预测相应级别的负荷,进而使各级电网规划建设更加匹配合理.
2 负荷密度指标求取模型的建立
负荷密度指标受多种因素的影响,不同性质用地的负荷密度指标的影响因素也不尽相同,甚至差别很大.
例如,通过调研统计分析,影响办公宾馆类负荷密度指标的因素主要有气象因素、待测区属性因素等,每一因素又有若干子因素.
(1)气象因素 负荷密度指标与地区气象变化关系密切,尤其是最高气温和最高气温持续时间,湿度、风力等也是影响负荷密度指标的因素,但各气象因素对负荷密度指标的影响几乎无法用数学模型来描述.因此,可以引入人体舒适度指数[8-11]这一概念,同时结合配电网规划工程实际及数据获取的可行性,来综合考虑气象因素对负荷密度指标的影响.本模型中气象因素仅考虑最高气温及其持续时间、相对湿度3个指标.
(2)属性因素 区域属性因素是决定负荷密度指标的重要因素,一般来说,建筑档次越高,其负荷密度指标也就越高;对同类档次的小区,租赁形式的建筑负荷密度指标要比自有形式的高;而建筑节能水平则与负荷密度指标成反比关系.
表1为部分该类负荷的负荷密度指标及主要影响因素的统计数据.
各影响因素对负荷密度指标的影响程度不同,无法用一个或一组明确的方程表示,因此必须要对各影响因素进行综合评判才能准确确定负荷密度指标[12,13].
灰色系统理论中的灰色关联分析法恰好可以定量分析各因素间相互关联的程度,将多因素的综合评价问题转化为关联度计算,从而较好地解决了这一问题.
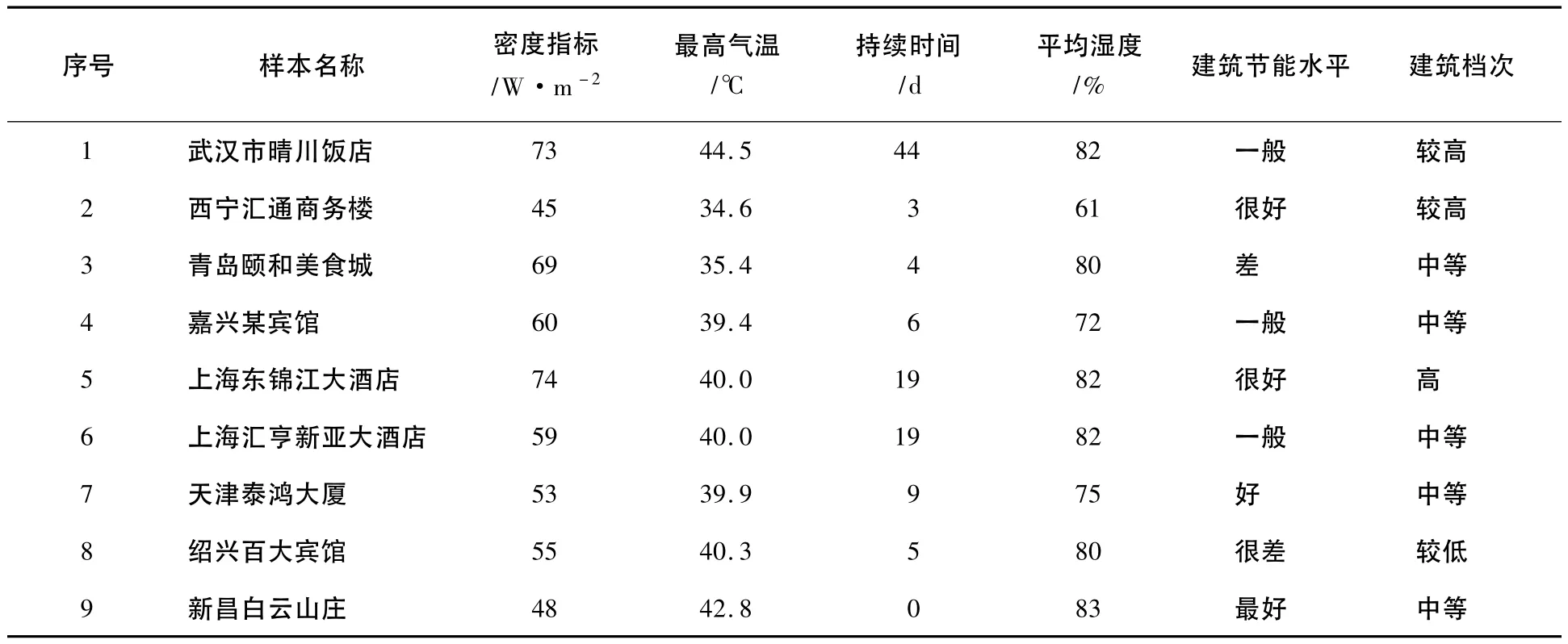
表1 部分区域负荷密度指标调查结果
3 灰色关联理论应用步骤
灰色系统理论[14,15]是邓聚龙教授于 1982年正式提出的一种理论,其中的灰色关联分析法可以定量分析因素间相互关联的程度,目前在多领域得到了广泛应用.
设有m(m>1)个样本,并根据判别影响负荷密度指标的各影响因素,建立代表不同负荷密度指标水平的虚拟样本.这3个虚拟样本序号下标分别为m+1,m+2,m+3;i为所有参评样本(包括虚拟样本)的序号
设影响负荷密度指标的因素共有n(n>1)个,k为影响因素序号,定义影响因素序号下标集合为,那么为第个样本的第k(k∈θ2)个影响因素的评价值.图2为灰色关联分析法求取负荷密度指标的步骤.
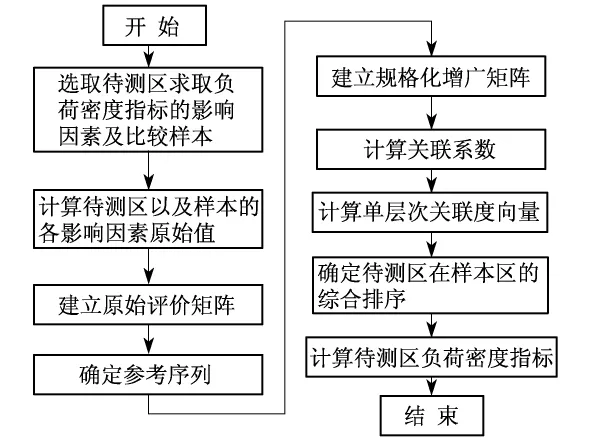
图2 灰色关联分析法求取负荷密度指标的步骤
根据待测区以及比较样本的负荷密度指标各影响因素值,按照图2所示的计算方法采用灰色关联分析法即可得出多因素与负荷密度指标间的关联度,根据关联度可对样本区域和待测区域进行综合排序,根据排序结果即可得到待测区域负荷密度指标的区间值或通过抛物线插值计算得到待测区域负荷密度指标.
4 案例分析
为了验证方法的有效性,以表1数据为例说明本方法的应用步骤,在此将样本数据逐一作为待测区域进行计算.由于模型中属性因素指标为定性指标,不便于各指标之间的比较和运算,为解决上述问题,采用两级比例方法将定性指标转化成定量指标[14],转换方式如图3所示.

图3 定性指标转化为定量指标示意
(1)建立原始评价矩阵:
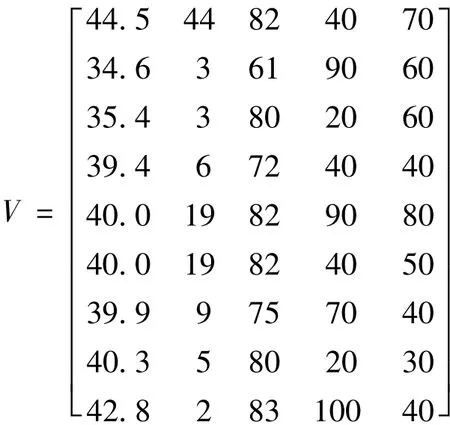
(2)确定参考序列:

(3)建立规格化评价增广矩阵:
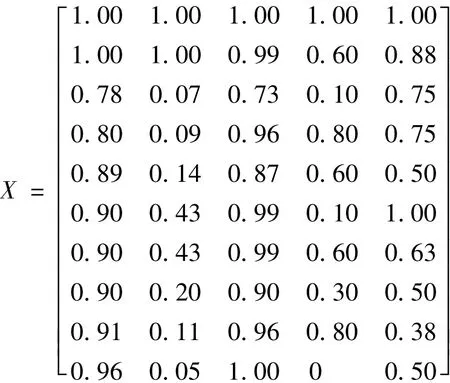
(4)计算单层次的关联度向量:

根据关联度可对样本区域和待测区域进行综合排序,根据排序结果通过抛物线插值计算即可得到待测区域负荷密度指标,如表2所示.
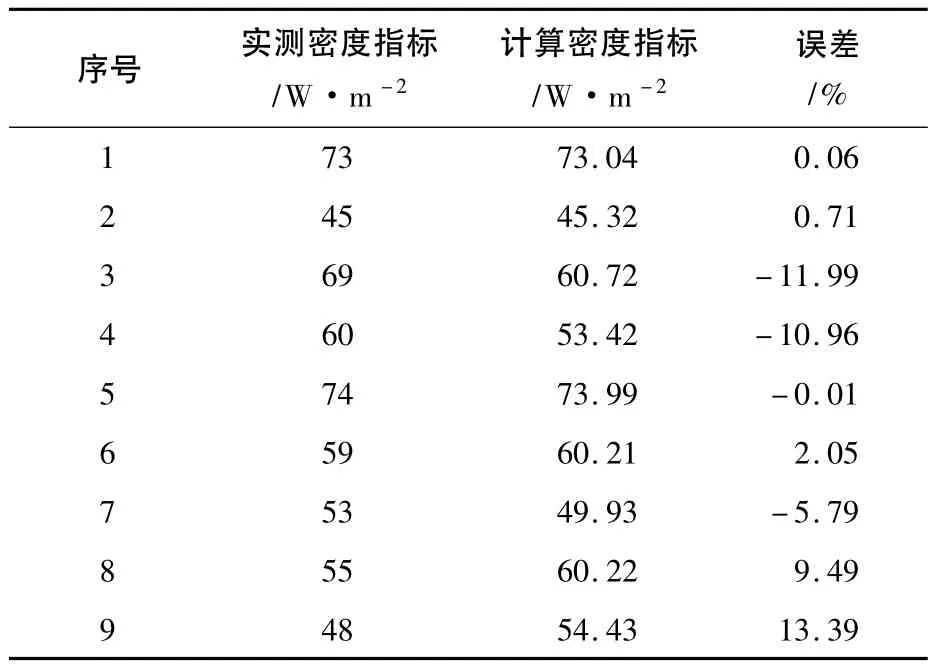
表2 负荷密度指标预测结果
由表2可以看出,预测结果与实际相比,误差大多在10%以内,最大误差为13.39%,能够满足工程实际需要,这说明灰色关联分析法用于求取负荷密度指标是可行的.通过对负荷密度指标预测误差的分析,认为误差主要来源于两个方面,即:各影响因素原始数据获取不够准确;对原始数据的预处理有待加强和模型本身的不严密性.对以上两个方面作进一步完善,能够提高该方法的预测精度和实用性.
5 结语
本文分析了负荷预测的多级性及负荷密度指标的影响因素,构建了负荷密度指标求取模型,提出了采用灰色关联分析法求取负荷密度指标的新方法,并以宾馆类负荷为例,阐述了其应用步骤,实例应用结果表明该方法简单实用,具有较强的实用性和科学性,丰富了配电网负荷密度指标求取的理论.但需在实际操作过程中不断完善样本库,加强对影响因素的量化研究.
[1]黄磊,程浩忠,欧阳武,等.城市高负荷密度地区220/20 kV供电方案研究[J].电力系统保护与控制,2009,37(20):1-6.
[2]周湶,孙威,张昀,等.基于改进型ANFIS的负荷密度指标求取新方法[J].电力系统保护与控制,2011(1):29-34.
[3]吴冰,张筱慧.模糊数与多指标灰靶决策理论相结合的小区负荷预测方法[J].电力系统保护与控制,2011,39(11):124-128.
[4]余贻鑫,张弘鹏,张崇见,等.空间电力负荷预测小区用地分析的模糊推理新方法[J].天津大学学报,2002,35(2):135-139.
[5]符杨,朱兰,曹家麟.基于模糊贴近度理论的负荷密度指标求取新方法[J].电力系统自动化,2007,31(19):46-49.
[6]符杨,曹家麟,谢楠,等.基于模糊综合评判的负荷密度指标选取新方法[J].电网技术,2007,31(18):19-22.
[7]康重庆,牟涛,夏清.电力系统多级负荷预测及其协调问题(一)研究框架[J].电力系统自动化,2008,32(7):34-38.
[8]秦海超,王玮,周晖,等.人体舒适度指数在短期电力负荷预测中的应用[J].电力系统自动化,2006,18(2):63-66.
[9]袁飞,肖晶,卢毅.基于人体舒适度指数的夏季负荷特性分析[J].江苏电机工程,2005,24(6):5-7.
[10]姚艳,孙志能.宁波市电力负荷指标体系之空间负荷密度研究[J].华东电力,2007,35(6):87-90.
[11]王鹏,邰能灵,王波,等.针对气象因素的短期负荷预测修正方法[J].电力系统自动化,2008,32(13):92-96.
[12]CONEJOA J,DELAT S,CANAS M.An optimization approach to multiarea state estimation[J].IEEE Trans.on Power Systems,2007,22(1):213-221.
[13]HWANG KabJu,KIM GwangWon.Spatial load forecasting model for electrical distribution planning[C]∥Proceeding of the 8th Russian-korean International Symposium on Science and Technology,Tomsk,Russian,2004:237-241.
[14]杨伦标,高英仪.模糊数学原理及应用[M].广州:华南理工大学出版社,1993:18-20.
[15]邓聚龙.灰色系统理论教程[M].武汉:武汉理工大学出版社,1990:105-120.

