一种考虑稳定性的动态综合评价新模型❋

吴吉祥，夏靖波，李凡，王 恺

（空军工程大学信息与导航学院，西安710077）

这个非线性规划问题比较复杂，下面给出一种简单的求解方法。该非线性规划的约束条件为两个

线性方程组，目标函数为自变量的最小范数，而广义逆矩阵理论恰好适合于线性方程组的最小范数解的求解。对该非线性规划问题进行形式转换得到

一种考虑稳定性的动态综合评价新模型❋

吴吉祥❋❋，夏靖波，李凡，王 恺

（空军工程大学信息与导航学院，西安710077）

针对动态综合评价需要考虑被评对象的稳定性问题，提出了一种综合考虑指标权重、时间权重和稳定性的动态综合评价模型。定义了稳定因子来表征被评对象指标的稳定程度，采用离差最大化的方法确定指标权重，提出了一种基于极小范数时间权重确定方法。将所提模型应用于军事IP网络评价，结果表明该模型能够把被评对象的稳定性反映到评价结果中。

网络性能评价；动态综合评价；稳定因子；指标权重；时间权重；离差最大化；极小范数

1 引言

评价方法的科学性是客观评价的基础，因此对综合评价方法的研究具有广泛的意义。在现实生活中，针对同一个评价对象，随着时间的发展与数据的积累，人们拥有大量的按时间顺序排列的平面数据表序列，称为“时序立体数据表”。由时序立体数据支持的综合评价问题，参数值是动态的，定义这类评价问题为“动态综合评价”问题。时序多指标评价问题的基本特征是在评价空间和目标空间基础上增加了时间空间，目前的研究主要集中在时序立体数据的归一化方法、指标权重的确定方法和评价结果在时间域上的集结方法［1］等几个方面。投影寻踪法［2］、模糊关联度［3］、模糊综合评价［4］等多种方法被用于解决动态综合评价问题，在评价过程中提出了各种归一化方法、指标权重和时间权重的确定方法［5-7］。在一定程度上，动态综合评价问题得到了较好的解决，被用于工程管理［8］、保险公司业绩［9］和系统风险［10］的评价。但是，评价是一个动态过程，被评对象在该时间域跨度内的稳定性情况同样是一个不可忽视的因素。例如，挑选某人参加某项竞赛的时候，我们不仅考察其多次的成绩水平，同时还会考察其发挥稳定性如何。

同样，作为在一定时间跨度内的评价行为，网络性能评价是一个动态过程，在考虑被评网络域和指标域基础上还要考虑时间域。此外，在被评价时间域内，网络运行质量的好坏不仅取决于各个时刻性能指标的高低，各指标稳定程度作为影响网络运行质量的一个重要方面，在评价过程中也需要综合考虑。因而，在进行网络性能动态综合评价过程中，我们既要关注评价对象的“水平”，同时还要兼顾评价对象的稳定性情况。本文对稳定因子进行了定义，提出了一种考虑指标权重、时间权重和稳定性的动态综合评价模型，并将该模型应用于军事IP网络性能评价实例，验证了模型的有效性。

2 动态综合评价模型

对n个被评价对象（或系统）s1，s2，…，sn，取定m个评价指标x1，x2，…，xm，且按时间顺序t1，t2，…，tN，获得经过预处理的指标数据｛xij（tk）｝，这就构成了一个时序立体数据表。数据的预处理采用全序列极值规范化方法，所有的指标数据均转换为效益性指标。动态综合评价问题是时间、指标、评价对象的三维综合评价问题，把评价对象指标的稳定性考虑进去，动态评价问题将变的更加复杂。从数学角度看，动态综合评价是要通过构造综合评价模型得到评价对象在整个时间段上的综合评价值。综合考虑时间、指标、评价对象和稳定性4个方面建立如下统一的评价模型：

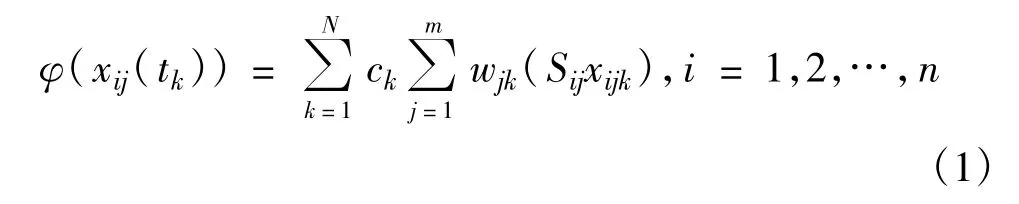
式中，Sij为指标稳定因子，用于体现不同评价对象的某一指标的稳定性；wjk为tk时刻第j个指标的权重系数，用于体现不同评价时刻的某一评价指标对评价结果的贡献度；c＝（c1，c2，…，cN）为时间的权重向量，体现的是时序在评价结果集结中的重要性。该模型在对某一时刻的各指标按照指标权重进行集结之前，先通过指标稳定因子Sij作用于各时刻的指标值，以此来突出稳定因子在评价过程中的作用。再在指标域和时间域对数据进行集结，最终得到评价结果。

稳定因子表征了在整个时间段内，评价对象在不同时刻的评价指标值的稳定程度，定义稳定因子如下：

其中，Dij为第i个评价对象的第j个指标在某一时间段内的方差值。稳定度Sij可以反映出评价对象各个指标在一定时间跨度内的稳定情况，它的取值范围为［1，e］。

设x′ijk为经过稳定因子作用后的指标值，则

稳定因子的作用过程是将第i个评价对象的第j个指标的稳定因子Sij直接乘以该指标在各个时刻的值。

3 基于离差最大化的指标赋权

不同的指标权重确定方法会带来不同的评价结果，一般地，若所有评价对象在某一指标下的差异越小，则说明该指标对决策所起的作用就越小；反之，所有评价对象在某一指标下的差异越大，则说明该指标对决策所起的作用就越大。因此，从对评价对象进行排序或择优的角度考虑，指标值的离差越大应该赋予越大的权重，离差越小就应该赋予越小的权重。特别地，若所有评价对象在某一指标下的值无差异，则此指标对决策将不起作用，可令其权重为零。假定k时刻，第i个评价对象与其他评价对象关于第j个指标的离差用dijk（w）表示，则

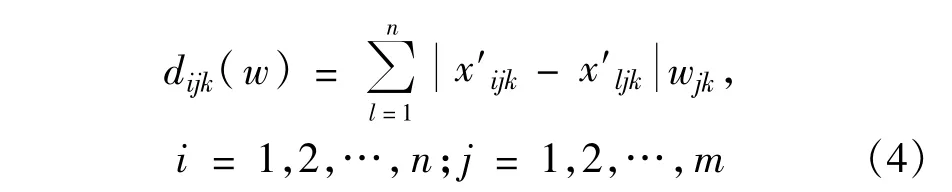
djk（w）表示k时刻，关于第j个指标，所有评价对象的总离差，则有

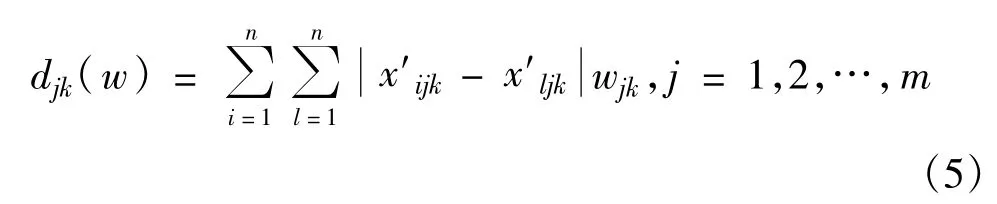
在k时刻为使所有m个指标对所有n个评价对象的总离差达到最大，建立如下线性规划模型：

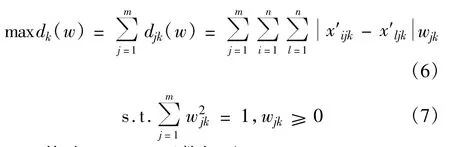
构造Lagrange函数如下：

根据极值存在的必要条件，有

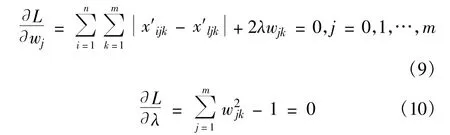
求解并进行归一化后得到

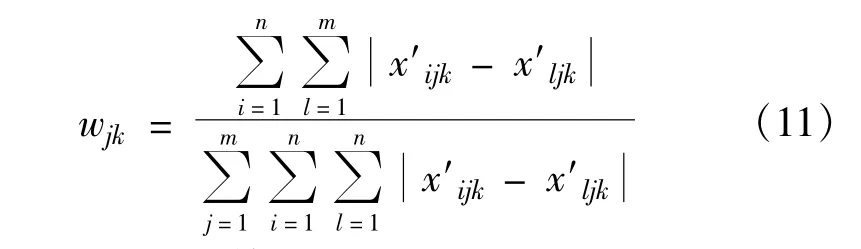
wjk即为k时刻第j个指标的权重系数，该系数因时刻的不同而不同，完全取决于k时刻的指标数据。

4 基于极小范数的时间赋权

科学确定时间权重ck将是得到合理的评价结果的关键。时间权重λk是表明对不同时刻的重视程度，可以根据不同的准则，应用不同的主客观赋权方法来确定。目前，熵值法和方差法是两种主要的时间赋权方法［11］，本文从时间权向量范数最小的角度给出一种时间赋权方法。

时间度η体现了在不同时刻的评价值集结过程中对时序的重视程度，当η接近0时，表示评价者越注重近期数据；当η接近1时，表示评价者越注重前期数据；当η接近0.5时，表示评价者对各个时期数据的重视程度相同。η的具体取值可以参照文献［6］。

极小范数法确定时间赋权的准则是在实现给定时间度η的前提下，寻找一组范数最小的时间权重系数来集结不同时刻的评价值。范数最小代表了在满足不同时刻权重大小次序的前提下，各个时刻权重更加均衡。根据这个思路，抽象出如下非线性规划问题：

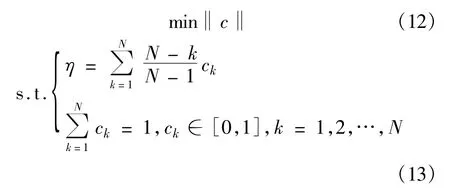
这个非线性规划问题比较复杂，下面给出一种简单的求解方法。该非线性规划的约束条件为两个

线性方程组，目标函数为自变量的最小范数，而广义逆矩阵理论恰好适合于线性方程组的最小范数解的求解。对该非线性规划问题进行形式转换得到

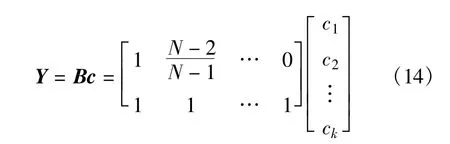
其中，Y＝［η，1］T。利用Moore-Penrose逆矩阵B＋可求得满足约束方程的最小范数解：

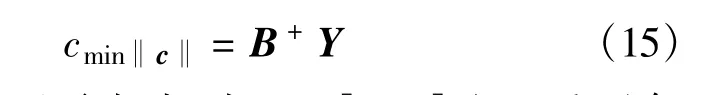
然而，我们还需考虑到ck∈［0，1］这一重要条件。利用式（15）所求得的ck会有小于0或者大于1的情况。因而，在求解过程中须按照以下步骤进行：

步骤1：利用式（15）求解时间权重，如果ck∈［0，1］，则ck即为最终结果；

步骤2：如果存在ck大于1，则设定k时刻时间权重为1，其他时刻时间权重均为0，所得ck即为最终结果；

步骤3：如果存在ck小于0，则将系数矩阵B第一列中小于0的时间权重更新为0，按照步骤1计算ck。

在获得了稳定度Sij、不同时刻的指标权重wjk和时间权重ck之后，即可以按照式（1）对评价对象展开评价。

5 应用举例

根据某军事IP网络管理系统中的统计数据，对A、B、C、D和E 5个被评单位网络进行综合评价，以此来说明文中所提方法的有效性。在选取网络性能指标时应该遵循以下原则：

一是业务性，即要从用户角度考虑业务的所有方面，指标要能反映承载业务的特性；

二是可测性，即选取的指标在现有的条件下能够通过测量获取；

三是全面性，即指标要能全面体现网络性能。

根据上述原则，选取带宽、延迟、丢包率、吞吐量、连通性5个指标。指标数据的来源为网管系统中某段时间3周的统计数据。

首先采用全序列极值规范化方法对原始数据进行规范化处理，具体结果如表1所示。利用表1中经过规范化处理的数据，根据式（2）求得稳定因子Sij，结果如表2所示。根据式（3）采用表1中所求的稳定因子对归一化后的指标数据进行处理，然后按照式（11）求得3个时间各个指标的权重系数，具体如表3所示。

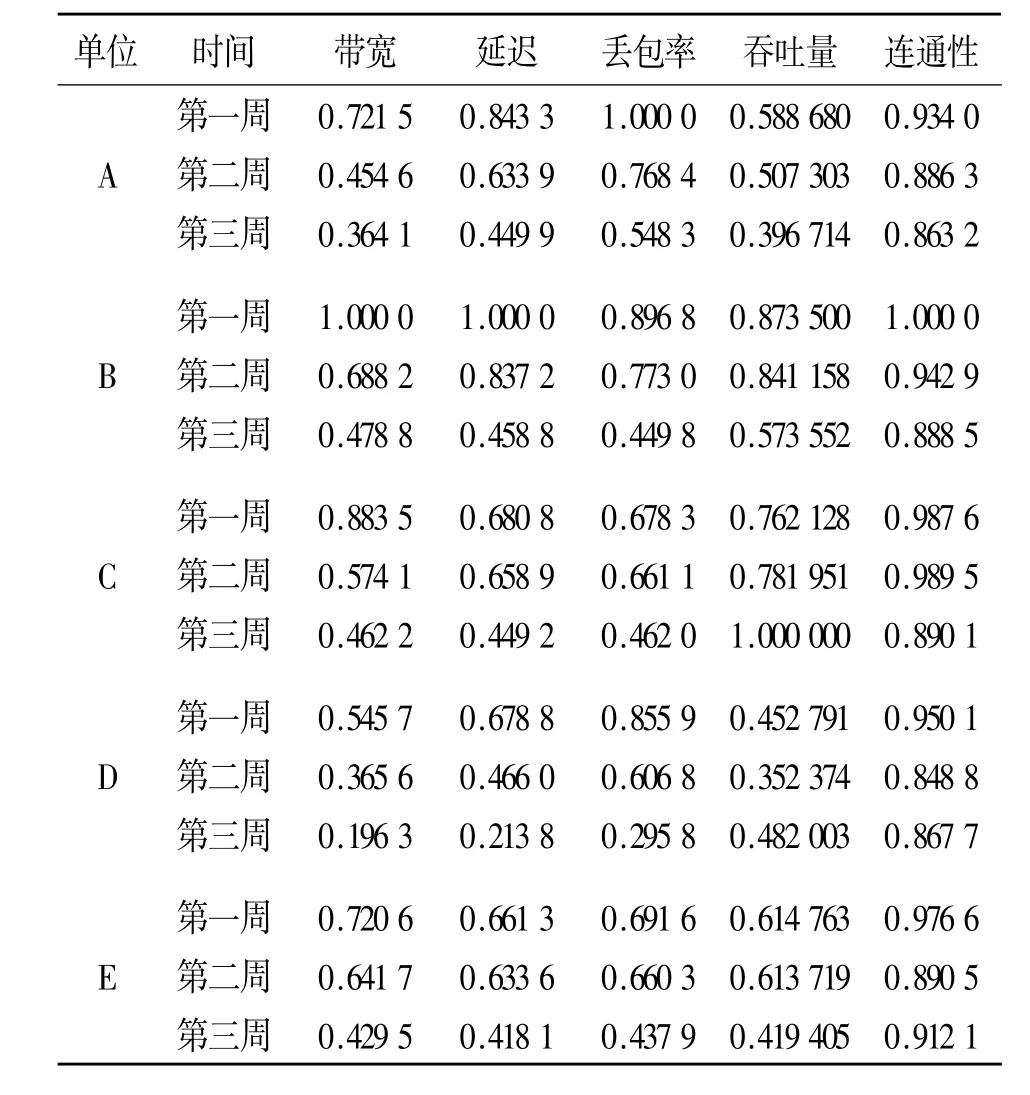
表1 规范化后的数据Table 1 The data after normalization

表2 各指标稳定因子Table 2 The stability factors of attributes

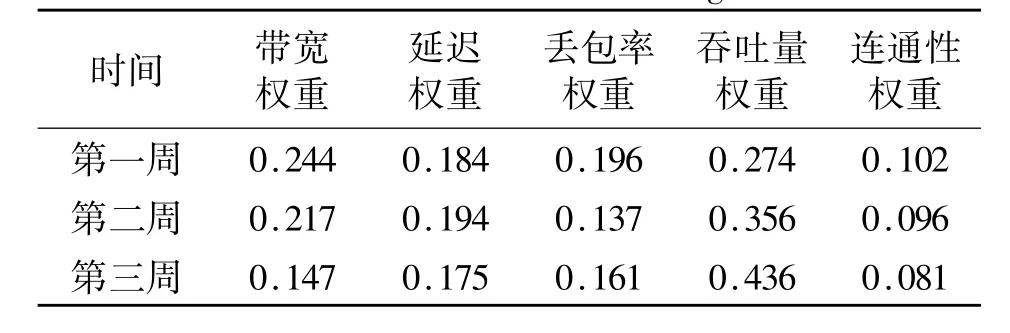
表3 时间权重系数Table 3 Coefficient of time weight

参照文献［6］时间度的标度参考情况，选择η为0.3，即较重视近期数据。由文中给出的基于最小范数的时间权重确定方法，得到3个时段的时间权向量为（0.133 3，0.333 3，0.533 3）。在获得了不同时间的指标权重和各时段的时间权重之后，按照式（1）求得最终的评价值。将本文提出的考虑稳定性的动态综合评价方法与投影寻踪的动态综合评价方法［2］、灰色关联度计算方法［3］、未考虑稳定性的动态综合评价方法［11］进行了对比，具体如表4所示。

表4 评价结果及对比情况Table 4 The evaluation results and contrast

从表4中可以看出，文中所提的方法与其他方法在各个单位网络综合性能排序上主要的不同体现在B与C的次序上。从表1中可以发现，单位C的带宽、延迟、丢包率和吞吐量4个指标的稳定因子均高于单位B的，仅有连通性这一个指标的稳定因子低于单位B。因而，在综合考虑了各单位网络指标稳定性的情况下，B单位与C单位的综合性能排序发生了变化。

6 结论

动态综合评价的方法虽然有很多，但由于各种方法出发点不同，考虑问题的角度不同，解决问题的思路也不同，这就有可能导致不同的评价结果。在一些评价的领域里，被评对象在一定时间跨度内的稳定性情况是动态综合评价必须考虑的一个因素。本文提出了一种考虑稳定性的动态综合评价方法，既关注了评价对象的“水平”，还兼顾了评价对象的稳定性，使得动态综合评价问题的解决更加科学与全面。军事IP网络性能评价的应用实例表明，文中所提的模型能够将被评对象的稳定性情况反映到评价结果中。如何把稳定性这个因素在评价过程中体现得更加科学合理仍然是一个值得探讨的问题。

［1］Huang Y H.Research on the Dynamic Comprehensive Evaluation Based on Information Integrated［C］//Proceedings of 2010 International Symposium on Computer，Communication，Control and Automation.Tainan：IEEE，2010：225-228.

［2］金菊良，汪淑娟，魏一鸣.动态多指标决策问题的投影寻踪模型［J］.中国管理科学，2004，12（1）：64-67. JIN Ju-liang，WANG Shu-juan，WEI Yi-ming.ProjectionPursuit Model for Dynamic Multiple Attribute Decision Problems［J］.Chinese Journal of Management Science，2004，12（1）：64-67.（in Chinese）

［3］樊治平，肖四汉.一类动态多指标决策问题的关联分析法［J］.系统工程，1995，13（1）：23-27. FAN Zhi-ping，XIAO Si-han.A Relation Grade Approach for The Dynamic Multiple Attribute Decision Making［J］.Systems Engineering，1995，13（1）：23-27.（in Chinese）

［4］Wang Y H，Xiao X M，Zhang C C.The Research of Dynamic and Comprehensive Evaluation of Interoperable Trust Based on Fuzzy Comprehensive Evaluation with Variable Weights［C］//Proceedings of 2010 Second International Conference on Computer Modeling and Simulation.Sanya，Hainan：IEEE，2010：569-574.

［5］易平涛，张丹宁，郭亚军，等.动态综合评价中的无量纲化方法［J］.东北大学学报（自然科学版），2009，30（6）：889-892. YI Ping-tao，ZHANG Dan-ning，GUO Ya-jun，et al.Study on Dimensionless Methods in Dynamic Comprehensive Evaluation［J］.Journal of Northeastern University（Natural Science），2009，30（6）：889-892.（in Chinese）

［6］郭亚军.综合评价理论、方法及应用［M］.北京：科学出版社，2007：101-111. GUO Ya-jun.The theory，method and application of comprehensive evaluation［M］.Beijing：Science Press，2007：101-111.（in Chinese）

［7］黄玮强，姚爽，郭亚军.不完全指标偏好信息下的动态综合评价模型与应用［J］.东北大学学报（自然科学版），2011，32（6）：891-894. HUANG Wei-qiang，YAO Shuang，GUO Ya-jun.Dynamic Comprehensive Evaluation Model of Incomplete Index Preference Information and Its Application［J］.Journal of Northeastern University（Natural Science），2011，32（6）：891-894.（in Chinese）

［8］Niu D X，Tian J，Jia r B，et al.Dynamic fuzzy comprehensive evaluation of construction project management［C］//Proceedings of 2011 International Conference on E-Business and E-Government.Shanghai：IEEE，2011：1-4.

［9］Li Shouwei，He Jianmin，Zhuang Yaming，et al.Dynamic Comprehensive Evaluation of Property Insurance Companies′Business Performance［C］//Proceedings of 2010 International Conference on E-Business and E-Government.Guangzhou：IEEE，2010：3916-3919.

［10］Wei G F，Zhang X，Zhang X L.Research on Risk Assessment and Optimization Control of Information Systems Development Based on Improved Fuzzy Comprehensive Evaluation and Dynamic Programming Algorithm［C］//Proceedings of 2010 International Conference on Computational Intelligence and Software Engineering.Chengdu：IEEE，2010：1-5.

［11］郭亚军，唐海勇，曲道钢.基于最小方差的动态综合评价方法及应用［J］.系统工程与电子技术，2010，32（6）：1226-1228. GUO Ya-jun，TANG Hai-yong，QU Dao-gang.Dynamic comprehensive evaluation method and its application based on minimal variability［J］.Systems Engineering and Electronics，2010，32（6）：1226-1228.（in Chinese）

WU Ji-xiang was born in Laiwu，Shandong Province，in 1985.He received the M.S.degree in Communication and Information System from Air Force Engineering University in 2009.He is currently working toward the Ph.D.degree.His research concerns theory of comprehensive evaluation and the evaluation of military communication network.

Email：Jixiang19850126＠163.com

夏靖波（1963—），男，河北秦皇岛人，教授，博士后，主要研究方向为军事通信网络管理与评估；

XIA Jing-bo was born in Qinhuangdao，Hebei Province，in 1963. He is now a professor with the Ph.D.degree.His research concerns management and evaluation of military communication network.

Email：jbxiad＠sina.com

李凡（1981—），男，陕西西安人，工程师，主要研究方向为网络评价；

LI Fan was born in Xi′an，Shaanxi Province，in 1981.He is now an engineer.His research concerns network evaluation.

王恺（1981—），男，河南长垣人，博士，工程师，主要研究方向为军事通信网络评估。

WANG Kai was born in Changyuan，Henan Province，in 1981. He is now an engineer with the Ph.D.degree.His research concerns military communication network evaluation.

A New Dynam ic Com prehensive Evaluation M odel Considering Stability

WU Ji-xiang，XIA Jing-bo，LI Fan，WANG Kai
（School of Information and Navigation，Air Force Engineering University，Xi′an 710077，China）

The stability of evaluated unit need be considered for dynamic comprehensive evaluation.A model of dynamic comprehensive evaluation is proposed which considers attribute weight，time weight and stability factor. The stability factor is defined to denote the stability degree of evaluated unit.The attribute weight is obtained utilizing the method of the maximal deviation.A method of minimum norm is proposed to get the time weight and the process of calculation is introduced.The proposed model is applied to the evaluation of military IP network and the result is affected by result attribute stability.

network performance evaluation；dynamic comprehensive evaluation；stability factor；attribute weight；time weight；maximal deviation；minimum norm

Jixiang19850126＠163.com

TN915

A

1001-893X（2013）05-0548-05

10.3969/j.issn.1001-893x.2013.05.004

吴吉祥（1985—），男，山东莱芜人，2009年获工学硕士学位，现为博士研究生，主要研究方向为综合评价理论、军事通信网络评估；

2012-11-16；

2013-03-12 Received date：2012-11-16；Revised date：2013-03-12

全军军事类研究生资助课题（2010XXX-X88，2011XXX-X23）；陕西省自然科学基础研究计划项目（2012JZ8005）

Foundation Item：The Research Topic of Military Science Graduate Student（2010XXX-X88，2011XXX-X23）；Provincial Natural Science Foundation Research Project of Shaanxi Province（2012JZ8005）

❋❋

Jixiang19850126＠163.com