燃料球体积填充率对2 MW先进高温堆物理特性的影响

李晓恒 陈金根 邹 杨 康旭忠 蔡翔舟 郭 威 梅龙伟 张鸿飞

1（中国科学院上海应用物理研究所嘉定园区 上海 201800）2（兰州大学核科学与技术学院 兰州 730000）

燃料球体积填充率对2 MW先进高温堆物理特性的影响

李晓恒1,2陈金根1邹 杨1康旭忠1蔡翔舟1郭 威1梅龙伟1张鸿飞2

1（中国科学院上海应用物理研究所嘉定园区 上海 201800）
2（兰州大学核科学与技术学院 兰州 730000）

在燃料装载量不变情况下，燃料球体积填充率的变化对于先进高温堆的堆芯物理特性有重要影响。我们运用蒙特卡罗程序MCNP 5对Keff、中子能谱及中子注量率的空间分布进行了研究。计算中，燃料球体积填充率取值范围在最密堆积和最稀堆积之间(0.7405–0.5236)。结果表明，燃料球体积填充率的增加可以提高堆芯的Keff，促使中子能谱更加硬化，使中子注量率峰值所在轴向的位置上升。从而为先进高温堆的设计和计算程序的开发提供理论基础。

先进高温堆，临界，体积填充率，燃料球，中子能谱，中子注量率

核电作为安全、清洁、高效和唯一现实可行的工业化替代能源，在满足人类电力需求和缓解温室气体带来的环境压力方面发挥了重要作用[1]。美国于2003年正式提出先进高温堆(Advanced high temperature reactor, AHTR)的概念，用氟化熔盐作为冷却剂，这类反应堆出口温度可以达到700ºC以上，工作在常压下(小于10个大气压)，属于氟盐冷却高温堆(Floride salt-cooled high temperature reactors, FHRs)中的一种。其继承六种备选的第四代反应堆，第二代、第三代反应堆以及火电站的技术基础与优点：(1) 熔盐堆的熔盐冷却技术、热工水力组件技术和合金结构材料技术；(2) 先进高温堆和高温气冷堆的TRISO燃料颗粒技术和布雷顿循环技术；(3)液态金属反应堆的非能动衰变热排出技术；(4) 第二、三代反应堆的非核岛部分设计；(5) 先进火电站的超临界水能量循环技术等。由于先进高温堆内在的特性，在结合其他反应堆或电站技术和优点的基础上，能够满足新一代核能系统的先进性要求，在技术层面也具有极大的可行性[2,3]。

对于新型大型商业堆的建设，除了实现和完善基础概念设计外，还需要瞄准大型商业堆的应用目标，开展多项新型技术研发和储备。本文针对初始时刻(t=0)，2 MW先进高温堆在总体燃料装载量不变的情况下，研究燃料球(包括铀球和钍球)体积填充率对反应堆相关物理特性参数(如Keff、中子能谱以及中子注量率空间分布等)的影响。

1 模型和计算程序

1.1计算模型

2 MW先进高温堆示意图如图 1所示，由于堆芯中心处中子注量率较高，有利于钍燃料的增殖，所以中心处放置钍球，外围区域放置的是铀球。在构建模型时，对于文献[4,5]中需要近似处理的问题，我们进行了相应的简化。第一，燃料球在壁面处会发生切球现象，但是作为初步研究，我们采用了Massimiliano等人[4,5]的方法，未作处理，忽略这一影响。第二，建模时材料的输入，由于计算时间与计算机计算能力的允许，我们并未采取体积平均法的处理方式，而是依据实物参量建模，从而提高了计算的精度。堆芯活性区由下至上分为三区，高度分别为188、69、50 cm，上部两区为堆芯的卸料区。燃料球间填充着熔盐，活性区上部为卸球管道，以熔盐填充，活性区下部是熔盐区。燃料球体积填充率变大，球间的熔盐流入下部区域；反之，下部区域的熔盐流入球间。所以，堆芯活性区的下边界随着燃料球体积填充率而变化，而188 cm的高度只是我们给出的参考值，总体物理参数设计如表1所示。

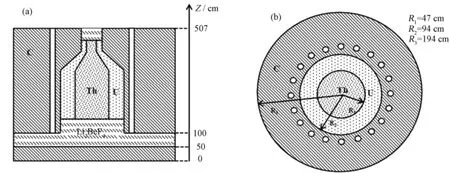
图1 MCNP计算的2 MW先进高温堆的轴向(a)和径向(b)剖面图Fig.1 Elevation view(a) and plan view(b) of the 2 MW AHTR model in MCNP.

表1 2MW先进高温堆的堆芯参数Table1 Main parameters of 2 MW AHTR.

模拟计算中，常用到的几种基本栅元有简单立方栅元(Simple cubic lattice, SC)、体心立方栅元(Body centered cubic lattice, BCC)、面心立方栅元(Face centered cubic lattice, FCC)以及点对点六面柱栅元(Column hexagonal point on point lattice, CHPOP)。表2给出了不同栅元的最大体积填充率及基本栅元中的球数[6,7]。

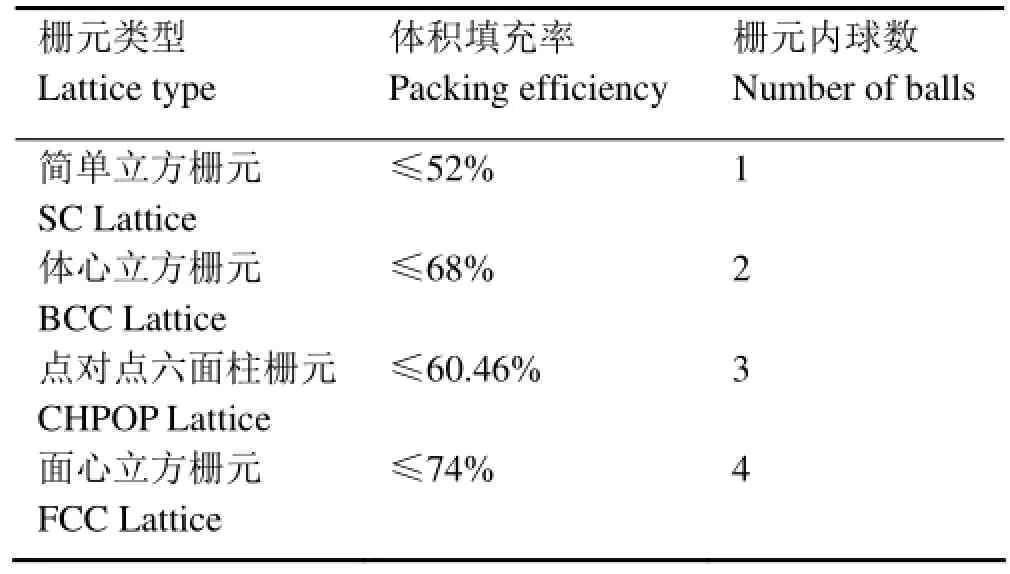
表2 球床堆的基本栅元特性和栅元内球数Table2 Characteristics of base lattice and number of balls.

在上述栅元模型中，只有面心立方栅元给出的燃料球体积填充率(Packing)可以达到最大值74%。所以，计算选取的模型为FCC，可以将可能出现的情况全部覆盖。

1.2程序介绍

MCNP (Monte Carlo N-particle transport code)是由美国洛斯阿拉莫斯国家实验室(Los Alamos National Laboratory)开发的一个通用的蒙特卡罗(Monte Carlo)程序。本文使用的版本是MCNP 5，所用的点截面库为ENDF6版本。MCNP 5是一个大型三维输运程序，可用于计算中子、光子或中子-光子的耦合输运问题，也可以计算临界系统(包括次临界及超临界)的本征值问题。在核能、辐照屏蔽、剂量学和辐射生物学领域均有广泛应用。MCNP 不直接解输运方程，而是通过模拟大量粒子行为并记录它们平均行为的某些特征来得到输运方程的解。MCNP 可以处理任意三维几何结构的问题，几何区的界面可以是平面、 二阶以及某些特殊的四阶曲面(如椭圆环的环面)，其输入文件包括栅元卡、表面卡和数据卡。其中，数据卡又包括材料卡、源项卡、记数卡。利用表面卡和栅元卡对堆芯以及反射层作出精确的几何描述。MCNP 把几何空间分成许多栅元，每个栅元由一个或几个曲面(或平面)围成，栅元内填充以材料。所有栅元都在栅元卡中列出，而表面卡则列出全部平面和曲面，材料卡列出所用全部材料[8]。本文中，由于先进高温堆的燃料与熔盐等材料温度非常高，甚至会达到1050 K，所以运用NJOY程序为MCNP中涉及的材料做了相应的温度库以使计算结果更加精准。

2 结果与讨论

2.1 Keff随燃料球体积填充率的变化

运用MCNP对全堆芯Keff进行了计算，统计区域为整个堆芯。综合以往高温气冷堆及现有先进高温堆的设计、刘时贤等[9]的研究以及燃料球的密度大于熔盐密度的特点，我们总结出以下结论：燃料球会浮在整个堆芯上部，球只能是密集堆积，体积填充率也只能在最密堆积和最稀堆积燃料之间，所以，燃料球体积填充率取值范围在最密堆积(如面心立方)和最稀堆积(简单立方)之间(0.7405–0.5236)。对于采取随机排列方式填充的燃料球，填充系数一般在60.5%出现的概率最高[4,5,9]。所以在60%–61%(最概然的填充系数)附近取很密的点(0.1%取一个点)。

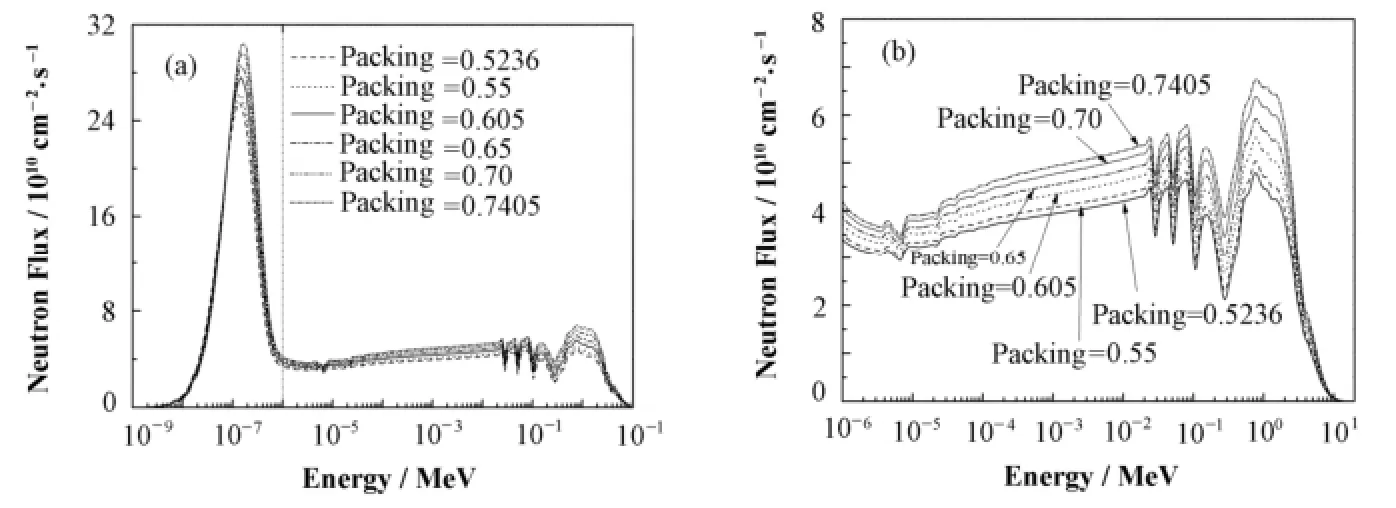
图3 燃料球体积填充率对于中子能谱的影响Fig.3 Neutron spectra as a function of pebble packings.

计算结果如图2所示，随着燃料球填充率(Packing值)的增加，燃料球间填充的熔盐体积相应减少，从而拉近了燃料球的距离，减少了熔盐对于中子的吸收，整个堆芯的Keff也随之增大，实验计算的最大误差约为0.38%。

图2 2 MW先进高温堆Keff随燃料球体积填充率的变化Fig.2 2 MW AHTR Keff as a function of pebble packings.

2.2堆芯活性区能谱

在对中子能谱进行计算时，我们选取燃料区作为MCNP统计区域。由于体积填充率对于能谱的影响较小，我们选取体积填充率(Packing值)分别为0.5236、0.55、0.605、0.65、0.70及0.7405六组模型，对其能谱进行分析。图3(a)给出的是这六组模型能谱的整体曲线图，为了便于观察，图3(b)给出了能量高于1 eV的中子能谱。

由图3(b)可以看出，随着燃料球体积填充率的增加，中能中子及快中子在整个能谱中所占的份额也相应略有增加，由图3(a)看出，总的中子注量率也略有上升，而热中子所占份额略有下降。原因与Keff变化的理由相同，燃料球间填充的熔盐体积相应减少，从而拉近了燃料球的距离，减缓了燃料球间熔盐的含量，在先进高温堆中，熔盐既是冷却剂也是慢化剂，熔盐减少，相当于减少了慢化剂，使其对中子的慢化效应下降。总的中子注量率及中能中子与快中子所占份额自然也升高。

当然，因为是小功率概念堆，燃料球体积填充率变化引起球间熔盐含量的变化较小，对于能谱的影响也没有那么明显，但是对于以后大型商业化堆的建设，因为燃料球数目较多，燃料球体积填充率的变化引起球间熔盐含量的变化将变大，对于能谱的影响也会增大。而变化的趋势与本文中小功率堆的趋势应该是一致的。

2.3堆芯中子注量率分布

图4给出了中子注量率在空间的分布。计算时，我们选取全堆芯作为MCNP统计区域。由图 4(a)，在燃料总装载量不变的情形下，随着燃料球体积填充率的增加，燃料区的总体积相应减小，中子注量率峰值所在的位置向高处移动。这主要是因为在燃料总装载量无变化的情况下，堆芯活性区的总体积随燃料球体积填充率的增加而减少，而燃料球密度小于熔盐密度，燃料球浮于整个堆芯的上部，活性区的上边界与侧边界位置无法改变。这样，堆芯活性区体积的减少致使活性区下边界上移，下部熔盐区增加，使整个活性区中心上移。那么，中子注量率峰值所在的位置自然会向高处移动。由图4(b)，燃料球体积填充率的变化对于中子注量率峰值在径向的位置影响很小。这主要是因为燃料球与堆芯壁面相切，因此不能通过调节球与壁面间的距离来调节堆芯活性区的大小。

图4 堆芯中子注量率轴向(a)和径向(b)分布受燃料球体积填充率的影响Fig.4 Variation of axial core(a) and radial core(b) neutron flux distribution with pebble packings.

3 结语

(1) 随着燃料球体积填充率的增加，整个堆芯的Keff随之增大。

(2) 燃料球体积填充率的增加，使总的中子注量率有所增加，也使中能中子及快中子在整个能谱中所占的份额相应增加，而热中子所占份额呈现下降趋势。

(3) 燃料球体积填充率的增加，对于中子注量率峰值在轴向所在的位置影响较大，向高处移动。而对于中子注量率峰值在径向所在位置影响很小。

1 秋穗正, 张大林, 苏光辉, 等. 新概念熔盐堆的固有安全性及相关关键问题研究[J]. 原子能科学技术, 2009, 43(增刊): 64–75

QIU Suizheng, ZHANG Dalin, SU Guanghui, et al. Research on inherent safety and relative key issues of a molten salt reactor[J]. Atomic Energy Science and Technology, 2009, 43(Suppl): 64–75

2 Forsberg C W, Pickard P, Peterson P F. Molten-salt-cooled advanced high-temperature reactor for production of hydrogen and electricity[J]. Nuclear Technology, 2003, 144(3): 289–302

3 Ingersoll D T, Forsberg C W, Williams D F, et al. Status of preconceptual design of the advanced high-temperature reactor[R]. USA: Oak Ridge National Laboratory, 2004

4 Fratoni M. Development and applications of methodologies for the neutronic design of the Pebble Bed Advanced High Temperature Reactor (PB-AHTR)[R]. USA: University of California, Berkeley, 2008

5 François-Paul, Fabien Koenig. Preliminary study of the pebble-bed advanced high temperature reactor[R]. USA: University of California, Berkeley, 2006

6 常鸿, 杨永伟, 经荥清, 等. 球床式高温气冷堆初次临界物理计算的蒙特卡罗方法模型分析[J]. 核动力工程, 2005, 26(5): 419–424

CHANG Hong, YANG Yongwei, JING Xingqing, et al. Model analysis of Monte-Carlo method for first criticality physics calculation in pebble bed high temperature gas-cooled reactor[J]. Nuclear Power Engineering, 2005, 26(5): 419–424

7 经荥清, 杨永伟, 许云林. 蒙特卡罗方法用于HTR-10首次临界燃料装料预估的校算[J]. 核动力工程, 2005, 26(1): 28–34

JING Xingqing, YANG Yongwei, XU Yunlin. Application of Monte Carlo method for verification calculation in fuel loading prediction for first criticality of HTR-10[J]. Nuclear Power Engineering, 2005, 26(1): 28–34

8 钟兆鹏, 施工, 胡永明, 等. MCNP 程序在反应堆临界计算中的应用[J]. 核动力工程,2003, 24(1): 8–11

ZHONG Zhaopeng, SHI Gong, HU Yongming, et al. Application of MCNP in the criticality calculation for reactors[J]. Nuclear Power Engineering, 2003, 24(1): 8–11

9 刘时贤, 李晓伟, 吴莘馨. 高温气冷堆堆芯球床流动与温度分布均匀性研究[J]. 工程热物理学报,2012, 33(4): 639–643

LIU Shixian, LI Xiaowei, WU Xinxin. Investigation of the flow and temperature uniformity in the reactor core of HTGR[J]. Journal of Engineering Thermophysics, 2012, 33(4): 639–643

CLCTL329

Physical influence of spherical packing rate on the 2 MW AHTR

LI Xiaoheng1,2CHEN Jingen1ZOU Yang1KANG Xuzhong1CAI Xiangzhou1GUO Wei1MEI Longwei1ZHANG Hongfei2

1(Shanghai Institute of Applied Physics,Chinese Academy of Sciences,Jiading Campus,Shanghai 201800,China)
2(School of Nuclear Science and Technology,Lanzhou University,Lanzhou 730000,China)

Background:With a constant fuel inventory, the pebble packing rate has an important influence on the physical property of AHTR. Purpose: This paper attempts to study the influence of the pebble packing on a 2 MW AHTR. Methods: We used Monte Carlo Code MCNP 5 to study the related parameters, such as Keff, neutron spectrum and neutron flux distribution. In the analysis, we changed the packing from 0.7405 to 0.5236. Results: Results show that the changes of the pebble packing could increase the Keffof the core, make the neutron spectrum harder, and make the neutron flux peak up in axial position. Conclusions: Results provide rational theory for the design of AHTR and the development of computation code.

AHTR, Criticality, Volume packing, Pebble, Neutron spectrum, Neutron flux

TL329

10.11889/j.0253-3219.2013.hjs.36.060604

中国科学院战略性先导科技专项( XDA02010100)资助

李晓恒，男，1985年出生，2013年于兰州大学获硕士学位，研究方向：反应堆物理计算

2012-07-19，

2012-10-12