基于TIGGE资料的地面气温和降水的多模式集成预报

智协飞，季晓东，张璟，张玲，白永清，林春泽

(1.气象灾害教育部重点实验室(南京信息工程大学)，江苏南京210044;2.湖北省气象局气象科技服务中心，湖北武汉430074;3.中国气象局武汉暴雨研究所，湖北武汉430074)

0 引言

近20 a数值预报技术取得了飞速发展，在天气预报中所占比重越来越高，并且由传统的单一确定性预报向集合数值预报方向发展(王太微和陈德辉，2007)。尽管数值预报技术取得了重大进展，但由于模式初始场的不确定性及系统偏差的存在，其预报结果与实况存在一定的差异。且各个模式在动力框架、分辨率、初始场、资料同化技术及物理参数化方案等方面存在差异，从而使得各个模式在模拟能力上存在地理差异，多模式集成技术正是在此基础上合理利用各中心模式预报结果以减小模式系统性偏差的有效途径(杨学胜，2001)。

Krishnamurti et al.(1999)最早提出超级集合预报方法并做了大量的试验对该方法进行检验。研究发现，超级集合预报有效地减小了季节气候预测和天气预报的误差，预报效果远优于单个模式和多模式集 合 平 均 (Krishnamurti et al.，1999，2000a，2000b，2007)。Vijaya Kumar et al.(2003)利用超级集合方法对飓风的路径和强度进行预报试验，发现超级集合预报效果也优于单个模式和多模式集合平均。Ross and Krishnamurti(2005)应用超级集合预报技术，利用6个模式的全球数值预报逐日资料，分别对平均海平面气压、500 hPa高度场、200 hPa和850 hPa风场进行超级集合预报，预报时效为1～5 d，通过大量的试验，发现超级集合预报效果优于最好的单个模式和多模式简单集合平均，并且总体上南半球比北半球预报效果好，春秋两季比冬夏两季预报效果更好。其中，对平均海平面气压的预报效果最好，其次是500 hPa高度场、850 hPa和200 hPa风场。最近，Krishnamurti et al.(2009)基于 TIGGE资料中 UKMO、NCEP、ECMWF、BOM、CMA 五个中心全球模式对中国季风区南海季风爆发时降水、梅雨期降水以及台风登陆强降水进行超级集合预报研究，并且将预报时效从1～3 d扩展到10 d进行讨论，对于4～10 d预报超级集合均方根误差仍然最小。多模式集成方法具有有效改进季节气候预测技巧、提高中短期预报准确率和简便实用等优点，在国际上得到广泛研究与应用(Yun et al.，2003;Cartwright and Krishnamurti，2007;Vijaya Kumar et al.，2007)。

超级集合预报技术在我国的研究与应用尚处于起步阶段。陈丽娟等(2005)借用超级集合思想对我国汛期降水预测的各大单位预报结果进行集成，结果表明集合预报效果较稳定，多数情况下优于单个成员预报。赵声蓉(2006)基于国家气象中心T213模式、德国气象局业务模式和日本气象厅业务模式2 m高温度预报，利用神经网络方法中的BP网络建立了我国600多站的温度集成预报系统;对2004年1—5月的预报试验表明，集成的温度预报结果明显优于3个模式单独的预报结果，达到了一定的预报精度。

TIGGE是全球交互式大集合(THORPEX Interactive Grand Global Ensemble)的简称。目前在中国气象局(CMA)、欧洲中期天气预报中心(ECMWF)和美国国家大气研究中心(NCAR)，TIGGE中心收集了来自全球十多个预报中心的集合预报产品(智协飞和陈雯，2010)。智协飞等(2009)和林春泽等(2009)利用TIGGE资料对北半球及中纬度地区地面气温进行多模式超级集合预报试验，发现超级集合预报方法能有效地改进中短期预报的预报技巧，其预报准确率高于单个模式预报和多模式集合平均的预报准确率，并且滑动训练期超级集合预报技巧明显高于传统的固定训练期超级集合预报技巧(智协飞等，2009;Zhi et al.，2009)。此外，Zhi et al.(2011)还对降水的定量化预报进行了多模式集成预报试验，其预报技巧也高于单个模式的预报技巧。王亚男和智协飞(2012)则利用多模式集成方法做降水的统计降尺度预报，结果发现多模式集成的降尺度预报效果明显优于单中心集合平均预报场的降尺度预报效果。

多模式集成预报技巧优于单个模式的预报，但各个集成方法对不同预报要素的改进效果存在差异。本文主要对2007年夏季北半球中高纬度地区地面气温、中低纬度地区降水的多模式预报资料进行集成试验，并讨论了2008年初中国南方极端雨雪冰冻过程的多模式集成预报技巧，期望对多模式集成技术在地面气温和降水预报中的性能进行较全面的评估和试验。

1 资料与方法

1.1 资料

所用资料取自TIGGE资料集下中国气象局(CMA)、欧洲中期天气预报中心(ECMWF)、日本气象厅(JMA)、美国国家环境预报中心(NCEP)和英国气象局(UKMO)5个中心全球集合预报模式每天12时(世界时)起报的地面温度、24 h累积降水的各自集合成员平均。资料时间长度为2007年6月1日—8月31日及2008年1月1日—2月1日，预报时效为24～216 h，间隔24 h。并采用NCEP/NCAR再分析资料和TRMM 24 h累积降水作为“观测值”来进行多模式集成预报和检验预报效果。

1.2 方法

主要采用多模式集合平均(ensemble mean，EMN)、滑动训练期消除偏差(running training period bias-removed ensemble mean，R-BREM)、滑动训练期超级集合(running training period multi-model superensemble，R-SUP)等方法来进行集成预报试验。

多模式集合平均的计算公式为

其中:Fi为第i个模式的预报值;n为参与集合的模式总数。

消除偏差集合平均的计算公式为

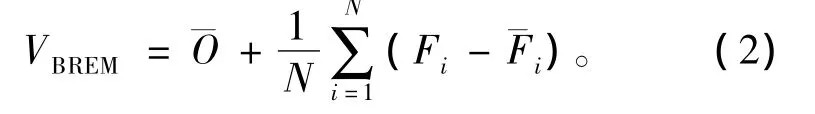
其中:VBREM为消除偏差集合预报值;Fi为第i个模式的预报值;¯Fi为第i个模式预报值在训练期的平均;¯O为观测值在训练期的平均;N为参与集合的模式数。

多模式超级集合是一项统计技术，通过一段时间的模式预报和观测(分析)数据进行训练建模，确定参与集成的模式权重系数，在预报期进行超级集合预报。超级集合预报的建模既可以采用多元回归技术也可以采用非线性神经网络技术。

超级集合预报模型由方程(3)构建，在一个给定的格点上，对于某一预报时效某一气象要素:

式中:St为超级集合预报值;O为训练期观测值平均;Fi，t为第i个模式的预报值;Fi为第i个模式在训练期的预报值平均;ai为回归系数(权重);n为参与超级集合的模式总数;t为时间。

在训练期，回归系数ai由(4)式中的误差项G最小化计算而得(Krishnamurti et al.，2000a):

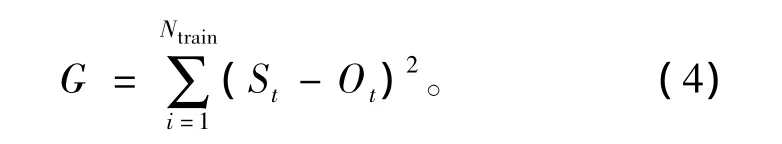
式中:Ot为观测值;Ntrain为训练期时间样本总数。在预报期，将在训练期得到的ai代入到(3)式中，对其他格点也做同样的计算，即可进行超级集合预报。

林春泽等(2009)研究指出，当训练期窗口固定时，超级集合与消除偏差集合平均两种方法对24 h、48 h预报改善的效果相当，在预报期前期，超级集合预报的均方根误差小于消除偏差集合平均的误差，但在后期，超级集合预报的均方根误差超过消除偏差集合平均的误差。对于72～168 h预报，预报期前两周超级集合预报的均方根误差和消除偏差集合平均的均方根误差相当，两周后超级集合预报的均方根误差增长很快，超过了消除偏差集合平均的均方根误差。这主要是因为固定训练期的超级集合预报没有考虑到预报时间远离训练期时，在训练期得到的各模式的权重系数有可能失效，导致预报期后期预报误差出现增长的趋势。为此，本文采用滑动训练期超级集合预报方法，即将固定长度的训练期逐日向后滑动，每次只对距离训练期临近的一天进行预报，这样每天的预报都由新的训练期消除预报偏差，训练新的权重，使预报效果更加稳定。此外，超级集合预报中各模式的权重系数的计算既可以用线性回归方法(林春泽等，2009;智协飞等，2009)，也可用人工神经网络的方法(Geman et al.，1992;Warner and Misra，1996)来确定。本文基于神经网络的超级集合预报采用的是3层BP神经网络结构，网络包括1个隐层，隐层节点数为4个，输入节点数为4个，分别为ECMWF、JMA、NCEP和UKMO中心的集合平均结果(白永清，2010;Zhi et al.，2012)。

2 地面气温的多模式集成预报试验

图1 2007 年8 月8—31 日每天24 h(a)、48 h(b)、72 h(c)、96 h(d)、120 h(e)、144 h(f)和168 h(g)地面温度预报的北半球0°～357.5°E、10～87.5°N区域的平均均方根误差(单位:℃)Fig.1 Mean root-mean-square errors(RMSEs)of surface air temperature forecasts for(a)24 h，(b)48 h，(c)72 h，(d)96 h，(e)120 h，(f)144 h and(g)168 h averaged over the land area of(10—87.5°N，0°—357.5°E)from 8 to 31 August 2007(units:℃)

图1给出2007年8月8—31日预报期24～168 h时效的简单集合平均(EMN)、线性回归超级集合(LRSUP)、神经网络超级集合(NNSUP)以及滑动训练期线性回归超级集合(R-LRSUP)、滑动训练期神经网络超级集合(R-NNSUP)预报在北半球区域的平均均方根误差。可见，改进后的滑动训练期的超级集合在整个预报期内效果稳定，预报后期误差没有再出现明显的增长趋势，预报后期效果得到改善。尤其对于预报时效较长的，滑动训练期的超级集合使得整个预报期内误差均低于EMN，从而进一步改善了预报效果。其中R-NNSUP预报效果要比R-LRSUP更好一些。此外，对北半球各纬度带预报效果进行对比分析发现，滑动训练期超级集合(RSUP)预报方法对低纬度地区的预报改善效果最为显著，中纬度地区次之，且在中低纬度地区预报效果均明显优于最优单个中心，而对于高纬度地区的预报改善效果并不明显(白永清，2010)。

3 北半球中低纬度降水的多模式集成试验

R-SUP试验对地面温度预报是成功的，尤其对于中低纬度地区，超级集合预报效果要远好于单模式预报及它们的集合平均。而对于24 h累积降水，超级集合预报效果不很理想，预报误差甚至超过单模式预报。这可能是因为降雨的发生是不连续的，降雨量大小的波动会造成训练期内样本距平的急剧波动。由多元线性回归方法或者神经网络方法在训练期确定权重时，过度拟合了某几个样本距平的极大值，这种过拟合现象使得各模式的回归系数发生了扭曲，以至于权重不能真实地反映整个训练期模式的预报能力，这可能是造成降水超级集合预报效果不理想的一个原因。此外，由于各模式的降水量预报不稳定，预报误差变化幅度很大，因此在预报期内各个模式的预报结果很难遵从训练期内模式权重的规律。前人在做降水的超级集合试验中，通过使用大量样本来训练一组较为稳定的权重系数，充足的样本包含了各类降雨事件，训练期一般选用120～150 d甚至更长。而本文只有88 d样本序列，各类降雨样本也不充足，未能训练出稳定的权重系数，这可能也是造成超级集合效果不理想的另一原因。基于以上分析，选用BREM方法对北半球中低纬度地区的24 h累积降水进行回报试验。

利用5个集合预报中心2007年6月1日—8月27日88个样本，对北半球中低纬度地区1.25～358.75°E、10 ～48.75°N 进行各时效 24 h 累积降水集合预报试验。为了充分利用样本，选用交叉检验的思想，即从试验资料序列的第一个样本开始，每次轮流留出一个样本，用余下的样本建立预报方程，并对留出的样本作回报试验(Yun et al.，2003)。这样依次进行，直到全部样本都做完独立的回报试验。

图2给出了2007年6月1日—8月27日北半球中低纬度地区各中心预报结果、集成预报结果与“实况场”TRMM结果的距平相关系数，其中5个中心模式预报结果与“实况场”逐日距平相关系数用浅色细线表示，EMN和BREM分别用深色粗线表示。可以看到，对于24～168 h预报，在所有样本中多模式集成的结果均好于单个模式的结果，且集成结果相对任何一个中心的模式都要稳定，其中BREM略好于EMN。对24 h预报时效的降水，各中心模式的相关系数均在0.6以下，集成后的相关平均达到0.6以上。均方根误差(RMSE)的检验结果(图略)与距平相关系数的检验结果一致，与单个中心模式结果相比，多模式集成的结果均方根误差最小，且BREM的误差略低于EMN的结果。

通过距平相关分析和均方根检验，从总体上检验各个中心及集成结果对北半球中低纬度地区24 h累积降水的预报能力，下面进一步分析各中心对降水场分布的预报能力及多模式集成方法对降水场的改进情况。

图3给出了2007年6月1日—8月27日24 h预报时效平均降水场的分布情况，并对各个中心及多模式集成的结果进行了均方根误差和距平相关系数的分析。从TRMM资料降水分布可见，2007年夏季亚洲至太平洋西部、北美洲至大西洋西部平均有1 mm以上降水，其中印度、孟加拉湾、亚洲东部局部地区以及沿赤道太平洋东部有较强的降水。此外，ECMWF预报误差最小，为1.77 mm/d，JMA预报误差最大，为2.99 mm/d;而UKMO预报的距平相关系数最高，达0.87，CMA预报的最低，为0.73。ECMWF与CMA对印度西部及孟加拉湾地区的强降水中心预报偏弱，整体而言，各中心对降水量的预报普遍偏强。与单个中心的结果相比，多模式集成的结果更为理想，EMN预报误差为2.01 mm/d，相关系数达到0.89，BREM的结果与“实况场”最为接近，其均方根误差降低至0.69 mm/d，距平相关系数高达0.98。

4 极端事件的多模式集成试验

2008年1月10 日至2月2日，受冷暖空气共同影响，中国南方出现4次明显的雨雪天气过程，南方大部地区遭受了历史罕见的低温、雨雪、冰冻灾害(Wen et al.，2009)，其中1/3以上地区出现了50 a一遇的多雨雪天气(Zhang and Zhi，2009)。持续的灾害性天气过程，给人民生产和生活造成了严重的影响和损失。提高预报准确率、延长预报时效将有利于预报持续性的灾害性天气过程，提高防灾、抗灾的能力。本文针对此次灾害性过程，进一步讨论多模式集成预报方法对极端事件预报能力的改进情况。

综合2007年夏季的试验结果，R-SUP预报方法对连续性要素的改进效果显著，而对于降水，R-SUP预报的结果并不理想，BREM的改进效果较好。但传统的BREM方法需要较长时间的训练期进行消除偏差处理以达到稳定结果的目的，这就对资料的时间长度和计算能力提出较高的要求。在本次试验中，利用滑动训练期的思想，采用R-BREM方法对此次过程的地面气温和24 h累积降水进行多模式集成试验，以检验较短训练期多模式集成方法对预报的改进能力。

4.1 地面气温预报

图2 2007年6月1日—8月27日北半球中低纬度区域(1.25～358.75°E、10～48.75°N)的24 h(a)、48 h(b)、72 h(c)、96 h(d)、120 h(e)、144 h(f)和168 h(g)的24 h累积降水预报与 TRMM 资料的距平相关系数Fig.2 Anomaly correlation coefficients between TRMM data and 24 h accumulated precipitation forecasts for(a)24 h，(b)48 h，(c)72 h，(d)96 h，(e)120 h，(f)144 h and(g)168 h averaged over the area(10—48.75°N，1.25—358.75°E)from 1 June to 27 August 2007

首先对温度场进行多模式集成预报试验，基于ECMWF、JMA、NCEP、CMA 四个数值中心 2008 年1月1—31日地面气温预报(预报时效为24～216 h，间隔24 h)，选取6 d为训练期，各预报时效均以1月16—31日共16 d作为预报期，以同期的NCEP/NCAR再分析资料作为“观测值”，进行多模式集成预报试验。

图4 给出了 JMA、ECMWF、NCEP、CMA、EMN、BREM、R-BREM 2008年1月16—31日中国南方地面气温预报的区域平均均方根误差，预报时效为24～216 h，时效间隔为24 h。可以看出，在4个中心的预报结果中，CMA的预报结果相对较差，ECMWF的预报结果相对较好。选取模式预报能力相对较好的3个中心(JMA、ECMWF、NCEP)的预报资料进行多模式集成对比试验。在预报期，EMN的均方根误差略低于3个中心的单个误差，RBREM预报的误差最小，改进效果最好。

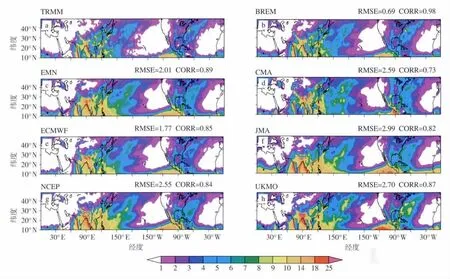
图3 2007年6月2日—8月28日“实况场”TRMM的气候平均日降水量(a;单位:mm)和各个中心的24 h预报的同时段平均日降水量及其多模式集成预报结果的比较(b—h;RMSE表示日降水量24 h预报的均方根误差，单位:mm;CORR表示24 h预报和TRMM资料的距平相关系数)Fig.3 The intercomparison of mean 24 h accumulated precipitation among(a)TRMM data and(b—h)24 h forecasts for different single models including CMA，ECMWF，JMA，NCEP and UKMO and their multimodel ensemble forecasts from 2 June to 28 August 2007(RMSE represents root-mean-square error of 24 h accumulated precipitation forecast with the unit of mm，while CORR represents the anomaly correlation coefficients between 24 h precipitation forecast and TRMM data)

图4 2008年1月16—31日中国南方地面气温平均均方根误差(单位:℃)Fig.4 RMSEs of 24—216 h forecasts of surface air temperature averaged over southern China from 16 to 31 January 2008(units:℃)

为了检验多模式集成预报方法对预报时效改进的情况，选取1月25日—2月1日两次雨雪降温过程，分析单个数值预报中心、EMN、R-BREM 在不同预报时效对这两次降温过程的预报误差。为了更加直观地展现多模式集成预报方法对预报时效的改进效果，选取预报效果较好的ECMWF提前96 h对1月25日—2月1日预报的均方根误差，以此误差为基准，比较EMN、R-BREM预报结果达到此误差时能够延长的预报时效。如图5所示，EMN并没能改善对中国南方大部分地区的预报效果，R-BREM将中国南方大部分地区的预报时效延长了96 h，使得预报时效延伸至192 h，但对贵州西部的预报效果不如ECMWF。对于中国南方大部分区域，R-BREM有效降低了预报的均方根误差，延长了预报时效。

4.2 降水预报

图5 2008年1月25日—2月1日地面气温的EMN(a)和R-BREM(b)预报相对于ECMWF 96 h预报的预报时效延长时间(单位:h)Fig.5 The prolonged forecast lead time of(a)EMN and(b)R-BREM forecasts of surface air temperature against ECMWF 96 h forecast from 25 January to 1 February 2008(units:h)

基于 CMA、JMA、ECMWF、NCEP 四个中心2008年1月1—31日24 h累积降水预报(预报时效为24～216 h，间隔24 h)，选取6 d为训练期，各预报时效均以1月16—31日共16 d作为预报期，以同期的TRMM(Tropical Rainfall Measuring Mission)资料作为“观测值”，进行多模式集成试验。图6给出了2008年1月16—31日CMA、JMA、ECMWF、NCEP、EMN、R-BREM 24 h累积降水 144 h 预报，在预报期16 d的平均均方根误差地理分布。可见，CMA(图6a)在中国南方144 h时效的24 h累积降水的均方根误差普遍超过4 mm，误差的大中心区域出现在广西东部和广东西部，误差超过21 mm，江南、华南地区的误差均超过10 mm。对比JMA(图6b)、ECMWF(图 6c)、NCEP(图 6d)的预报结果可以发现，误差的大值中心与CMA的结果一致，均位于两广的交界处，且中心误差超过21 mm，但各中心的预报误差在华东和华中地区存在一定差异。由于各单个中心在此试验期间的误差分布不存在较为显著的地理差异，因此多模式集成(图6e、f)的改进效果并不显著，对误差大值中心的改进效果极差，但对于中国南方大部分区域的预报结果还是有一定的改进，尤其是对安徽南部、浙江西部、江西北部的改进效果较为明显。R-BREM方法对预报结果的改进程度要大于EMN的。

为了检验多模式集成预报方法对预报时效改进的情况，选取1月25日—2月1日两次雨雪降温过程，比较单个数值预报中心、EMN、R-BREM在不同时效对这两次雨雪过程的预报误差。分别对CMA、JMA、ECMWF、NCEP、EMN 和 R-BREM 的预报结果进行了分级TS评分。图7给出了CMA、JMA、ECMWF、NCEP、EMN和R-BREM 在不同预报时效对1月25日—2月1日中国南方24 h累积降水各降水量级的TS评分。比较四个数值中心对中国南方小雨(0.1～10 mm/(24 h))的预报结果，除24 h外，其他时效JMA的预报结果均好于其他预报中心。随着降水量级的增加，各个数值中心的评分显著下降。对于中国南方中雨的预报(10～25 mm/(24 h))JMA的预报评分波动较大，ECMWF的预报结果相对稳定，CMA的预报技巧相对较低。选用预报能力相对较好的三个中心(JMA、ECMWF、NCEP)的预报结果进行多模式集成试验，对于小雨的预报除72 h、216 h外，大部分时效滑动训练期消除偏差集合平均的预报结果优于单个中心的结果，提高了降水的TS评分。而对于中雨的预报滑动训练期消除偏差集合平均从24 h至192 h预报结果的TS评分均高于单个数值中心的预报结果。

5 结论与讨论

基于TIGGE资料集下 CMA、JMA、ECMWF、NCEP、UKMO五个中心的集合预报结果，对北半球中高纬度地区的地面气温、中低纬度地区24 h累积降水以及2008年初中国南方极端雨雪冰冻过程进行多模式集成试验，进一步讨论各种多模式集成方法的适用性，得到以下几点结论:

1)对于地面气温预报，滑动训练期超级集合预报方法明显优于其他多模式集成方法，其预报误差最小，且在较长预报期内预报结果保持稳定。基于神经网络的滑动训练期超级集合预报效果略优于基于线性回归的滑动训练期超级集合预报。

2)对于24 h累积降水预报，超级集合的效果不甚理想，误差甚至超过单个模式结果。但无论是以均方根误差还是以距平相关系数来评价模式的预报效果，消除偏差集合平均结果均好于单个中心预报。

3)对于2008年初中国南方低温雨雪冰冻灾害的预报，滑动训练期消除偏差集合平均方法最优。对于地面气温的预报在固定误差范围内，该方法能将大部分地区的预报时效由最优数值预报中心的96 h延长至192 h，有利于提高持续异常天气过程预报的准确率。对于24 h累积降水的预报，除个别预报时效外，滑动训练期消除偏差集合平均方法有效地提高了小雨、中雨的TS评分。

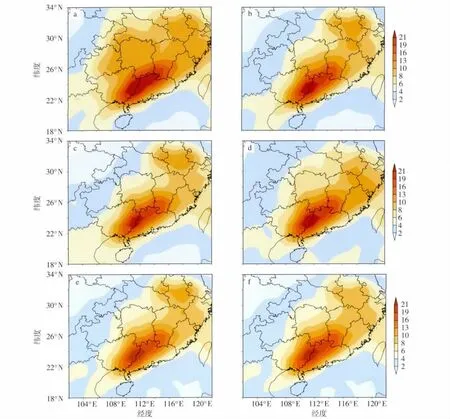
图6 2008年1月16—31 日 CMA(a)、JMA(b)、ECMWF(c)、NCEP(d)、EMN(e)、R-BREM(f)24 h累积降水144 h预报平均均方根误差的地理分布(单位:mm)Fig.6 The geographical distributions of mean RMSEs of 24 h accumulated precipitation forecasts with forecast time of 144 h for(a)CMA，(b)JMA，(c)ECMWF，(d)NCEP，(e)EMN and(f)R-BREM from 16 to 31 January 2008(units:mm)

训练期长度的选择对预报效果的影响较为显著，在使用滑动训练期多模式集成方法时，应根据预报要素的特征选择最优训练期以获得最佳的预报效果。

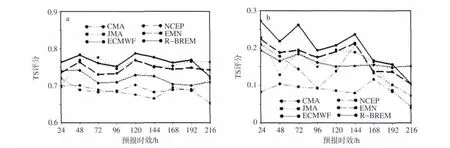
图7 不同预报时效对1月25日—2月1日中国南方24 h累积降水的小雨(a)、中雨(b)的TS评分Fig.7 TS scores of(a)light and(b)moderate rains for 24 h accumulated precipitation with different forecast times from 24 h to 216 h over southern China from 25 January to 1 February 2008

白永清.2010.基于TIGGE资料多模式地面要素的超级集合预报［D］.南京:南京信息工程大学.

陈丽娟，许力，王永光.2005.超级集合思想在汛期降水预测集成中的应用［J］.气象，31(5):52-54.

林春泽，智协飞，韩艳，等.2009.基于TIGGE资料的地面气温多模式超级集合预报［J］.应用气象学报，20(6):706-712.

王太微，陈德辉.2007.数值预报发展的新方向——集合数值预报［J］.气象研究与应用，28(1):6-12.

王亚男，智协飞.2012.多模式降水集合预报的统计降尺度研究［J］.暴雨灾害，31(1):1-7

杨学胜.2001.业务集合预报系统的现状及展望［J］.气象，27(6):3-9.

赵声蓉.2006.多模式温度集成预报［J］.应用气象学报，17(1):52-58.

智协飞，陈雯.2010.THORPEX国际科学研究新进展［J］.大气科学学报，33(4):504-508.

智协飞，林春泽，白永清，等.2009.北半球中纬度地区地面气温的超级集合预报［J］.气象科学，29(5):569-574.

Cartwright T J，Krishnamurti T N.2007.Warm season mesoscale superensemble precipitation forecasts in the southeastern United States［J］.Wea Forecasting，22:873-886.

Geman S，Biensenstock E，Doursat R.1992.Neural networks and the bias/variance dilemma［J］.Neural Computation，4:1-58.

Krishnamurti T N，Kishtawal C M，LaRow T E，et al.1999.Improved weather and seasonal climate forecasts from multimodel superensemble［J］.Science，285:1548-1550.

Krishnamurti T N，Kishtawal C M，Zhang Z，et al.2000a.Multimodel ensemble forecasts for weather and seasonal climate［J］.J Climate，13:4197-4216.

Krishnamurti T N，Kishtawal C M，Shin D W，et al.2000b.Improving tropical precipitation forecasts from multianalysis superensemble［J］.J Climate，13:4217-4227.

Krishnamurti T N，Gnanaseelan C，Chakraborty A.2007.Prediction of the diurnal change using a multimodel superensemble.Part I:Precipitation［J］.Mon Wea Rev，135:3613-3632.

Krishnamurti T N，Sagadevan A D，Chakraborty A，et al.2009.Improving multimodel forecast of monsoon rain over China using FSU superensemble［J］.Adv Atmos Sci，26(5):819-839.

Ross R S，Krishnamurti T N.2005.Reduction of forecast error for global numerical weather prediction by the Florida State University Superensemble［J］.Meteor Atmos Phys，88:215-235.

Vijaya Kumar T S V，Krishnamurti T N，Fiorino M，et al.2003.Multimodel superensemble forecasting of tropical cyclones in the Pacific［J］.Mon Wea Rev，131:574-583.

Vijaya Kumar T S V，Sanjay J，Basu B K，et al.2007.Experimental superensemble forecasts of tropical cyclones over the Bay of Bengal［J］.Natural Hazards，41:471-485.

Warner B，Misra M.1996.Understanding neural networks as statistical tools［J］.Amer Stat，50:284-293.

Wen M，Yang S，Kumar A，et al.2009.An analysis of the large-scale climate anomalies associated with the snowstorms affecting China in January 2008［J］.Mon Wea Rev，137:1111-1131.

Yun W T，Stefanova L，Krishnamurti T N.2003.Improvement of the multimodel superensemble technique for seasonal forecasts［J］.J Climate，16:3834-3840.

Zhang Ling，Zhi Xiefei.2009.The features and possible causes of the extreme event with freezing rain and snow over the southern China in early 2008［C］//Abstracts，Climate change and tropical climatic hazards in Asia Oceania，6th Annual Meeting of Asia Oceania Geosciences Society.Singapore:Asia Oceania Geosciences Society.

Zhi Xiefei，Bai Yongqing，Lin Chunze，et al.2009.Multimodel superensemble forecasts of the surface air temperature in the Northern Hemisphere［C］//Abstract，Third THORPEX International Science Symposium.California，USA:WMO:57.

Zhi Xiefei，Zhang Ling，Bai Yongqing.2011.Application of the Multimodel Ensemble Forecast in the QPF［C］//Proceedings of International Conference on Information Science and Technology.Nanjing，China:IEEE:657-660.doi:10.1109/ICIST.2011.5765333.

Zhi Xiefei，Qi Haixia，Bai Yongqing，et al.2012.A comparison of three kinds of multimodel ensemble forecast techniques based on the TIGGE data［J］.Acta Meteor Sinica，26(1):41-51.doi:10.1007/s13351-012-0104-5.