热带气旋复杂程度的分形维数表征

邵丽芳，罗哲贤，马革兰，滕代高，王新伟，倪东鸿

(1.气象灾害教育部重点实验室(南京信息工程大学)，江苏南京210044;2.南京信息工程大学大气科学学院，江苏南京210044;3.南京信息工程大学环境科学和工程学院，江苏南京210044;4.浙江省气象台，浙江杭州310017;5.南京信息工程大学 遥感学院，江苏 南京210044)

0 引言

热带气旋(TC)在当今十大急性自然灾害中造成的死亡人数最多。我国位处西太平洋沿岸，TC灾害居于亚洲诸国之首。要减轻TC灾害，首先要给出TC移动路径的正确预报。

环境场引导气流(Chan and Gray，1982;Carr and Elsberry，1998;周伟灿和王灿伟，2009;苏源和吴立广，2011;赵大军等，2011)、TC环流的非对称结构(Fiorino and Elsberry，1989;田永祥，1994;林毅，1997;田永祥等，2000)和非对称对流系统(马镜娴等，1995;Chen and Luo，1995)被认为是影响 TC路径的三个基本因子(Elsberry，1995)。近半个多世纪以来，TC移动动力学的工作一般针对单个基本因子的作用开展研究，属于单因子的工作框架(罗哲贤和平凡，2012)。

Elsberry(2007)近来指出了单个基本因子工作框架的缺陷，并认为TC路径预报的问题比单个基本因子的理想框架要困难得多。关键是，TC路径预测是一个复杂的非线性问题。我们认为，Elsberry提出了TC移动动力学研究的新思路。既然TC路径预测是一个复杂的非线性问题，这就需要把TC路径预测和非线性理论结合起来。一般认为，非线性理论包含混沌理论、分支理论、分形理论和自组织理论等。另一方面，除了TC环流的非对称结构以外，复杂结构对TC路径的影响也受到关注(Luo et al.，2011)。

本研究将应用非线性理论中的分形理论，用TC边缘线的分形维数定量表征TC环流的复杂结构。用此途径，把TC路径预测问题和非线性理论初步结合起来。后续的研究将分析TC边缘线的分形维数，以及TC环流的复杂结构和TC异常路径的联系。这些工作是用Elsberry新思路开展的探索性研究，在TC路径预报方面有应用前景。

1 资料与方法

1.1 资料

1)从2006—2009年的热带气旋年鉴以及2010年台风云系降水对我国造成影响的热带气旋中选出69个，分别为 0513(泰利)、0514(彩蝶)、0515(卡努)、0516(韦森特)、0518(达维)、0519(龙王)、0521(启德)、0601(珍珠)、0602(杰拉华)、0603(艾云尼)、0604(碧利斯)、0605(格美)、0606(派比安)、0608(桑美)、0609(宝霞)、0613(珊珊)、0615(未命名)、0616(象神)、0617(贝碧嘉)、0621(飞燕)、0622(榴莲)、0623(尤特)、0703(桃芝)、0704(万宜)、0707(帕布)、0708(蝴蝶)、0709(圣帕)、0712(百合)、0713(韦帕)、0714(范斯高)、0715(利奇马)、0716(罗莎)、0722(琵琶)、0724(米娜)、0725(海贝思)、0801(浣熊)、0806(风神)、0807(海鸥)、0808(凤凰)、0809(北冕)、0812(鹦鹉)、0813(鹦鹉)、0814(黑格比)、0815(蔷薇)、0816(米克拉)、0817(海高斯)、0902(灿鸿)、0903(莲花)、0904(浪卡)、0905(苏迪罗)、0906(莫拉菲)、0907(天鹅)、0908(莫拉克)、0913(彩虹)、0915(巨爵)、0916(凯萨娜)、0917(芭玛)、0918(茉莉)、0920(卢碧)、0921(银河)、1002(康森)、1003(灿都)、1005(蒲公英)、1006(狮子山)、1007(圆规)、1008(南川)、1010(莫兰蒂)、1011(凡亚比)、1013(鲇鱼)。从这69个TC资料中，提取了1 295个时次的Black Body Temperature(缩写为TBB)，即红外亮温资料。

2)上海台风所提供的2006—2009年台风生命史中地球静止卫星高分辨红外亮温资料(TBB)。该资料是以台风为中心、12个经纬距为半径的矩形区域，空间分辨率为0.05°×0.05°，时间分辨率为1 h(表1)。

3)2010年的MTSAT卫星的红外云图资料及对应的灰度转换数据，该资料从日本高知大学的气象网 站 (http://weather.is.kochi-u.ac.jp/sat/G/AME/)获得。MTSAT红外云图卫星资料空间范围为70 ～160°E、70°N ～20°S，空间分辨率为 0.05°×0.05°，时间分辨率为1 h，存储格式为PGM格式，灰度转换表数据为文本格式(表1)。

4)中国气象局(CMA)1949—2010年TC最佳路径资料，从中国台风网(http://www.typhoon.gov.cn/data/detail.php?id=33＆type=5＆style=)下载，分年存储为txt文本格式。具体的资料格式详见网站上的格式说明文件《CMA-STI最佳路径数据格式说明.pdf》。

表1 TBB和红外云图资料的属性Table 1 Attributes of TBB data and IR images

1.2 方法

1.2.1 TC外缘线的提取

首先下载2010年9个TC(TC编号分别为1002、1003、1005、1006、1007、1008、1010、1011 和1013)生命史中每6 h一次的红外云图资料，资料为PGM格式(表1)。根据CMA提供的台风中心位置数据，读取这9个TC每6 h一次的TC中心位置。以TC中心为中心，以12个经纬距为半径，截取红外云图资料，截取范围与上海台风所提供的资料范围一致，并且根据灰度转换表转换成对应的TBB数据，格式同上海台风所提供的资料(表1)。最后绘制－32℃的TBB等值线，并从所有等值线中提出台风的－32℃闭合TBB等值线，以此作为TC外缘线。Maddox(1980)认为TBB值大于－32℃存在着非对流云或很弱的对流，把－32℃作为有无对流发展的阈值。TC云系主要由对流云系组成，因此选用－32℃等值线作为TC外缘线。图1给出了提取TC外缘线的一个例子。

1.2.2 分形维数的计算

分形维数又称分维或分维数，是描述分形集的自相似程度、不规则程度或破碎程度的定量参数。分形维数提供了一种描述自然界和非线性系统中不光滑和不规则几何体不规则程度(或者说复杂度、粗糙程度)的客观工具。目前常用的计算分维数的方法有:改变观察尺度求维数，根据测度关系求维数，根据密度函数求维数，利用分布函数求维数，频谱法等。本文选用改变观察尺度求维数的圆规法。圆规法(张济忠，1995;曾文曲和王向阳，2001)介绍如下:

设C是分形曲线，则

式中:LE表示C的欧式长度;LH表示C的Hausdorff长度;δ表示C的标度;D是C的分形维数。如果δ为圆规间距，则LE可看作是间距为δ的圆规测量C所得的长度，LE/δ则为以δ为步长，测量C时所得的步数。记作:

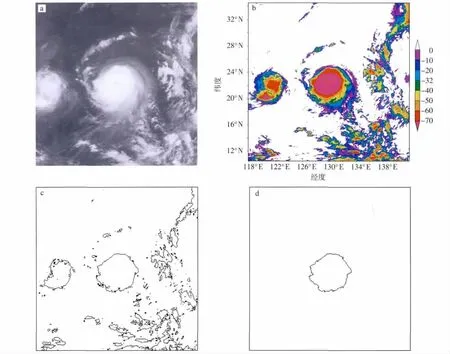
图1 提取热带气旋边缘线步骤 a.红外云图;b.TBB图(单位:℃);c.－32℃的TBB等值线;d.热带气旋边缘线Fig.1 The steps of extracting TC edge a.IR image;b.TBB image(units:℃);c.TBB contour of －32 ℃;d.TC edge

这里D就是圆规法计算出来的分形维数。在不同的步长δi(标度)下，测量分形曲线C得到不同的Ni(δi);在双对数坐标中，拟合数据 (－ ln δi，ln Ni(δi))所得直线斜率即为D的估计值。

1.2.3 分形维数圆规法计算机实现及验证

1)圆规法计算机实现

a.选定步长k=1;

b.以第一点i=1作为起点，j=i+1下一点作为终点;

c.计算起点与终点间的距离d;

d.如果d＜k，将j=j+1作为终点，计算d;

e.如果d=k，步数N(k)加1，将j点作为起点，将j=j+1作为终点，重复步骤c到f;

f.如果 d＞k，步数 N(k)加1，利用三角函数，在j和j－1两点连线上找到d=k的点，作为起点，j为终点;重复步骤c到f，直到最后一个点;

g.步长 k=k+1，重复步骤 b到 f，直到最大步长;

h.对所有的步长 k，计算 －ln k，步数 N(k)，计算ln N(k)，绘制散点图。

2)验证

利用上述程序计算圆和Koch曲线的分形维数。Koch曲线是一个数学曲线，是早期被描述的一种分形曲线。它由瑞典数学家Helge von Koch在1904年提出，其理论分形维数是lg4/lg3≈1.26(陈颙和陈凌，2005)。利用本文算法计算出圆的维数为1.001 7，Koch曲线的分形维数为1.264 2，二者与理论维数的绝对误差分别为0.001 7和0.002 2，相对误差均为0.17%(表2)。由表2可见，计算值与理论值是接近的。

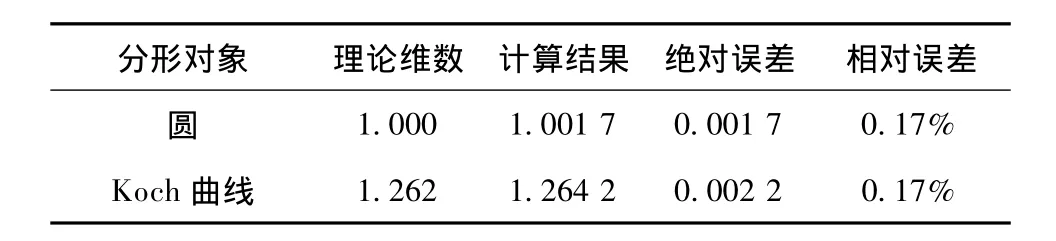
表2 圆和Koch曲线的分形维数Table 2 Fractal dimension of circle and Koch line

2 主要结果

本文选取1 295个TC边缘线样本，对每个样本计算了分形维数。得到了1 295个分形维数。将这1 295个数自小到大排列，按等频数规则，将1 295个数分为 5类，分别记为 A、B、C、D、E类。A、B、C、D、E 类分形维数的均值分别为 1.21、1.26、1.29、1.33、1.40。然后寻找与这5个均值最接近的样本。结果是:2006年8月5日00时0907号台风，分形维数为1.21;2009年6月24日07时0904号台风，分形维数为1.26;2007年8月17日00时0709号台风，分形维数为1.29;2007年9月18日18时0713号台风，分形维数为1.33;2006年9月28日12时0616号台风，分形维数为1.40。

这5个样本的红外云图和TBB等值线分别如图2—6所示。可见:1)随着分形维数的加大，边缘线的非光滑程度逐渐加大;2)图形与准圆形的偏离程度逐渐加大，TC空间结构的复杂程度也逐渐加大。说明:外缘线的分形维数可以在一定程度上定量表征TC的复杂程度。

图2 2006年8月5日00时0606号TC的红外云图(a)和－32℃的TBB等值线(b)Fig.2 (a)Infrared image and(b)TBB contour of －32℃ for TC 0606 at 0000 UTC 5 August 2006

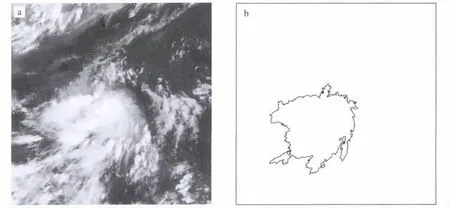
图3 2009年6月24日07时0904号TC的红外云图(a)和－32℃的TBB等值线(b)Fig.3 (a)Infrared image and(b)TBB contour of －32℃ for TC 0904 at 0700 UTC 24 June 2009

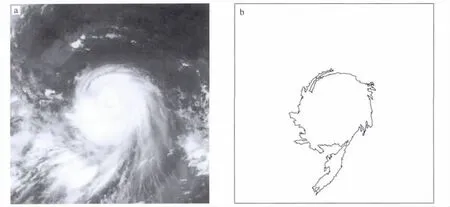
图4 2007年8月17日00时0709号TC的红外云图(a)和－32℃的TBB等值线(b)Fig.4 (a)Infrared image and(b)TBB contour of －32℃ for TC 0709 at 0000 UTC 17 August 2007

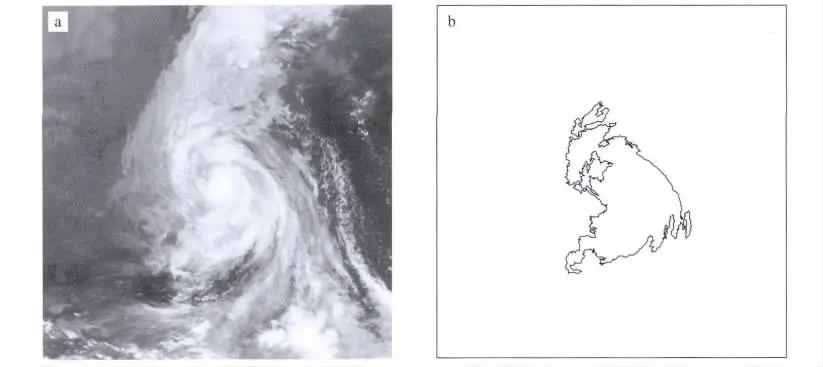
图5 2007年9月18日18时0713号TC的红外云图(a)和－32℃的TBB等值线(b)Fig.5 (a)Infrared image and(b)TBB contour of －32℃ for TC 0713 at 1800 UTC 18 September 2007

3 结论

图6 2006年9月28日12时0616号TC的红外云图(a)和－32℃的TBB等值线(b)Fig.6 (a)Infrared image and(b)TBB contour of －32℃ for TC 0616 at 1200 UTC 28 September 2006

首先，本文提出了一个定量描述TC复杂结构的方法。应用TC红外云图和TBB资料，提取TC环流的外缘线。计算外缘线的分形维数。该分形维数在一定程度上可以表征TC结构的复杂程度。其次，用1 295个TC环流外缘线的资料，计算得到1 295个分形维数。再用等频数分类的方法，将1 295个数自小到大分为5级，并求出各级的平均值。再次，从1 295个分形维数中识别出最接近各级平均值的5个值，确定这5个值相应的时间，包括年、月、日、时。对比这5个时间TC红外云图和TBB分布可见，随着分形维数的增加，TC的结构也趋于复杂。

如所知，TC和相邻中尺度对流系统的作用是一个三维空间的问题，但是，注意到三维对流系统在对流层中层往往对应一个中尺度涡，因此，有些研究，如Enagonio and Montgomery(2001)和Chen and Luo(2006)，把TC和相邻中尺度对流系统作用的三维问题，简化为TC和中尺度涡作用的二维问题。类似地，TC的结构是一个三维问题，但是，目前红外云图等反映的一般是二维空间的特征，在此基础上，只能在二维平面的框架内分析TC环流复杂结构的表征问题。今后应该继续研究TC三维复杂结构的表征问题。

陈颙，陈凌.2005.分形几何［M］.北京:地震出版社:82-86.

林毅.1997.9608台风内区云系结构演变与路径变化［J］.气象科学，17(4):350-357.

罗哲贤，平凡.2012.眉状中尺度涡影响热带气旋路径的机理研究［J］.中国科学:地球科学，42(2):290-300.

马镜娴，刘晓东，李茜，等.1995.较小尺度涡旋与台风的相互作用及其对台风路径的影响［J］.南京气象学院学报，18(2):187-191.

苏源，吴立广.2011.多时间尺度环流对热带气旋海棠(0505)路径的影响［J］.气象科学，31(3):237-246.

田永祥.1994.非对称环流的细致结构与台风路径的摆动［J］.南京气象学院学报，17(4):399-404.

田永祥，炎利军，赵远东，等.2000.应用非对称结构理论制作台风路径预报［J］.南京气象学院学报，23(4):469-474.

曾文曲，王向阳.2001.分形理论与分形的计算机模拟［M］.沈阳:东北大学出版社.

张济忠.1995.分形［M］.北京:清华大学出版社.

赵大军，于玉斌，李莹.2011.“0814”号强台风发展维持的环境场分析［J］.气象科学，31(5):591-597.

周伟灿，王灿伟.2009.两类登陆热带气旋的大尺度环流特征分析［J］.大气科学学报，32(4):474-482.

Carr L E，Elsberry R L.1998.Objective diagnosis of binary tropical cyclone interactions for the western Pacific basin［J］.Mon Wea Rev，126:1734-1740.

Chan J C L，Gray W M.1982.Tropical cyclone movement and surrounding flow relationships［J］.Mon Wea Rev，110:1354-1374.

Chen L，Luo Z.1995.Effect of the interaction of different scale vortices on the structure and motion of typhoons［J］.Adv Atmos Sci，12:206-214.

Chen L，Luo Z.2006.The effect of interaction between meso-scale system and typhoon on its motion and structure change［C］//Preprints of 27th Conf.on Hurricanes and Tropical Meteorology.Monterey，CA:Amer Meteor Soc.

Elsberry R L.1995.Global perspectives of tropical cyclones［R］//World Meteorological Organization WMO-/TD.693，Rep.TCP-38，289.

Elsberry R L.2007.Recent advances in tropical cyclone track forecasting techniques that impact disaster prevention and mitigation［C］//International Training Workshop on Tropical Cyclone Disaster Reduction，WMO，CASWGTM.Guangzhou，China:WMO:1-7.

Enagonio J，Montgomery M T.2001.Tropical cyclogenesis via convectively forced vortex Rossby waves in a shallow-water primitive equation model［J］.J Atmos Sci，58:685-705.

Fiorino M，Elsberry R L.1989.Some aspects of vortex structure in tropical cyclone motion［J］.J Atmos Sci，46:975-990.

Luo Zhexian，Davidson N E，Ping Fan，et al.2011.Multiple-scale interactions affecting tropical cyclone track changes［J］.Advances in Mechanical Engineering，782590.doi:10.1155/2011/782590.

Maddox R A.1980.Meso-scale convective complexes［J］.Bull Amer Meteor Soc，61:1374-1387.