永磁直驱风电系统速度辨识方法分析及比较

李隆基， 耿华， 杨耕

（1.国网天津市电力公司电力科学研究院，天津> 300384;2.清华大学自动化系，北京 100084）

0 引言

近年来，风力发电已成为最具吸引力的清洁能源发电形式之一。由于成本低、效率高等特点，变速风力发电系统已得到广泛应用［1］。

在变速风电系统中，永磁直驱系统由于无齿轮箱、维护成本低且易于实现故障穿越而受到越来越多的关注与应用［2］。在永磁直驱风电系统的控制中，发电机转子转速和转子磁链位置信息至关重要。无论采用矢量控制还是直接转矩控制，转子转速信息均为转速闭环控制的关键反馈量;而在矢量控制中，转子转速、磁链位置更是坐标变换的前提。采用速度传感器可以获得转子转速信息，但随着机组容量的增加，转子轴径越来越大，许多厂家的发电机采用外转子结构以减小电机尺寸。速度传感器在这些场合难以安装，并为进一步提高系统可靠性、降低成本，因而当前的永磁直驱风电系统越来越多地采用无速度传感器控制策略。

目前已有大量文献对永磁同步发电机的转子转速与磁链位置的辨识方法作了深入研究，并且其中部分方法已应用于商业化风电机组。常用的方法有以下几种：第一，基于反电动势的方法，如磁链积分法［3］（flux integration algorithm，FIA）、反电动势锁相环法［4］（EMF phase-locked loop，EPLL）;第二，基于观测器的方法，如扩展卡尔曼滤波器（extend Kalman filter）、简化的卡尔曼观测器［6］（simplified Kalman observer，SKO）;第三，基于模型参考自适应的方法，如端电压锁相环［5］（voltage phase-locked loop，VPLL）。尽管已有的大量文献对上述方法的设计步骤和性能分别作了深入探讨，但针对各种方法的动稳态特性、参数依赖性等性能的综合对比还未见报道，而不同方法的差异对风电厂商辨识方案的选择具有极其重要的意义。

本文从实际应用的层面分析并比较了以下4种方法的特性：FIA、EPLL、VPLL、SKO。FIA 法构建了纯积分器，通过发电机端电压、电流直接求得转子磁链位置，进而得到转子转速［3］。EPLL法是一种典型的基于反电动势的方法，该方法通过闭环随时调整辨识转子磁链的位置［4］。VPLL法由定子电压矢量位置求得定子磁链位置，再通过自适应调节器的补偿得出转子磁链位置［5］。SKO法采用简化的扩展卡尔曼滤波器辨识转子转速与磁链位置［6］。本文建立系统的小信号线性化模型，以对比不同算法稳态特性的差异。通过时域仿真和硬件实验，比较了辨识精度并且进一步揭示了不同算法下系统的动态性能、算法复杂度、参数依赖性及对系统的影响。

1 系统结构

永磁直驱风电系统典型结构如图1所示，包括两个子系统：机械系统与电气系统。机械系统包括风力机及其桨距角和偏航角的控制系统等;电气系统包括永磁同步发电机、全功率变流器及其控制系统等。在全功率变流器中，网侧逆变器控制直流母线电压以平衡机侧输出的有功功率;机侧整流器控制发电机的电磁转矩实现特定的控制目标，例如恒功率输出［3］、最大功率点跟踪［4］等。

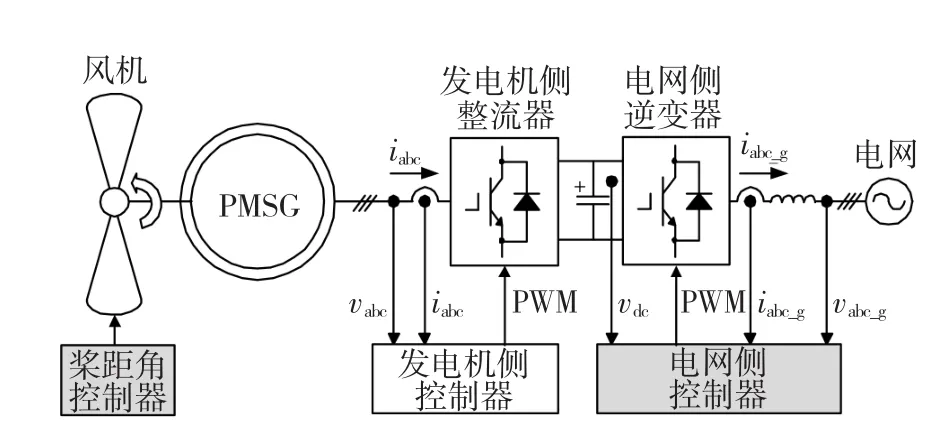
图1 永磁直驱风电系统的结构图Fig.1 Configurations of PMSG based WECS

永磁同步发电机在两相静止α-β坐标系下电压方程的数学模型为

其中：Rs为定子电阻;Lα=Lβ=1.5L（L为定子自感与互感的差）;ψ'r=ψr（ψr为转子磁链的幅值），ωr为真实的电角速度，θr为真实的磁链位置。

式（1）在转子磁链定向的条件下，经变换后两相d-q旋转坐标系下电压方程的数学模型为

其中，Ld=Lq=1.5L。如果考虑式（1）与式（2）中的转子转速ωr为未知变量且磁链位置θr为ωr的积分，则估计量与可由定子电压、电流推导得出，即转速、磁链位置在理论上是可由检测的发电机侧信息辨识的。

发电机侧整流器的控制结构如图2所示。在以转子磁链定向的d-q轴坐标系下，采用d轴电流为0的控制方法。由于q轴电流与发电机的转矩成正比，故可实现转矩（或转速）的解耦控制。

发电机的转子转速与磁链位置信息由发电机端电压与定子电流估计得出。辨识出的转子转速、磁链位置信息用于发电机侧整流器的转矩控制，以及上位机对整个风机的控制。下节重点通过分析4种辨识方法的小信号线性化模型，以分析4种辨识方法的不同。

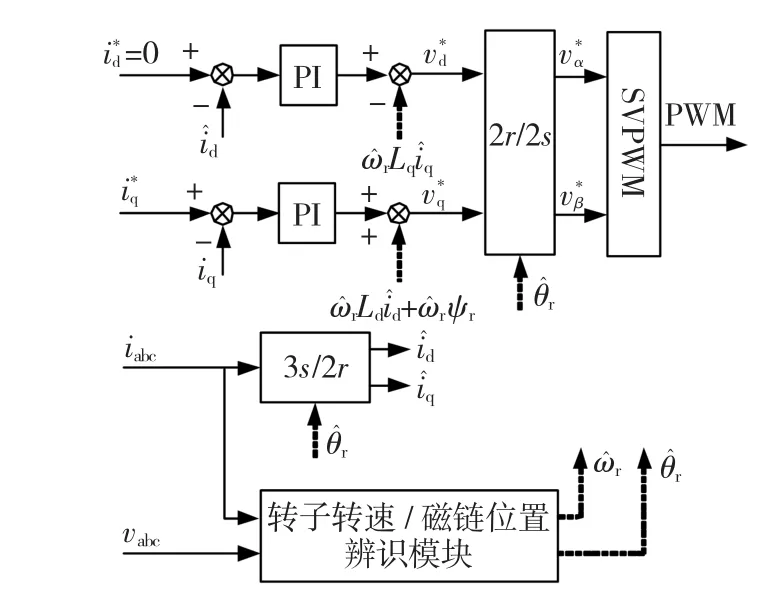
图2 发电机侧整流器控制框图Fig.2 Control diagram of generator-side converter

2 四种速度辨识策略及分析

四种速度辨识策略的结构与框图如图3所示。

2.1 FIA法

在FIA算法的纯积分器中，PI调节器用于生成转子磁链幅值的补偿量，可写作［3］

该积分器具有自适应性，可自行调节转子磁链的补偿量，从而使初值与零漂等问题得到解决［3］。在图3（a）、图3（b）中，ψα、ψβ为定子磁链，ψrα、ψrβ为转子磁链，ωc为积分器中反馈环节滤波器的截止频率。

FIA法可在系统允许的转速变化范围内应用［3］。纯积分器模块的前向通道和反馈通道均有低通滤波器，其截止频率ωc的设计对积分器乃至整个模块的动态特性均至关重要。尽管FIA法直接得到转子磁链位置，但由于积分器的滞后特性仍可能导致响应时间较长。

2.2 EPLL法

EPLL在两相旋转d-q坐标系下实现，如图3（c）所示。辨识出的转子转速、磁链位置越稳定，发电机电流的谐波越少。PI调节器与反正切函数可抑制环外扰动，如 uabc、iabc。磁链位置误差描述为［7］

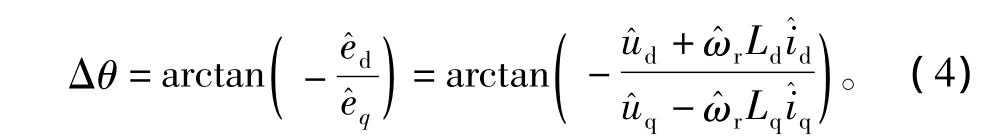
EPLL由于只有一对PI参数，故其相比其他3种方法更为简易。在EPLL的空载试验中，仅需测试辨识转子转速的阶跃响应。

2.3 VPLL法

VPLL是另一种锁相环的方法，如图3（d）所示。与EPLL用到反电动势不同，VPLL直接将发动机端电压变换至d-q坐标系。为得到转子磁链位置，需由端电压矢量位置求得的定子磁链位置再进行功率角的补偿。d轴电压指令参考值可以表述为［5］

图3 四种辨识策略图Fig.3 Four identification schemes

2.4 SKO法

SKO法是一种简化的扩展卡尔曼滤波器，如图3（e）所示。SKO法包括一组降维的状态变量与常量增益矩阵，且极易在数字处理器中实现［6］。在式（6）中，SKO的原理与EPLL和VPLL相同。SKO是4种辨识算法中最简易的策略，通过实验验证：SKO的算法复杂度仅为FIA法的一半。

其中：ε为辨识磁链位置误差;w为中间计算量;k1～3为观测器参数;k为数字控制的迭代次数。

2.5 不同无速度传感器控制算法的稳态特性分析

整个风电系统具有强非线性特性，不同辨识算法对系统运行性能的影响难于直接分析，故本文基于线性化小信号模型分析系统的稳态性能。在图2的基础上加入发电机转子转速外环，转速指令由数字控制器给定，分析以上4种辨识策略参与发电机侧整流器控制的不同效果，如图4所示［8］。

图4 发电机侧控制系统框图Fig.4 Generator-side control diagram

图4所示的发电机侧控制系统可分为3部分模型，即发电机、转速/转矩双闭环控制器及辨识模块的数学模型，分别建立三者的状态方程为

其中，xg=［idiqωrθr］T为发电机模型的状态变量，xc=［xASRxdACRxqACR］T为控制器模型的状态变量，xo为辨识模块的状态变量;ug、uc、uo为三者输入量。鉴于篇幅有限，本文不赘述以上表达式。

若将图4中给定转速指令为常数，分析发电机侧控制系统对输入原动转矩TL扰动的特性，那么可将图4描述为如下系统，如图5所示。

图5 发电机侧控制系统Fig.5 Generator-side control system

根据式（7）所列模型描述、图5所示三者模块之间输入输出关系，可列出图5的状态方程为

分析输入为原动转矩TL、输出为辨识转速和磁链位置的系统幅频特性，如图6所示。3者均采用标幺值表示，且基值分别为：TLN及2π。在恒转速控制的稳态下，不同辨识策略下系统输出对输入的增益不同。这样，4种方法对发电机电流（或转矩）的控制效果便存在差异。

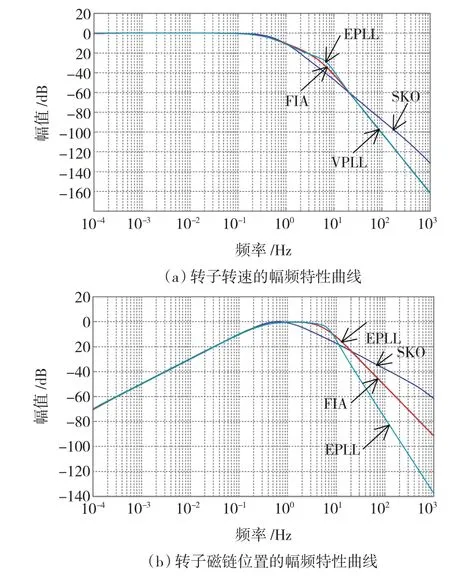
图6 转子磁链位置的幅频特性Fig.6 Magnitude-frequency character of rotor speed and flux position

在图6（a）的转子转速幅频特性曲线中，4种方法的低频段特性基本相同，均为0 dB;但在大于1 Hz的中高频段，4种方法的特性曲线出现不同。在1 Hz至20 Hz的中频段上，EPLL法的增益略大于FIA法与VPLL法，且大于SKO法。但在大于20 Hz的高频段上，SKO法的幅频特性曲线的衰减速率小于其他3种策略，以至于SKO法的高频段增益明显大于其他3种策略。

图6（b）中转子磁链位置的幅频特性曲线低频段基本相同;在大于1 Hz的中高频段中，4种方法的特性曲线不同。在大于20 Hz左右的高频段中EPLL相比VPLL、FIA出现明显差异，即幅值增益小于后两种策略;而 SKO法的幅值增益仍为4者最大。

FIA法、EPLL法、VPLL法及 SKO法4种策略由图6（a）、图6（b）的曲线可以看出，转子转速与转子磁链位置不存在直接的关系，即4种方法在相同频率下转速、磁链位置的顺序关系并非一致。这种中高频段4种策略的差异，具体如何影响系统控制效果及其规律将在下一节通过仿真与实验进行讨论。

3 仿真与实验

本节通过SIMULINK时域仿真与硬件实验，一方面验证上节的稳态特性分析，具体包括转子转速的辨识精度、磁链位置的辨识精度以及对系统控制效果的影响;另一方面比较不同辨识方法的动态性能、算法的复杂度以及参数的依赖性等内容。

3.1 稳态特性的时域仿真与硬件实验

在时域仿真中，本文建立了永磁直驱风电系统的SIMULINK模型。系统结构如图1所示，机侧控制如图4所示，网侧采用电网电压定向的矢量控制。为公平比较，4种辨识方法控制下，闭环系统运行状态为相同的转速、相同的负载，其参数均调至使得辨识转速响应相同。并且各系统的矢量控制参数也均保持一致，使4种方法的比较在系统运行效果均较好的情况下进行。图7、图8分别为4种辨识转速、真实转速的比较和4种辨识磁链位置误差的比较。

从图7、图8所示的仿真结果上可以看出，辨识转速与磁链位置的关系不一致。由于转速与磁链位置的积分关系，即使辨识转速有较大误差波动，但若转速误差曲线与误差零轴所包围的面积较小，磁链位置误差便会较小。转速误差、磁链位置误差以及电流总谐波含量（THD）如表1所述。

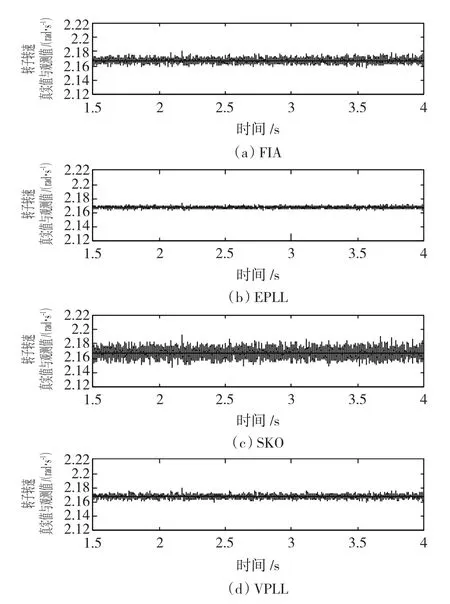
图7 四种辨识转速、真实转速的比较Fig.7 Identified and real speeds comparison

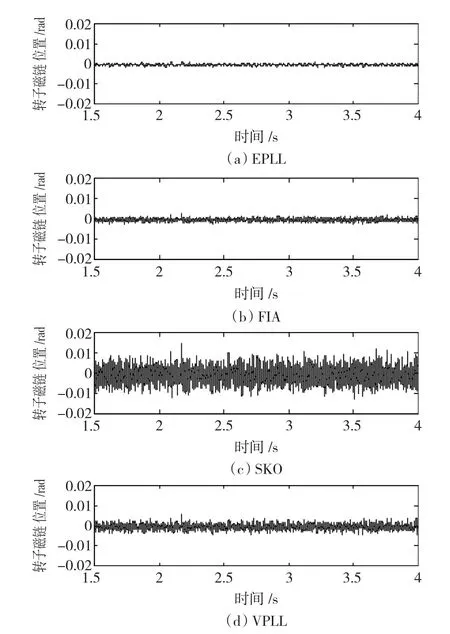
图8 四种辨识磁链位置误差的比较Fig.8 Identified rotor position errors comparison

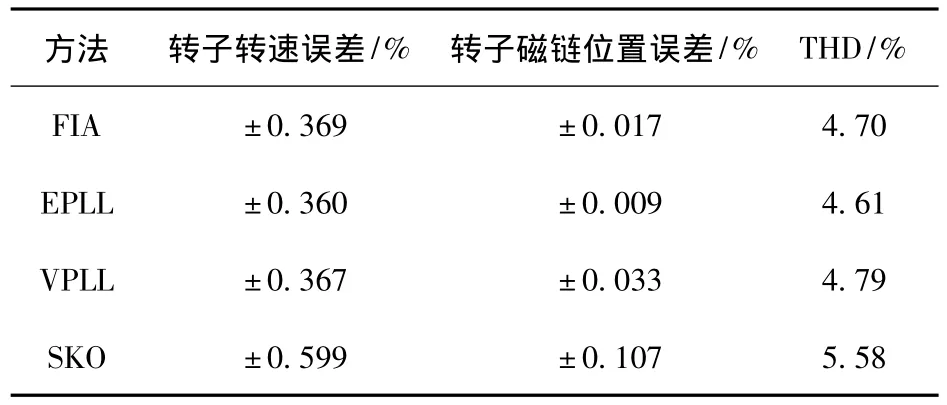
表1 稳态特性的时域仿真比较Table 1 Static character comparison on time-domain simulation

本文的硬件实验在永磁直驱风电系统平台上进行，风力机由带变频器调速的异步电机模拟。实验系统容量15 kVA，发电机参数额定容量15 kW，额定转速180 r/min，额定电压400 V，极对数16，转子磁通1.8 Wb，定子电阻 1.25 Ω，定子电感 9.37 mH。4种方法分别作系统辨识部分后的稳态控制效果如图9、图10所示，其稳态运行时的电机转速为67.7 r/min，负载转矩为97.8 N·m。

4种辨识方法下发电机三相电流的频谱分析如表2。每种方法控制下，最大的谐波含量为偶次谐波，尤其是二次谐波。原因在于发电机定子电压、电流采样环节使用的单极性AD模块造成直流偏置，进而在d-q变换后产生了二次谐波。由图10和表2可见，SKO法下系统对偶次谐波的抑制能力最差。

图9 稳态时辨识的转子转速、转速误差、磁链位置、磁链位置误差（四种方法均运行在同一工作点）Fig.9 Steady-state identified rotor speeds，identified rotor speed errors，identified rotor flux positions，and identified rotor flux positions errors（These comparisons are based on a specific operation point）

图10 四种辨识模块控制下的发电机电流Fig.10 Generator currents controlled on the four identified modules

表2 图10的电流谐波分析Table 2 Current harmonics analysis of Fig.10

磁链位置误差与电流谐波THD的对比如表3所示。可见辨识的磁链位置误差越大，控制下的电流谐波THD越大。磁链位置误差直接决定了系统的运行特性。在矢量控制中，磁链位置信息被用作坐标变换。故为获得更平稳的转矩应使得电流谐波THD尽量小，即需减小辨识磁链位置的误差。

表3 实验的控制效果对比Table 3 Experimental control effect comparisons

3.2 动态特性及其他的时域仿真与实验

给定驱动器频率突变指令测试4种辨识方法的动态响应，如图11所示。虽然实验的转速动态特性与仿真不同，但磁链位置误差与系统控制效果的关系相同，这同样可佐证第3节的分析结果。其中由于FIA中纯积分器的作用，辨识的转子转速误差动态过渡过程中，相比其他方法相位滞后90度。

图11 空载条件下辨识转速、转速误差的动态特性Fig.11 Identified speeds and errors dynamic responses with non-load

本文通过比较定子电感发生±25%变化时的运行特性，对比4种方法的参数依赖性。根据图12对比的结果：如果辨识模块中的电感参数比实际参数小，那么辨识出的转子磁链位置比真实位置滞后;反之亦然。虽然该4种方法均依赖于发电机的参数，但该4种方法对参数的依赖性仍可根据仿真结果得出由弱至强依次为 SKO、EPLL、VPLL、FIA。

图12 电感参数变化时的转子磁链位置误差（±25%L）Fig.12 Position errors at parameter variations（±25%L）

关于4种方法的算法复杂度比较，尽管以上仿真均基于离散模型建立并实现，但发电机模型与电网模型仍为理想模型。故实验中比较算法复杂度相比仿真更有实际意义，故在模块参数调节合适后，算法复杂性可从实验结果中对比。4种辨识算法分别在实验平台DSP2812上运行的结果如表4所示，通过计算执行一遍算法程序所需的机器周期数以量化算法的时间复杂度。由于该4种算法所用变量（程序中所需寄存器）均较少，故算法的空间复杂度不是制约该4种辨识方法实际应用的方面。从表4的实验结果可以得出以下结论：FIA法是最复杂的算法，而EPLL法与VPLL法的复杂度相似，均比FIA法简易。SKO法是4种方法所花费机器周期最少的策略，但其控制效果过差以至于无法实际应用。

表4 实验的机器周期数对比Table 4 Experimental machine cycles comparisons

综合3.1小节、3.2小节时域仿真和硬件实验的分析，4种辨识方法的全面对比如表5所示，其中○表示该算法在该指标下的性能优劣程度，×表示该算法在该指标下的性能最差。

表5 四种方法对比的总结Table 5 Summary of four schemes

4 结语

本文比较了4种用于永磁直驱风电系统的无速度传感器辨识方法。由于4种方法与整个系统的非线性特性，本文在分析不同方法特点后建立了系统的小信号线性化模型，以比较不同算法稳态特性的差异。在分析得出不同算法下系统对输入转矩扰动不同的结论后，搭建了时域仿真和硬件实验，并且验证了文中分析的结果。为进一步分析不同辨识算法，本文给出了动态特性、算法复杂度、参数依赖性的对比结果。最后，经全文分析得出：FIA法由于算法复杂性限制了其实际应用;VPLL法的参数较难调试，且控制效果差于FIA法、EPLL法;SKO法在4种方法中控制效果最差。相比以上3种方法，EPLL法由于其有效性且易于实际数字控制器实现，故其为适用于兆瓦级永磁直驱风电系统无速度传感器控制策略的转子转速、磁链位置辨识策略。

［1］ CARRASCO J，FRANQUELO L，BIALASIEWICZ J，et al.Power-electronic systems for the grid integration of renewable energy sources：A survey［J］.IEEE Transactions on Industrial Electronics，2006，53（4）：1002-1016.

［2］ GENG Hua，XU Dewei，WU Bin，et al.Active damping for PMSG-based WECS with DC-link current estimation［J］.IEEE Transactions on Industrial Electronics，2011，58（4）：1110-1119.

［3］ HU Jun，WU Bin.New integration algorithms for estimating motor flux over a wide speed range［J］.IEEE Transactions on Power E-lectronics，1998，13（5）：969-977.

［4］ HU Shuju，XU Honghua.Research on sensorless control based back-to-back converter for direct-driven WECS［C］//Power and Energy Engineering Conference，March 27-31，2009，Wuhan，China.2009，1：27-31.

［5］ 汪令祥，张兴，张崇巍，等.兆瓦级永磁同步风力发电机无速度传感器矢量控制方法研究［J］.电工电能新技术，2009，28（4）：19-22.

WANG Lingxiang，ZHANG Xing，ZHANG Chongwei，et al.A sensorless vector control method for MW level permanent magnet synchronous generator［J］.Advanced Technology of Electrical Engineering and Energy，2009，28（4）：19-22.

［6］ GONZÁLEZ L G，FIGUERES E，GARCERÁ G，et al.Synchronization techniques comparison for sensorless control applied to wind energy conversion systems（WECS）［C］//2009 13th European Conference on Power Electronics and Applications，September 8-10，2009，Barcelona，Spain.2009，1：1-9.

［7］ 胡书举，王剑飞，赵栋利，等.无速度传感器控制永磁直驱风电变流器的研制［J］.电机与控制学报，2009，13（4）：67-72.

HU Shuju，WANG Jianfei，ZHAO Dongli，et al.Development on sensorless control based back-to-back converter for direct-driven WECS using PMSG［J］.Electric Machines and Control，2009，13（4）：67-72.

［8］ LI Longji，GENG Hua，YANG Geng，et al.Comparisons of four rotor speed identification schemes for PMSG based WECS［C］//2011 International Conference on Electrical Machines and Systems，August 20-23，2011，Beijing，China.2003，1：1-9.

（编辑：刘琳琳）