一种H桥级联型PWM整流器的电容电压优化平衡控制

武琳， 刘志刚， 洪祥， 李耀华

（1.北京交通大学电气工程学院，北京 100044;2.中国科学院电工研究所，中国科学院电力电子与电气驱动重点实验室，北京 100190）

0 引言

H桥级联整流器 （cascaded H-bridge rectifier，CHBR）是一种以H桥电路作为基本能量变换单元，多个H桥单元级联构成的拓扑结构。该电路以耐压相对较低的功率器件来实现较高电压级别的能量转换，具有结构模块化，控制简单，拓展性好的特点。使用H桥级联的变换器已经成功应用于静止同步补偿器（static synchronous compensator，STATCOM）［1］，固 态 变 压 器 （solid state transformer，SST）［2-3］，电 力 机 车 牵 引 （locomotive traction，LT）［4］有 源 电 力 滤 波 器 （activepowerfilter，APF）［5］，风力发电 （wind power generation，WPG）系统［6-7］等场合。

H桥级联型整流器中n个H桥单元的直流侧电容相互独立，维持各独立电容器的电压均衡是保证整个系统可靠运行的前提，也是低耐压的功率半导体器件应用于高压场合的基础。因此H桥级联整流器的电容电压均衡控制一直是该拓扑的研究热点。已有的电压平衡控制算法，基本分为基于电压反馈和基于能量反馈的电压平衡控制两种。

文献［8］讨论了几种采用电压环和电流环的双闭环控制结构，通过对每一路整流器的输出电压都进行闭环控制，实现了对电压的平衡控制，缺陷在于在级联级数比较多的时候，控制器的参数选择比较困难，并且不能实现空载运行。文献［9-10］采用了一种基于D-Q变换的整流器直流电容均压控制方法，该方法将静止坐标系下的变量变换到旋转坐标系下。该方法的优势在于旋转坐标系下被控参数变为直流分量，按照直流变换器的设计方法来设计控制器。缺陷在于切载时只有实轴电流为实际值，虚拟轴电流在1/4工频周期后才能做出响应，这种固有的滞后会影响整个系统的动态响应速度，使系统不能对切载和扰动做出迅速响应。文献［11-12］针对直流电容电压的不平衡问题，以系统能量作为控制目标，提出了一种无源性控制的电压平衡方法，不仅实现了电压平衡，还能够保证系统的稳定性。缺陷在于控制算法复杂，运算量较大。文献［13-14］根据各级电容电压的高低来实时确定各级电容的充放电状态，从而选择相应的开关状态，这种方法实现简单，缺陷在于采用的滞环比较的电流控制带来了开关频率不恒定的情形，难以实现数字化控制。

本文以H桥级联型整流器为研究对象，通过对基于电容电压的高低排序来确定各级电容充放电状态的电压平衡控制算法进行分析，提出了一种电容电压优化平衡控制策略，在该策略下，每个电网周期内，H桥模块的平均投切次数减少，相应的开关器件的动作次数也得到降低。仿真和实验验证了文中所提出控制策略的正确性和可行性。

1 H桥级联型整流器拓扑及数学模型

基于H桥级联的整流器结构如图1所示，n个单相H桥PWM整流器的输入端以级联的形式连接起来，通过交流电感Ls和电网连接。

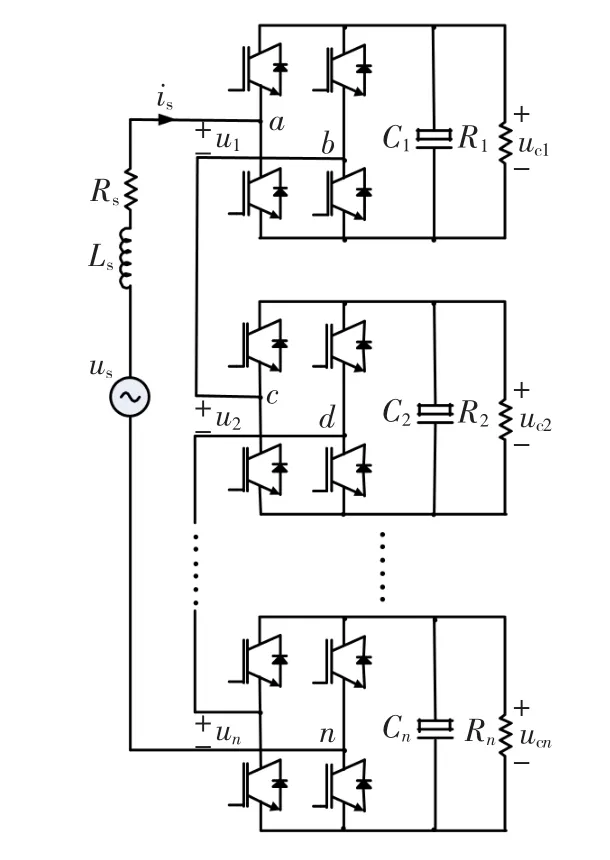
图1 H桥级联型整流器拓扑Fig.1 The structure of cascaded H-bridge rectifier

由开关函数 Si，i=1，2，…，n，可以得到该拓扑的数学模型。

式中：us，is分别为电网电压和电流;Ls为交流侧电感;uan为整流器交流侧级联电压;Ck，Rk，uck分别为各级联单元的直流母线电容、负载及输出电压。k=1，2，…，n。一般取 C1=C2=… =Cn=C。

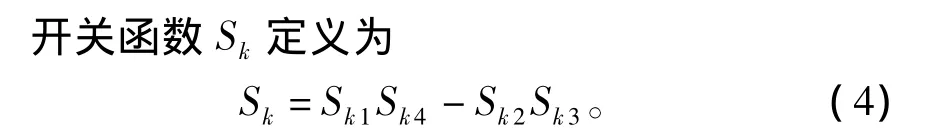
其中Sk1～Sk4∈{1，0}，为第 k级 H 桥单元4个开关管的工作状态。由上图可知，开关函数Sk有1，0，-1三种取值，则对应的H桥有uck，0，-uck3种电平输出［15］。

2 H桥级联型整流器PWM调制方式及其控制方式分析

2.1 PWM调制方式

H桥级联型整流器的每一个H桥单元均为电压型单相PWM整流器，对H桥整流器的基波电压的控制，可以通过双极性调制和单极性调制两种方式来实现。图1的第k个H桥单元工作在双极性模式下时，交流侧输出在uck，0，-uck3个电压下不断切换，而在单极性调制模式下，交流侧输出在uck与0或者-uck与0之间两个电压下不断切换。和双极性调制方式相比，单极性调制下功率器件的开关损耗和电网电流谐波更小［16］，在本文中采用单极性PWM调制方式。

2.2 H桥级联整流器的控制方式

文献［13］提出了一种基于各H桥单元电容电压的高低来实时确定各级电容的充放电状态，从而实现电压平衡的控制策略。该控制方法的内环采用了电流滞环结构，这种基于滞环比较的电流控制方法具有电流相应速度快的特点，缺陷在于变化的开关频率带来了开关损耗的增大，同时给滤波器的设计带来不变，也难以实现数字化控制。

为了实现开关频率的恒定，本文采用了电压外环的PI控制和电流内环的比例-谐振（PR）控制的双环控制方式，将得到的交流参考电压u*an与频率恒定的载波相比较，以单极性PWM调制来实现电压平衡控制的目的。整流侧的闭环控制框图如图2所示。图2中u*sum为各级联单元直流电压之和的参考值，θ为电网电压us相位角，G1（s），G2（s）分别为电压环PI控制器和电流环PR控制器。

图2 整流器闭环控制框图Fig.2 The structure of closed-loop control of rectifier

3 电容电压平衡控制策略的优化

若uc1=uc2=…=ucn=Uc，每个H桥单元随着开关状态的不同，输出Uc，0，-Uc3种电平，n个H桥级联时，变流器的电平组合共有0，±Uc，±2Uc，…，±2n Uc，共计2n+1种。

假设电路结构由n个H桥单元级联而成，首先将检测到的交流侧电压参考电压分成n个区间，随着电压的变化，它所在的区间也会发生变化。交流侧电压所在区间的示意图如图3所示。

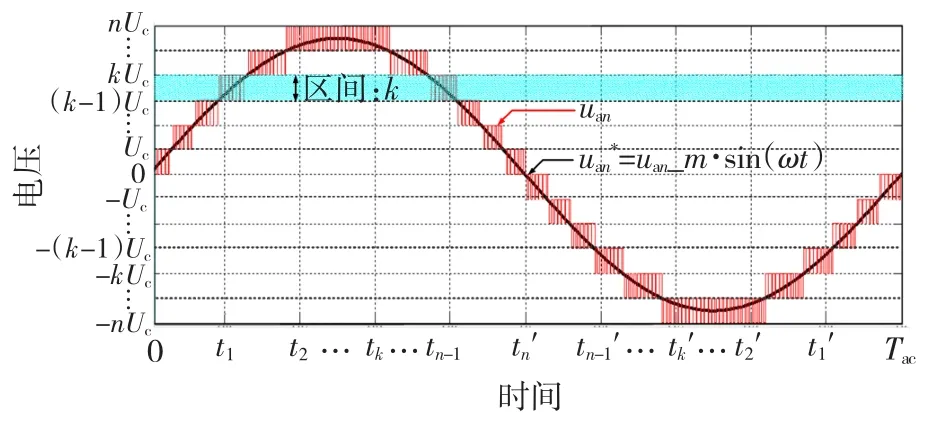
图3 交流侧输入电压的分区Fig.3 Input voltage regions of AC side

3.1 传统的电容电压平衡控制

在每个采样周期内，H桥单元根据需要输出Uc，0，-Uc，PWM调制共4种状态。在进入每个采样周期时，根据整流器所要输出的电压及输出电流正负，判断直流侧电容的能量交换情况，在充电状态时，将直流侧电容电压uc1，…，ucn由低到高排序，选择投入H桥单元时，根据排序结果从电压较低的开始，直到满足输出电压要求为止;放电则反之。

决定各H桥级联单元的电容电压状态的控制算法流程图如图4所示，图中+1，0，-1，PWM分别代表了H桥单元的正投入，切除，反投入，PWM调制，也即是 Uc，0，-Uc，PWM 调制共4种状态。

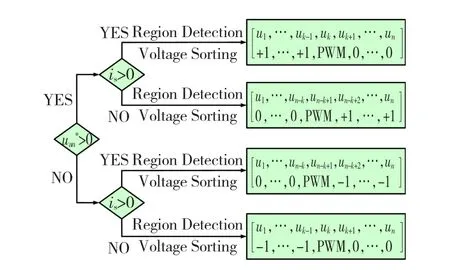
图4 控制算法流程图Fig.4 Flow chart of control algorithm

通过不断的改变H桥单元的充放电状态，就可以达到使各个H桥单元的电容电压保持平衡。双闭环结构使得各电容电压之和为nUc，通过控制器将各H桥单元的电容电压达到一致，因此每个H桥单元的直流电容电压都会稳定在参考电压Uc附近。

3.2 电容电压的优化平衡控制

在3.1节中采用的H桥级联整流器的直流电容电压的平衡控制，是根据电容电压大小排序的结果，来决定电容充放电优先顺序，这种方式没有考虑到降低开关器件开关频率的要求。在高频化的场合下必然带来开关损耗的增加。为了减少开关损耗，采用优化的控制算法，通过减少H桥单元状态切换的次数，来减小器件动作的频率，是一种可行的方式。

在3.1节中采用的电容电压平衡控制的控制目标是实现各H桥单元电容电压的完全一致，在本章所提出的优化控制方法中，电容电压平衡控制的目标调整为抑制各H桥单元电容电压相对其参考值的波动幅度。根据这种思路，在电容电压额定值附近设定一组电压上下限，将电容电压平衡控制的重点放在电压值越限的H桥单元上。对电容电压在电压值上下限范围内的H桥单元模块，H桥单元的投切保持在由电压值上下限之外进入电压值上下限之内时刻的状态。对电容电压超出电压值上下限范围的H桥单元模块，仍然采用3.1节所提出的电压平衡控制方法。这种优化控制方法的目的是在一定程度上使电容电压未越限的H桥单元模块在触发控制下一次动作时保持原来投切状态，降低了器件的开关频率。

具体的控制方法介绍如下：设定了系数ku，H桥模块电压的控制目标参考值 Uc，电压的上限Uc-up和下限 Uc-down。使

1）如果 H 桥单元电压 uc1，uc2，…，ucn处于［Uc-down，Uc-up］区间内，使H桥单元的投切停止，保持在各H桥单元由［Uc-down，Uc-up］区间之外进入［Uc-down，Uc-up］区间时刻的投切状态。在这种情况下，uc1，uc2，…，ucn的电压不再保持在 Uc附近，开始向［Uc-down，Uc-up］区间之外偏移。

2）如果 H 桥单元电压 uc1，uc2，…，ucn处于［Uc-down，Uc-up］区间之外，重新启动电压排序的电压平衡控制算法，H桥单元的投切恢复。在这种情况下，uc1，uc2，…，ucn的电压由［Uc-down，Uc-up］区间之外开始向［Uc-down，Uc-up］区间内偏移。

可以认为，在3.1节采用的均压控制算法是系数ku=0的一个特例。

优化的H桥级联单元的电容电压状态的控制算法流程图如图5所示。

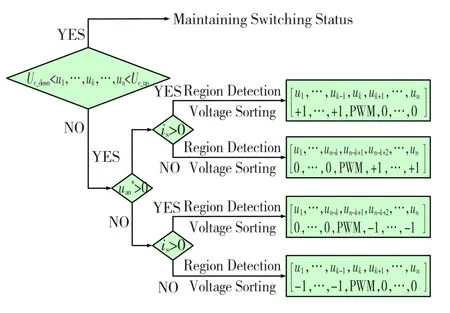
图5 优化的控制算法流程图Fig.5 Optimized flow chart of control algorithm

以上就是本文所提出的H桥级联型整流器的电容电压优化平衡控制策略。这种优化的控制策略不再是电压排序完成后，在下一个开关周期，根据排序结果直接决定各H桥单元电容的充放电状态。而是在各H桥单元电容电压超出了设定电压区间后，才启动均压控制。这种优化策略将平衡控制的重点放在电容电压偏离设定电压区间的H桥单元模块上。优化策略允许各H桥单元的电容电压在一定范围内之间存在一定的偏差，并通过引入电压的上下限使各H桥单元具有一定的保持原来投切状态的能力，以避免频繁地投切各H桥单元模块，从而实现降低器件开关频率的目的。

4 仿真与实验验证

4.1 仿真研究

为了验证所提出的H桥级联型整流器电容电压优化平衡控制策略的有效性，以两级级联的H桥整流器为研究对象，仿真取电网电压us=110 V，网侧电感Ls=4 mH，两个H桥单元的电容值C1=C2=4 mF，负载R1=R2=8 Ω，均压控制的目标为uc1=uc2=Uc=100 V，载波频率fs=2 kHz。图6和图7分别为传统的均压控制（即为ku=0）方法和选取ku=0.03时的优化均压控制算法所得到的直流电容电压的波形。

图6 ku=0时uc1和uc2的电压波形Fig.6 Waveforms of uc1and uc2as ku=0

图7 ku=0.03时uc1和uc2的电压波形Fig.7 Waveforms of uc1and uc2as ku=0.03

比较图6和图7中uc1和uc2的电压波形，在没有优化的电压平衡控制策略下，两个电压的波形始终保持一致，这表明2个H桥单元始终处于投切状态。采用了经过优化的电容电压平衡控制方法后，在电容电压为［97，103］的电压区间内，uc1和 uc2的电压差增大了，这表明在该区间内，均压控制算法被切除，2个H桥单元的投切状态保持固定。而在［97，103］的电压区间之外，uc1和 uc2的电压保持一致，这表明均压控制算法重新被投入。

要指出的是，系数ku的选取不是可以随意增大，ku的继续增大，可能会带来电压平衡控制算法失效。

4.2 实验验证

为验证所提出的优化电压平衡控制理论的正确性，搭建了两级级联的H桥整流器样机。实验参数和仿真参数完全一致。系统控制平台示意图如图8所示。

图8 H桥级联整流器电压平衡控制实验平台Fig.8 Experiment platform of voltage balance control for cascaded H-bridge rectifier

图9和图10分别为实验得到的传统的均压控制（即为ku=0）方法和选取ku=0.03时的优化均压控制算法所得到的直流电容电压的波形。

图9 ku=0时uc1和uc2的电压波形Fig.9 Waveforms of uc1and uc2as ku=0

图10 ku=0.03时uc1和uc2的电压波形Fig.10 Waveforms of uc1and uc2as ku=0.03

比较图9和图10中uc1和uc2的电压波形，可以看出，优化的电压平衡控制算法，并没有带来电容电压的大幅度波动。在图9中没有经过优化的均压控制下，两个电压的波形始终保持一致。而在图10中，采用了经过优化的电容电压平衡控制方法后，在电压为［97，103］的区间内，uc1和 uc2的电压不再保持一致，这表明在该区间内2个H桥单元的投切状态保持固定。而在［97，103］的电压区间之外，均压控制算法重新被投入，使得uc1和uc2的电压重新保持一致。

评估H桥级联整流器优化的电压平衡控制的重点是开关器件的动作频率和电容电压的波动幅度。表1给出了一个电网周期内，仿真和实验2种途径得到的未经过优化（ku=0）和经过优化的（ku=0.01～0.04）的电压平衡控制下H桥单元状态切换次数，开关器件的动作次数和电容电压的波动幅度平均值。

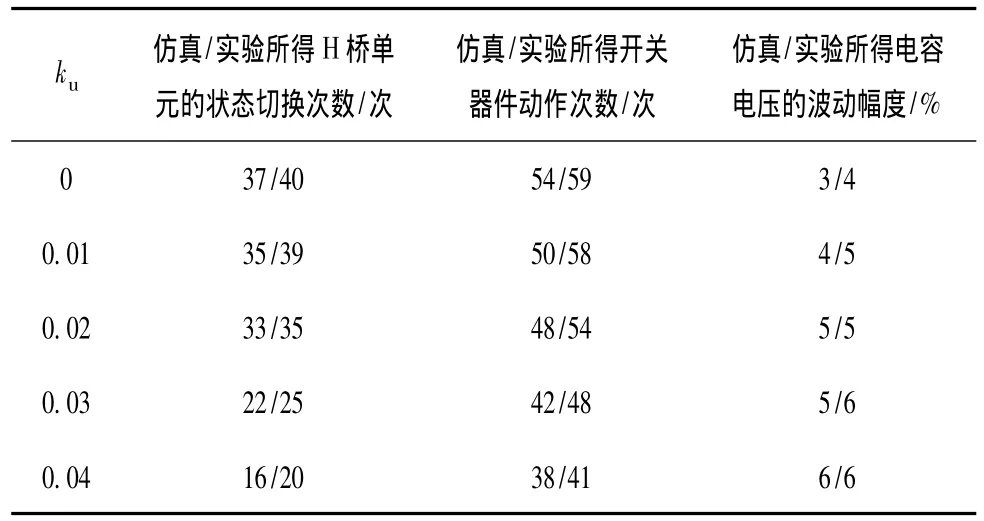
表1 不同ku值下H桥状态切换次数，器件的动作次数和电容电压的波动幅度Table 1 Number of H-bridge switching status，number of device switching and capacitor voltage fluctuation amplitude at different values of ku

由表1可以看出，经过优化的电压平衡控制算法，并没有带来H桥单元电容电压的大幅度波动，开关器件的动作频率随着系数ku的增加逐渐减小。也就是说，在没有显著增加电容电压波动的情况下，通过优化电压平衡控制算法来降低开关器件的动作次数的方法是可行的。

5 结语

本文以H桥级联型整流器为研究对象，通过对其拓扑的分析，并建立了对应的数学模型。在对H桥级联型整流器PWM调制方式和电容电压平衡控制策略分析的基础上，针对基于通过电容电压的高低排序来实时确定各级电容充放电状态的电压平衡控制算法带来开关器件动作频率较高的问题，提出一种电容电压优化平衡控制策略，该控制策略在不引起电容电压波动幅度显著增高的情况下，降低了开关器件的动作次数，从而使器件的开关损耗得到降低。仿真和实验验证了文中所提出控制策略的正确性和可行性。

［1］ BARRENA J A，MARROYO L.RODRIGUEZ M A，et al.DC voltage balancing for PWM cascaded H-bridge converter based STATCOM［C］//In Proc.IECON，Nov.6-10，2006，Paris，France.2006：1840-1845.

［2］ RONAN E R，SUDHOFF S D，GLOVER S F，et al.Application of power electronics to the distribution transformer［C］//Proceedings of the 15th Annual IEEE Applied Power Electronics Conference and Exposition，Feb.2-10，2002，New Orleans，LA，USA.2000：861-867.

［3］ HUANG Alex Q.Renewable energy system research and education at the NSF FREEDM systems center［C］//2009 IEEE Power and Energy Society General Meeting，July 26-30，2009，Calgary，AB，Canada.2009：1-6.

［4］ BLAHNÍK，PEROUTKA Z，ZAK J，et al.Traction converter with medium frequency transformer for railway applications direct current control of primary active rectifiers［C］//Power Electronics and Applications，EPE’09.13thEuropean Conference on，Sept.8-10，2009，Barcelona，Spain.2009：1-8.

［5］ 李建林，张仲超，许洪华.基于级联H桥五电平变流器SAPF的应用研究［J］.电工技术学报，2006，21（2）：79-82.

LI Jianlin，ZHANG Zhongchao，XU Honghua.Research on SAPF based on cascade H bridge five-level converter［J］.Transactions of China Electrotechnical Society，2006，21（2）：79-82.

［6］ CARRASCO J M，BIALASIEWICZ J T，GUISADO R C P，et al.Power electronic systems for the grid integration of renewable energy sources：a survey［J］.IEEE Transactions on industrial electronics，2006，53（4）：1002-1016.

［7］ YANG C，LIANG H，JIANG J.Modeling and simulation of ACDC-AC converter for MW-level direct-drive system wind turbine interface grid［C］//37th IEEE Power Electronics Specialists Conference 2006，PESC＇06.June 18-22，2006，Jeju，Korea.2006：1-4.

［8］ DELL’Aquila A，LISERRE M，MONOPOLI V G，et al.Over

view of PI-based solutions for the control of DC buses of a singlephase H-bridge multilevel active rectifier［J］.IEEE Transactions on Industry Applications，2008，44（3）：857-866.

［9］ ZHAO Tiefu，WANG Gangyao，ZENG Jie，et al.Voltage and power balance control for a cascaded multilevel solid state transformer［C］//In Proc.Appl.Power Electron.Conf.Feb.21-25，2010，Palm Springs，CA.2010：761-767.

［10］ ZHAO Tiefu，ZENG Jie，BHATTACHARYA S，et al.An average model of solid state transformer for dynamic system simulation［C］//IEEE Power＆ Energy Society General Meeting，July 26-30，2009，Calgary，AB.2009：1-8.

［11］ DELL’Aquila A，LISERRE M，MONOPOLI V G，et al.Passivity-based control of a single-phase H-bridge multilevel active rectifier［C］//Proceedings of the 2002 28th Annual of the IEEE Industrial Electronics Society，Nov.5-8，2002，Sevilla，Spain.2002：3117-3122.

［12］ DELL’Aquila A，LISERRE M，MONOPOLI V G，et al.An energy-based control for an n-H-bridges multilevel active rectifier［J］.IEEE Transactions on Industrial Electronics，2005，52（3）：670-678.

［13］ IMAN-Eini H，SCHANEN J L，FARHANGI S，et al.A modular strategy for control and voltage balancing of cascaded H-bridge rectifiers［J］.IEEE Transactions on Power Electronics，2008，23（5）：2428-2442.

［14］ LIN B R，LU H H.New multilevel rectifier based on series connection of H-bridge cell［J］.Electric Power Applications，2000，147（4）：304-312.

［15］ DELL＇Aquila.MONOPOLI Vito，LISERRE Marco，et al.Design of H-bridge multilevel active rectifier for traction systems［C］//Industry Applications Conference，2002.37thIAS Annual Meeting，Oct.13-18，2002，Pittsburgh，PA，USA.2002：1020-1027.

［16］ 杨秋霞，高金玲，荣雅君，等.单相光伏并网系统共模电流分析［J］.电网技术，2011，35（1）：180-185.

YANG Qiuxia，GAO Jinling，RONG Yajun，et al.Analysis on common mode current of single-phase grid-connected PV system［J］.Power System Technology，2011，35（1）：180-185.

（编辑：刘琳琳）