加权lp 范数LMS 算法的稀疏系统辨识

刘遵雄，秦 宾，王树成

华东交通大学 信息工程学院，南昌330013

1 引言

自适应滤波器广泛应用于回波消除、噪声对消、系统辨识、自适应信道均衡等诸多领域中[1-5]。根据对输入信号和参考信号的不同定义，自适应滤波器应用分为四种类型[6-7]：系统辨识、逆模型、预测和干扰消除。

自适应滤波算法是自适应滤波器设计的核心。常用的自适应算法主要包括最小均方算法（LMS）、递归最小二乘方法（RLS）、神经网络算法[8-10]等，其中基于维纳滤波器理论的LMS 算法由于其结构简单，计算复杂度度低，性能稳定，易于实现等特点，仍是目前自适应滤波理论中应用最为广泛的算法。但是在实际应用中，许多待辨识的系统具有稀疏性，即冲击响应在时间域具有少量的非零值。对于稀疏系统辨识问题，LMS 算法无法很好解决，因为LMS算法没有充分运用冲激响应稀疏这一先验知识。随着LASSO[11]、压缩感知（Compressive Sensing，CS）等稀疏理论技术研究的不断深入和发展，在稀疏系统辨识方面相继提出零吸引最小均方算法算法（ZA-LMS）[12]、加权零吸引最小均方算法（RZA-LMS）[13]、l0范数惩罚的LMS 算法[14]。文献[15]首次提出加权l1范数惩罚求解最小化问题可以增强系统稀疏性。本文借鉴上述思想，提出了加权的lp(0 ＜p ≤1)范数惩罚的LMS 算法，并用于稀疏系统辨识，仿真结果验证了该算法的有效性。

2 系统辨识模型

系统辨识在信号处理、通信和控制等领域里都有重要应用，其实质上是根据系统的输入和输出信号来估计或确定系统的特性以及系统的单位冲激响应或传递函数。图1是一个系统辨识问题的框图。

图1 系统辨识模型图

一输入信号x(t) 经过一个未知系统h ，得到信号y′(t) ，由于叠加了环境噪声v(t) ，实际可测量的信号d(t)=y′(t)+v(t)作为自适应滤波器的参考信号，又称为滤波器的期望信号。

定义输入信号向量为：

则滤波器w 的输出可写为：

误差信号定义为期望信号与滤波器输出之间的差：

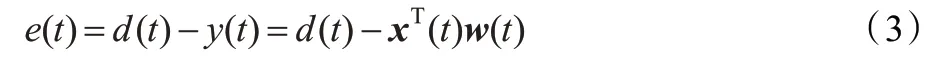
自适应滤波器w 使用输入信号x(t)和期望信号d(t)，用迭代的方法对未知系统h 进行辨识，当算法收敛之后，w就是一个h 的估计。

3 算法描述

3.1 lp(0 ＜p ≤1)范数惩罚LMS 算法

针对一般稀疏系统的基于lp范数(0 ≤p ≤1)约束的自适应算法核心思想，是根据未知系统的冲激响应稀疏的特点，在更新滤波器抽头权重的代价函数中施加稀疏性约束[12-14]。

研究表明，RZA-LMS 算法总体性能比ZA-LMS 算法有明显优势，这是因为RZA-LMS 算法惩罚函数更接近l0范数惩罚。如果p 取值接近0 时，lp范数惩罚函数近似l0范数惩罚，有代价函数如下：

其中，||⋅||lp表示p 范数，λlp＞0 为控制lp范数影响大小的平衡因子。和RZA-LMS 代价函数相似，当0 ＜p ＜1 时，代价函数具有共同的特性：非凸性、全局收敛性，以及相应的运算法则。但是lp(0 ＜p ＜1)范数惩罚的最小均方算法表现出更好的性能。式（4）求梯度，根据最速下降法得到相应权系数更新等式：

当p=1 时，文献[12]提出的零吸引最小均方算法（ZA-LMS）。系数向量更新等式为：

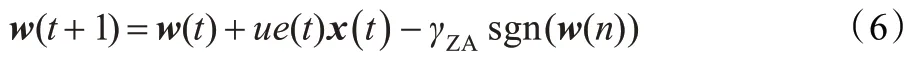
当0 ＜p ＜1 时，为了防止当输入信号向量为零或很小时算法不稳定，通常在上式中的分母上加上一个小的正常数ξlp，称为正则参数。于是得到lp(0 ＜p ＜1) 范数惩罚的LMS 算法的系数向量更新等式为：

3.2 加权lp(0 ＜p ≤1)范数惩罚LMS 算法

解决最小化问题时，在代价函数中引入加权的l1范数惩罚可以得到很好的稀疏作用，这一方法在稀疏的信号恢复得到实际应用。考虑到通常冲击响应稀疏的特性，如果lp(0 ＜p ≤1)范数惩罚的LMS 算法中加入一个更新权值，那么在稀疏系统辨识中会得到较好的仿真效果。相应的代价函数如下：

其中，λrlp＞0 为控制加权lp范数影响大小的平衡因子，更新权值：

ζrlp为设置的一个正则参数。

当p=1时，加权l1范数惩罚LMS算法的系数更行等式：

加权l1范数惩罚LMS 算法代价函数和RZA-LMS 算法、lp范数惩罚的LMS 算法不同的是其具有凸函数性质，保证在一定的范围内收敛于最小值。

当0 ＜p ＜1，由最速下降法导出加权lp范数惩罚LMS算法系数向量更新方程：

其中，γrlp=μλrlp，ξrlp设定为正则参数。式（4）和（8）中，λlp、λrlp的值选择影响惩罚LMS算法仿真实验的结果，它们的选择可以参考文献[13]。加权lp范数惩罚LMS算法过程，如图2。为了研究提出的稀疏惩罚LMS 算法，和已有的LMS、ZA-LMS 算法性能进行比较，通过仿真实验得到结果。

图2 加权lp 范数惩罚LMS 算法伪代码

4 实验分析

为了检验改进算法在系统辨识应用中的收敛速度和稳态误差两方面性能，本文设置了以下3 个仿真实验。

实验1 假设有限脉冲响应长度N=16，输入信号和观测噪声信号均为高斯白噪声，方差分别为σx=1 ，σv=1E-3。情况一：设置第8 个抽头权值为1，其他均为0，稀疏度1/16；情况二：情况一迭代200 次以后，随机设置8 个抽头权值非零，其他均为零，稀疏度8/16。5 个滤波器（LMS、ZA-LMS、lp(0 ＜p ＜1)范数惩罚LMS、加权l1范数惩罚LMS、加权lp(0 ＜p ＜1)范数惩罚LMS）各自运行200 次，其 中 lp范 数 中 p=1/2 ，其 他 参 数 设 置 μ=0.05 ，γZA=γlp=γrl1=γrlp=7.4E-4，ξlp=ζrlp=ζrl1=ξrlp=1。仿真实验结果如图3，从均方偏差MSD 结果可以看出，当系统稀疏时（前200 次迭代），加权的lp(0 ＜p ≤1)惩罚LMS 算法要比经典LMS 算法和lp(0 ＜p ≤1)惩罚的LMS 算法有较快的收敛速度和较小的均方偏差，并且p=1/2 时，加权的lp范数惩罚LMS 算法比加权l1范数惩罚性能更好。但是当系统非稀疏时，尽管加权lp范数惩罚的LMS 算法有较快的收敛速度，但是均方偏差MSD 比一般LMS 算法有所不足。

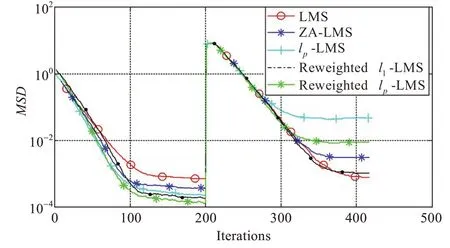
图3 白信号下算法收敛曲线

实验2 当p 接近于0 时，lp范数接近l0范数，越接近l0范数惩罚的函数，对于稀疏系统自适应滤波器的性能表现越好。如图4，p 分别取1/2 和3/4。当系统稀疏时（前200次迭代），加权l1/2范数惩罚LMS 算法收敛速度和稳态误差都有相对优势，但是当稀疏度有所提高时（后200 次迭代），加权l3/4范数惩罚LMS 算法和l3/4范数惩罚LMS 算法较其相对应的算法表现出较小均方偏差MSD和较慢的收敛速度。

图4 白信号下不同p 值的lp 惩罚LMS 算法收敛曲线

实验3 已知有限脉冲响应如图5，长度N=256，5 个滤波器分别迭代2 000 次，个别参数设置μ=0.005 ，γZA=γlp=γrl1=γrlp=1E-6，其他条件设置如实验1，仿真实验结果如图6。当p 的取值不同时，得到仿真结果如图7。从图中可以看出，加权的lp(p=1/2) 范数惩罚的LMS 算法相比较已有的稀疏LMS 算法在收敛速度和稳态误差方面都有较好的表现，并且p 在一定范围内取值越小表现的更为突出。

图5 稀疏系统的冲击响应

图6 稀疏系统和白信号条件下算法收敛曲线

图7 稀疏系统和白信号条件下不同p 值的lp-LMS算法收敛曲线

5 结论

针对稀疏的系统辨识问题，本文提出了一种改进的稀疏系统辨识方法——加权的lp(0 ＜p ≤1)范数惩罚LMS 算法。仿真实验结果表明：对于稀疏的系统，改进算法的收敛性和稳态性有明显提高；在[1/2，1]范围内p 取值越小，自适应滤波器的性能也就相对较好。 p 在（0，1/2）区间内步长参数的选择，将是下一阶段的重点研究问题。

[1] Bershad N J，Bermudez J C M，Toumere J Y.Stochastic analysis of the LMS algorithm for system identification with subspace input[J].IEEE Transation on Signal processing，2008，56（3）：1018-1027.

[2] 刘艳玲，邱丙益，樊长江.基于LMS 算法的卫星通信回波抵消方法[J].船舶电子工程，2007，27（6）：100-102.

[3] 孙永国.稀疏路径回波对消自适应并法的研究[D].成都：四川大学，2006.

[4] 陈立峰.自适应声回波抵消算法的研究与实现[D].厦门：厦门大学，2006.

[5] 赵亮，朱维庆，朱敏.一种用于水声相干通信系统的自适应均衡算法[J].电子与信息报，2008，30（3）：648-651.

[6] Haykin S.Adaptive filter theory[M].4th ed.Upper Saddle River，NJ：Prentice Hall，2002.

[7] Diniz P S R.自适应滤波算法与实现[M].2版.刘郁林，景晓军，谭刚兵，译.北京：北京电子工业出版社，2004.

[8] Widrow B，Hoff M E.Adaptive switching circuits[C]//Proceedings of the IRE WESCON Conference，1960：96-104.

[9] 孙锦华，金力军.几种改进型RLS 算法在自适应滤波系统中的应用[J].重庆邮电学院学报，2003，15（3）：14-15.

[10] 翁玉麟，邓长虹.自适应神经网络模糊推理系统最优参数的研究[J].计算机仿真，2005，22（8）：140-243.

[11] Fu W.Penalized regressions：the bridge versus the lasso[J].Journal of Computational and Graphical Statistics，1998，7（3）：397-416.

[12] 金坚，谷源涛，梅顺良.用于稀疏系统辨识的零吸引最小均方算法[J].清华大学学报：自然科学版，2010，50（9）：1312-1315.

[13] Chen Y，Gu Y，Hero A O.Sparse LMS for system identification[C]//Proc of IEEE ICASSP，Taipei，Taiwan，China，Apr，2009：3125-3128.

[14] Gu Y，Jin J，Mei S.l0norm constraint LMS algorithm for sparse system identification[J].IEEE Signal Processing Letters，2009，16（9）：774-777.

[15] Candes E J，Wakin M B，Boyd S P.Enhancing sparsity by reweighted l1minimization[J].Journal of Fourier Analysis and Applications，2008，14（5）：877-905.