基于表示的简单快速人脸识别方法

池义勇

(日东高速公路 临沂管理处，山东 临沂273400)

责任编辑:任健男

最近在模式识别领域，研究人员提出了一个有前景的图像识别方法，即所谓的稀疏表示法[1]，该方法没有利用传统的方式进行图像分类，而是首先使用训练样本子集的线性组合来表示测试样本，然后基于表达式的结果，对测试样本进行分类。这种方法已经获得了非常不错的性能，并且被一致认为是人脸识别研究的一个突破[2]。然而，稀疏表示法有非常高的计算开销，主要是因为它依赖迭代算法来实现解决方案。稀疏表示法也可用于乳腺癌的识别分类、信号处理及图像分解等[3]。

以前的人脸识别方法通常由特征提取、分类器的选择及分类这三个阶段组成。通常，特征提取阶段由变换方法实现，如基于独立成分分析方法[4]、主成分分析方法[5]和判别分析方法[6]。然而，稀疏表示法采用了引人注目的新的方法来解决人脸识别问题，它不包含特征提取和分类器选择阶段，相反它尝试用测试样本表示为训练集的稀疏线性组合。术语“训练样本的稀疏线性组合”意味着如果测试样本可表示为所有训练样本的线性组合，那么大部分成分的组合都是零[6]。如此看来，稀疏表示法试图寻求不同训练样本在“构建”测试样本时潜在的影响，并打算将测试样本分类，它的训练样本具有最大的效果。换句话说，这种方法假定，测试样本可使用不同类的训练样本效果的总和近似表示，并且具有最大效果的类与测试样本最相似[7-8]。

本文提出了一个简单并且快速的人脸识别方法，该方法与稀疏表示法部分相似，然而它在计算上却更加有效，并且有一个独特的特征，其解决方案可以很容易地实现。首先，所提方法从每个类中为每个测试样本，只选择一个邻居样本，然后把测试样本表示为所有选定邻居样本的线性组合，最后，基于表达式结果，该方法构造一个分类过程。所提方法在人脸识别应用中表现出了很好的性能。

由于所提方法仅使用了L个训练样本来表示及分类测试样本(L是所有的类的数目)，也是一种稀疏表示法，且能够继承该方法的优点。分析表明，使用本文方法来选择及使用训练样本是最合适的，因为可产生最小的分类错误。也就是说，如果使用其他L个训练样本来表示和分类测试样本，将获得更高的分类错误。实验结果表明，本文方法比最近邻方法(Nearest Neighbor Classication Methods，NNCM)更好。最近邻方法的确是一种特殊形式的K近邻分类器[9]，最近邻方法首先要确定的是与测试样本最近的训练样本，然后把测试样本分到训练样本的类中。本文的方法由欧氏度量决定，通过修改测试样本和训练样本之间的邻居关系，以达到更好的性能。而且，虽然本文方法执行分类时，依赖的训练样本比NFS[10]方法少得多，但它能获得更好的性能。

1 算法设计及分析

1.1 基于表示的简单快速方法

本节开始描述了所提的基于表示的简单快速方法(Simple and Fast Face Recognition，RSF)，该方法包含两个步骤:第一步，从每个类中选择与测试样本最近的训练样本。假设有L个类，先获得测试样本的L个最近的训练样本(NTS)，每个都各来自一个类;第二步，把测试样本表示为所有选择的L个NTSs的线性组合，并利用所确定的线性组合来对测试样本分类。此外，假设每个训练样本和测试样本均为列向量。

RSF的第二步工作为:假设测试样本y可近似表示为所有NTSk，k=1，2，…，L的线性组合，即假定下面的等式满足

式(2)可改写成

式中:β=(β1，β2，…，βL)T。如果STS是非奇异的，则可以用β=(STS)-1STY来得到式(3)的最小二乘解。如果STS几乎奇异，则利用β=(STS+μⅠ)-1STY来求解β，其中μ是一个正常量，Ⅰ是标识。利用这个方法作为RSF的正规化解决方案。得到β之后，再利用表示Sβ，即=Sβ，为RSF的表达式结果。

等式(2)表明，每个NTS对表示测试样本有着自己的贡献，第i个NTS做的贡献为βiNTSi。此外，第i个NTS表示的测试样本的能力可由βiNTSi与Y之间的偏差来评估。把偏差定义为ei=‖Y-βiNTSi‖2。RSF认为，ei越小，第i个NTS表示测试样本的能力就越强。第二步标识了NTS，其在测试样本中具有最小偏差，并把测试样本分到标识的NTS的类中。应当指出的是，每个类只有一个NTS和第i个NTS对应的第i个类。如果et=minei，那么，测试样本被分到第t类中，参考第t类的最近邻，可以把它当作是RSF所确定的最近邻。

1.2 RSF分析

RSF方法与稀疏表示法[2]不同，它有一个非常简单的解决方案，然而，稀疏表示法的迭代解决方案计算不是很高效;此外，RSF方法可以看作是一种特殊的稀疏表示法。其实，如果RSF中的线性组合强制改写为所有训练样本的线性组合，那么，除了NTS，所有训练样本的线性组合的系数都应该为零。

虽然RSF和文献[2]中的方法都为稀疏表示法，但是它们使用了两种不同的方式来得到稀疏性。RSF使用第一步来产生稀疏性，系数很稀疏(即有多少零系数)，且它的系数均为零。然而稀疏表示法通过迭代算法得到稀疏性，并不知道线性组合的哪些系数等于或近似等0。把所以，也可以把RSF方法称作“硬”稀疏表示法，文献[2]中的方法称为“软”稀疏表示法。

RSF方法有两个优势。第一，它仅利用较少数目的训练样本来表示和分类测试样本。其结果是，RSF方法可以有效地解决式(3)中的计算，当解决式(3)中的线性系统时，它需要的时间复杂度为O(L2M+L3+LM)，其中，M是样本向量的维数。NFS方法解决线性系统，所需要的时间复杂度为O(n2M+n3+nM)=O(nNM+Nn2+NM)，其中，n和N分别是每个类训练样本的数目和所有训练样本的数目。RSF的第二个好处是，虽然简单并且与NNCM部分相似，但是，它比NNCM的性能更好，NNCM可以描述成这样一种方法，它利用每个类的最近邻来对测试样本进行分类。NNCM过程如下:首先，NNCM从每个类中为测试样本选择最近邻。NNCM标识的样本是，在L个选择的最近邻(NTS)中与测试样本最近的那个，并且假设测试样本来自于同一个类中，L是所有类的数目。RSF优于NNCM的主要原因是修改了由欧氏度量决定的测试样本和训练样本之间的邻居关系。如第1.1节所述，在RSF方法中的测试样本与训练样本之间的邻居关系，最终由测试样本与表示NTS测试样本的贡献之间的偏差决定。

RSF的过程如下:第一步，使用欧氏度量来为测试样本从每个类中选择邻居样本;第二步，使用在前面定义的偏差来对测试样本和邻居样本之间的邻居关系重新排序，其中邻居样本由第一步决定。即第二步使用的测试样本与表示NTS测试样本的贡献之间的偏差作为度量标准。第二步使用了这个度量，决定了“最后的近邻”，并且把测试样本分到“最后的近邻”属于的类中。图1显示了所提出的RSF方法的流程图，从图1可以清楚地看到，RSF方法标识的RTS具有最小偏差，假定测试样本来自RTS标识的类中，则RSF方法中的分类等价于基于偏差度量的最近邻分类。

图1 RSF方法的流程图

当RSF尝试使用L个训练样本来表示测试样本时，它需要使用最合适并且最重要的L个样本。即在所有训练样本中，就表示测试样本的能力而言，L个最近邻(NTSs)是最重要的L个训练样本。但其实，如果使用其他的L个样本来表示和对测试样本进行分类，分类的性能可能会很差。

2 算法验证

2.1 人脸库

实验使用了ORL和Yale两大通用人脸数据库来测试所提出的RSF方法。所有的实验均在4 Gbyte内存的Intel Core 2.93 GHz Windows XP计算机上完成，编程环境为MATLAB 7.0。ORL数据库包含40个人的400张人脸图像，每人10张，包含不同的面部表情的变化(笑/不笑，睁/闭眼)和面部细节。对象处于直立正面的位置且具有高达200的倾斜和旋转，每张人脸图像为112×92像素，图2为ORL上某人的10张不同的人脸图像。

图2 ORL上某人的10张人脸图像

Yale数据库包含15个人的165张人脸图像，每人11张，具有许多表情，如正常的、悲伤的、快乐的、困乏的、惊讶的、眨眼的等，且都是在不同的光照条件下获得的，还有一些人脸是带着眼镜的，Yale上某人的11张人脸图像如图3所示。

图3 Yale上某人的11张人脸图像

2.2 实验结果及其分析

为了更好地体现出所提方法的优越性，将所提方法与NNCM[9]、NFS[10]、最远邻方法[4]、使用第一个样本方法[6]、使用最后一个样本方法[6]的错误分类率进行了对比。而且，对于测试样本，通过为每个测试样本选择每个类的第一个或最后一个训练样本，来修改RSF方法，通过选择的第一个或最后一个训练样本来表示和分类测试样本。前面提到的使用了第一个和最后一个训练样本的方法，分别可视为使用第一个样本的方法和使用最后一个样本的方法。从每个类中对测试样本选择最远的邻居来修改所提的RSF方法，利用它们来表示和分类测试样本，引用此方法是因为该方法使用了最远的邻居。

实验选用了ORL及Yale的前l(l=1，2，3，4)张图像作为训练样本，剩下的图像作为测试样本。实现所有的方法之前，先把每个样本向量转换成长度为1的单位向量。使用正则法来获得RSF的解决办法，并设置μ为0.01。参考各方法的所在文献，为各个方法设置不同的参数，进行了大量的实验，并取最佳的实验结果，如表1、表2所示。

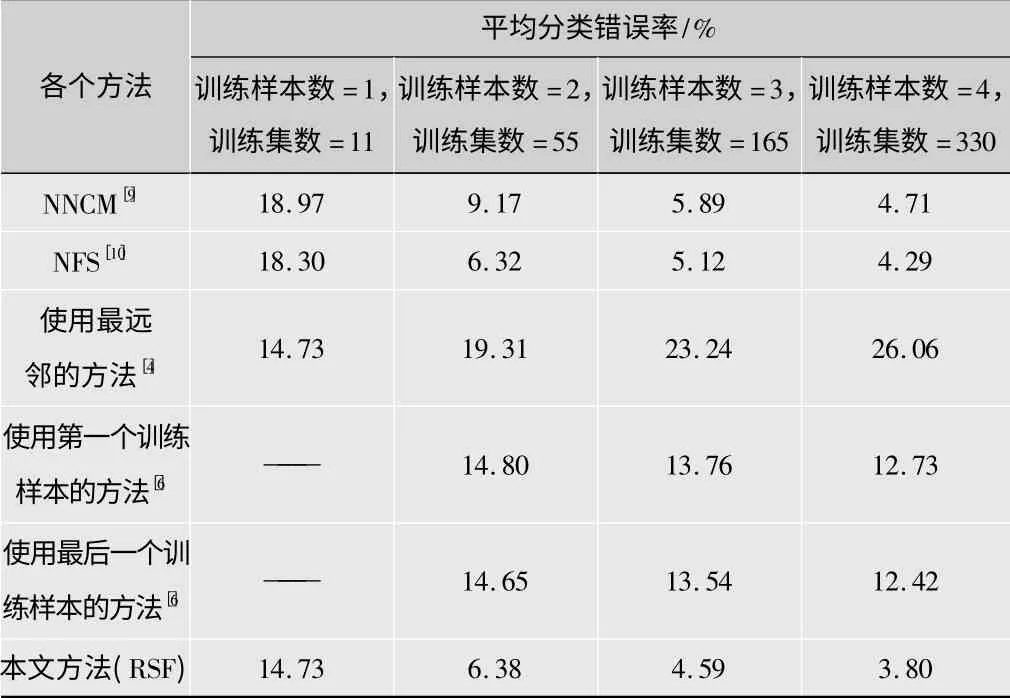
表1 各方法在Yale上的平均分类错误率

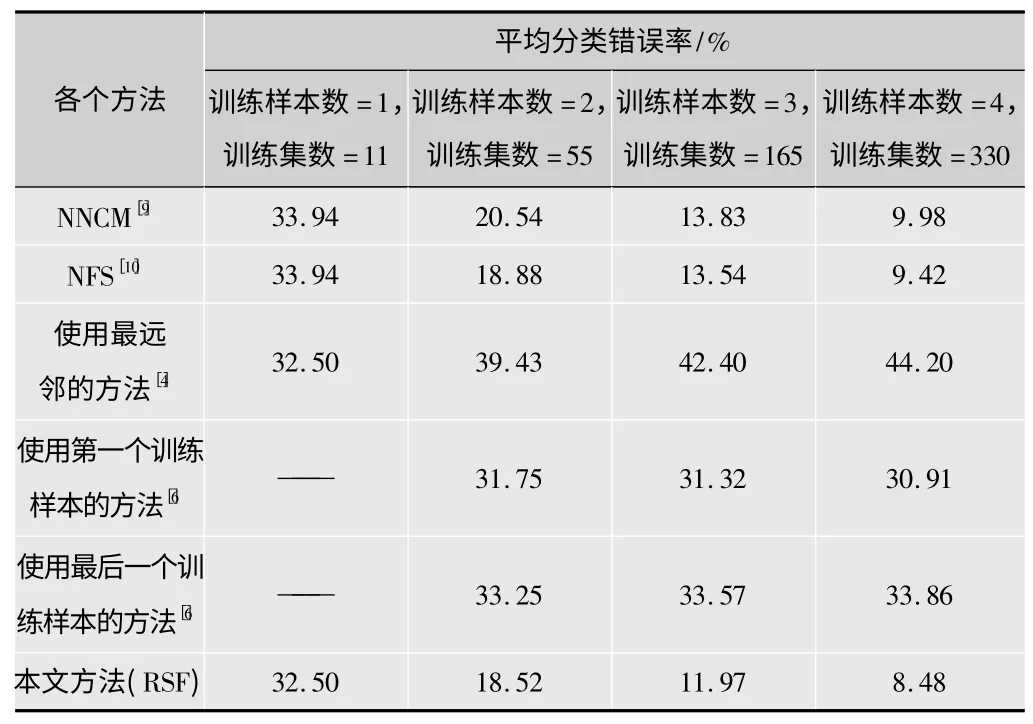
表2 各方法在ORL上的平均分类错误率

从表1、表2可以看出，所提的RSF方法比NNCM、NFS、最远邻的方法、使用第一个样本方法、使用最后一个样本方法分类都精确。RSF的错误率比NNCM、RSF、最远邻方法、使用第一个样本方法、使用最后一个样本方法分别低了0.91%，0.49%，22.26%，8.93%，9.62%。

ORL数据库中RSF的错误率比NNCM、RSF、最远邻方法、使用第一个样本方法、使用最后一个样本方法分别低了1.50%，0.74%，35.72%，22.43%，25.38%。虽然这些方法都使用相同数目的训练样本来表达和分类测试样本，但是RSF使用了最适合的训练样本，所以，无论是在ORL还是Yale数据库，也无论训练样本数为多少，RSF的分类性能总是比其他各个方法更优。

RSF通过利用抑制训练样本中的测试样本的能力，而不仅仅是一个简单的距离来分类测试样本，已被验证是一个用来产生较高分类精度的好方法。分析表明，对于RSF方法，使用的L个最近邻是最合适的训练样本，用其表示和分类测试样本。而且，尽管RSF比NFS方法要更稀疏，但它可能会获得更好的性能。

3 小结

本文提出了一种基于表示的简单快速的人脸识别方法(RSF)，使用了每个类中的最近邻来表示测试样本并对其进行分类。RSF方法比NNCM获得更低的错误率，这两种方法之间准确度的最大差值可能大于10%。除了方法设计和实验分析，本文也直观地描述了RSF的基本原理和特点。

[1]廖海斌，郝宁波，陈庆虎.基于奇异值与稀疏表示的稳健性人脸识别[J].计算机科学，2010，34(7):99-103.

[2]苏煜，山世光，陈熙霖，等.基于全局和局部特征集成的人脸识别[J].软件学报，2010，21(8):1849-1862.

[3]朱杰，杨万扣，唐振民.基于字典学习的核稀疏表示人脸识别方法[J].模式识别与人工智能，2012，25(5):859-864.

[4]柴智，刘正光.应用复小波和独立成分分析的人脸识别[J].计算机应用，2010，30(7):1863-1866.

[5]严慧，金忠，杨静宇.非负二维主成分分析及在人脸识别中的应用[J].模式识别与人工智能，2009，22(6):809-814.

[6]周春光，孙明芳，王甦菁，等.基于稀疏张量的人脸图像特征提取[J].吉林大学学报:工学版，2012，42(6):1521-1526.

[7]崔鹏，张汝波.半监督系数选择法的人脸识别[J].哈尔滨工程大学学报，2012，33(7):855-861.

[8]苏超，肖南峰.基于集成BP网络的人脸识别研究[J].计算机应用研究，2012，29(11):4334-4337.

[9]张强，戚春，蔡云泽.基于判别改进局部切空间排列特征融合的人脸识别方法[J].电子与信息学报，2012，34(10):2396-2401.

[10]王娜，李霞，刘国胜.基于特征子空间邻域的局部保持流形学习算法[J].计算机应用研究，2012，29(4):1318-1321.