窄带Rayleigh快衰落信道中改进的MMSE-SIC检测算法
蔡 黎,代妮娜,戴闽鲁,2
(1.重庆三峡学院 信息与信号处理重点实验室,重庆404000;2.数字电视国家工程实验室(北京),北京101000)
责任编辑:薛 京
在无线通信系统,如CMMB(China Mobile Multimedia Broadcasting,中国移动多媒体广播)系统中,无线信号需要在建筑物密集的城市环境中传播,传输过程中信号会受到电离层和对流层反射的影响。窄带Rayleigh快衰落信道假设信号通过无线信道之后,信号幅度随机,即“衰落”,且其包络服从瑞利分布,因此其通常在理论研究中被作为城市传播环境的统计模型。
窄带Rayleigh快衰落信道模型的广泛应用使得针对它的无线信号检测算法研究越来越成为热点,常见的有ZF(Zero Forcing,迫零)、MMSE(Minimum Mean-Square Error,最小均方误差)、ZF-SIC(Zero Forcing-Serial Interference Cancellation,迫零-串行干扰消除)和MMSE-SIC(Minimum Mean-Square Error-Serial Interference Cancellation,最小均方误差-串行干扰消除)算法,已有文献表明MMSE-SIC在上述算法中表现最优[1]。
实际应用中MMSE-SIC算法存在大量伪逆运算导致检测复杂度增加[2]、恶劣情况下品质恶化情况严重、误码率较高等缺点,因此本文提出一种改进的MMSE-SIC算法。
1 常规MMSE-SIC算法
1.1 算法原理
常规MMSE-SIC算法检测采用贝尔实验室提出的V-Blast(Vertical-BLAST,垂直Blast)模型,模型中天线与层直接对应,即编码后的第k个子流直接送到第k根天线,数据流与天线之间的对应关系无周期改变。因此在检测过程中,只要知道数据来自哪根天线即可判断其来源于哪层,检测过程非常简单。
设窄带Rayleigh快衰落信道模型是空间复用MIMO系统,系统中有NR根发射天线,NT根接收天线(NR≥NT),无线信道呈漫散射和准静态平坦衰落,每根发射天线与接收天线之间经历的衰落相互独立,且接收机能够进行理想信道估计[3],得到MIMO系统的常规MMSE-SIC检测模型如图1所示。
图1所示系统的常规MMSE-SIC检测算法基本步骤表示如下,初始化令i=1,G1=H+(其中Gi为第i次迭代的生成矩阵,H为校验矩阵),而后循环执行以下矩阵迭代运算:
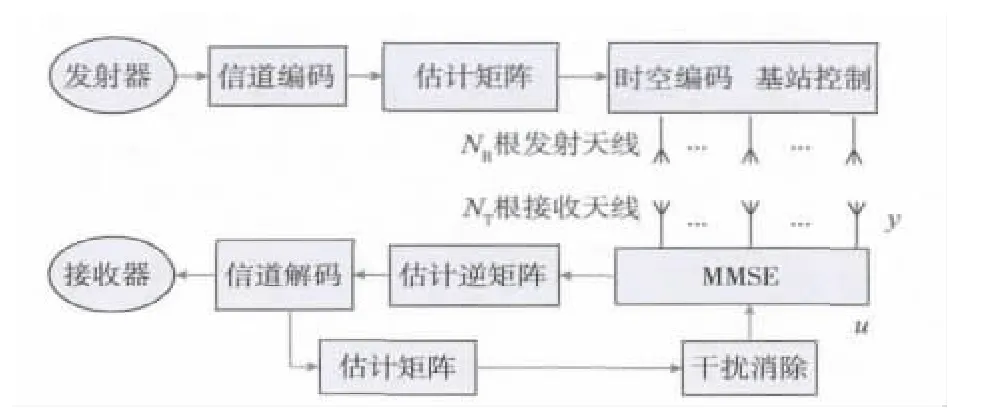
图1 MIMO系统常规MMSE-SIC检测模型

式中:ki表示第k根天线经过第i次迭代;Wki表示第ki根天线生成矩阵;yki表示第ki根天线接收到的信号;ki为经过MMSE检测后的信号;检测信号与校验矩阵hki进行干扰消除得到较好的接收信号ri。
1.2 算法分析
由1.1节的MMSE-SIC原理可知,常规MMSE-SIC检测算法是根据一定的顺序依次检测每层的发射信号,并从接收信号中消除这一层信号造成的干扰,逐次迭代,最后完成对整个信号矢量的检测。因为后检测的信号中干扰已经大大降低,能够获得较好的性能[4-5]。但是这种检测方式需要反复进行排序和矩阵求逆操作,复杂度较高。从1.1中的迭代式可知:MMSE-SIC求解时没有约束,直接得出检测系数矩阵。因此算法的关键在于检测时要进行反复的矩阵求逆运算。
然而在实际通信环境下,随着通信环境恶化导致的系统参数改变,如发射、接收天线增多,信号源数据帧长增加,信噪比范围改变等,都会增加矩阵求逆运算量,从而增加MMSE-SIC算法的复杂度和运算时间,最终降低算法的误比特率。
2 MMSE-SIC算法的改进
2.1 核心思路
1.2 节已分析得:常规MMSE-SIC算法的最大工作量在于检测时需要进行反复的矩阵求逆运算,因此可以思考从反复的矩阵求逆运算中寻求突破。
在此引入广义预测控制矩阵求逆的快速算法,即在通过预测矩阵的存在改进矩阵预算的速度,从而改善整个MMSE-SIC算法的性能,改进核心思路如图2所示。
2.2 快速矩阵和求逆算法
步骤如下:
1)构造模型
考虑如下CARIMA(Autoregressive Integrated Moving Average,差分自回归移动平均)模型

图2 MMSE-SIC算法改进核心流程图

式中:y为系统输入;u为系统输出;ξ(k)为假设的高斯白噪声(均值为0、方差为1);引入的差分算子Δ=1-z-1,且A(z-1)=1+a1z-1+a2z-2+…+anz-n,B(z-1)=1+b1z-1+b2z-2+…+bnz-n,C(z-1)=1+c1z-1+c2z-2+…+cnz-n。
2)引入预测方程
在CARIMA模型中引入Diophantine方程以实现预测,方程中包含由A(z-1)、B(z-1)唯一确定的多项式,预测长度j,Diophantine方程[6]为

3)得到预测矩阵
令N为预测时域,Nu为控制时域(Nu<N),得到系统输出预测矩阵为

U=[Δu(k),Δu(k+1),…,Δu(k+Nu-1)]T;F=[F1(z-1),F2(z-1),…,FN(z-1)]T;H=[H1(z-1),H2(z-1),…,HN(z-1)]T;E=[E1(z-1)ξ(k+1),E2(z-1)ξ(k+2),…,EN(z-1)ξ(k+N)]T;G的表达式为
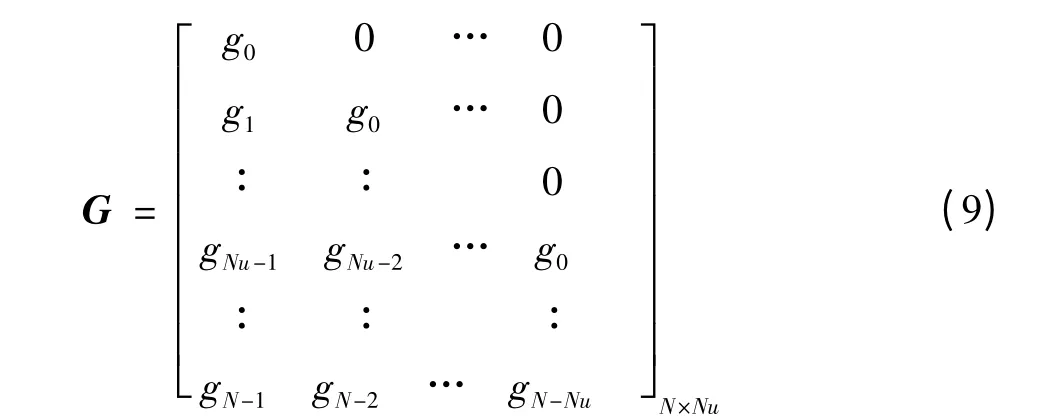
至此,快速矩阵和求逆算法即得。
3 仿真与分析
3.1 仿真结果
选MATLAB7.0为仿真环境,以第2.2节中提出的改进MMSE-SIC算法为仿真对象,传统ZF、ZF-SIC、MMSESIC作为对比仿真对象,设信源A是帧长为2 000的比特流,经BPSK(Binary Phase Shift Keying,二进制相移键控)调制后发射,引入一定强度的高斯白噪声,用M文件建立窄带Rayleigh快衰落信道通信模型[7],构造4种不同的通信环境,以观察不同通信环境下不同检测算法的误比特率表现。
4种通信环境:1)理想通信环境:发射天线数4、接收天线数3,信噪比范围0~20 dB;2)普通通信环境:发射天线数2、接收天线数2,信噪比范围0~20 dB;3)恶劣通信环境:发射天线数2、接收天线数2,信噪比范围0~20 dB;4)极端通信环境发射天线数2、接收天线数2,信噪比范围0~20 dB。
以足够多的数据进行运算,得到仿真结果如图3~图6所示。




3.2 结果分析
从仿真结果图可知,在理想通信环境下,4种算法均有较好的误比特率表现,理想通信环境下4种算法误比特率表现都很好,但改进后的MMSE-SIC的表现最优,误比特率逼近10-4数量级;普通通信环境下,4种算法也均呈较好的误比特率表现,改进后的MMSE-SIC的表现最优,误比特率逼近10-4的数量级;在恶劣通信环境下,4种算法通信品质呈一定恶化,改进后的MMSE-SIC的表现仍然最优,误比特率接近10-2数量级;在极端通信环境下,4种算法通信品质都严重恶化,误码率均徘徊在10-1的数量级上下,改进后的MMSE-SIC的表现仍然相对最优。
4 小结
本文通过引入预测矩阵改善矩阵运算的速度,从而改善了常规MMSE-SIC检测算法的性能,仿真表明改进的MMSE-SIC算法相对于常规MMSE-SIC算法,在各种通信环境下均表现出了较好的误比特率性能,具有较高的参考和应用价值。
[1]黄玉娟.VBLAST系统的译码算法研究[J].通信技术,2011(2):65-68.
[2]张建忠.基于QR分解的V-BLAST检测算法研究[J].电视技术,2010,34(5):89-91.
[3]范忠亮.基于矩阵和求逆及MRC的低复杂度MIMO检测器[J].测控技术,2011(9):98-101.
[4]包亚伟.一种新的高效MMSE-SIC检测算法[J].系统仿真学报,2011(7):1350-1353.
[5]CHEN Jiming,JIN Shan,WANG Yonggang.Reduced complexity MMSESIC detector in V-BLAST systems[C]//Proc.18th Annual IEEE International Symposium on Personal,Indoor and Mobile Radio Communications.Athens:IEEE Press,2007:1-5.
[6]陈志兴.广义预测控制矩阵求逆的快速算法研究[J].科技信息,2012(31):89-90.
[7]邱佳新.V-BLAST程序[EB/OL].[2013-01-10].http://www.pudn.com/downloads254/sourcecode/math/detail1175182.html.

