水库蓄水裂隙岸坡断裂损伤分析
宋维胜,赵延林,李江腾
(1. 张家界市 水利局,湖南 张家界,427000;2. 湖南科技大学 煤矿安全开采技术湖南省重点实验室,湖南 湘潭,411201;3. 中南大学 资源与安全工程学院,湖南 长沙,410083)
水库蓄水裂隙岸坡断裂损伤分析
宋维胜1,赵延林2,李江腾3
(1. 张家界市 水利局,湖南 张家界,427000;2. 湖南科技大学 煤矿安全开采技术湖南省重点实验室,湖南 湘潭,411201;3. 中南大学 资源与安全工程学院,湖南 长沙,410083)
基于能量原理,用初始损伤张量和裂纹扩展附加损伤张量描述裂隙岸坡水−岩作用下的损伤演化过程,得到裂隙岩体在考虑渗透压作用下的本构关系与损伤演化方程,探讨渗透压作用下裂隙损伤效应对渗透张量的影响,建立裂隙岩体渗流场与损伤场耦合的分析模型。在此基础上,以水库蓄水期库区裂隙岸坡为例,进行渗流—损伤—断裂耦合分析。研究结果表明:随着蓄水深度的提高,断层及岸坡损伤范围扩大,相对损伤增加,x方向的渗透系数kxx随着水深增大而不断增大,所得结果可为岸坡的治理提供依据。
裂隙岸坡;渗流场;损伤演化;压剪断裂;水库蓄水
水库滑坡主要是水库蓄水或运营导致岸坡水动力条件不利而演化造成的,包括水位的涨落及暴雨入渗2个方面。中村浩之等[1]经过对水库滑坡分析及其实测认为,浸水、库水位急剧下降和降雨是水库滑坡形成的主要因素。王思敬等[2]将水库滑坡分为 2种:一种是水库在水岩作用影响下的滑坡,另一种是天然滑坡。王士天等[3]认为水库滑坡发生在 2个阶段:一是库水位达到敏感水位后滑体内孔隙水压力分布达到新的平衡过程;二是发生在库水位消落特别是快速消落期。蔡耀军等[4]认为水库诱发岸坡变形与失稳可归结为 3个因素:一是材料力学效应,二是水力学效应,三是水力机械作用。边坡稳定性变化幅度受控于不稳定的几何形状、水文地质条件及潜在破坏面的强度。严福章等[5]通过对清江隔河岩水库茅坪滑坡的研究认为该滑坡在水库蓄水后发生持续的缓慢变形,其根本原因是水库蓄水产生的材料力学效应和水力学效应综合作用的结果,其次是滑体发生变形后,滑带抗剪强度随变形而降低的应变软化作用。然而,水库的蓄水过程是裂隙库岸边坡水岩环境动态变化的过程,Riemer统计了60个水库滑坡实例,指出 85%的滑坡发生在建设或蓄水期或工程完工2 a内[6]。Vajont 近坝库岸岩体大滑坡显示出与土坝滑坡完全不同的规律,土坝滑坡常发生在水位降落时段。每当库水位上升时,Vajont裂隙岩石坡体岸坡位移速率随之增大,而当库水位降低时,位移速度减小。对于库水位上升导致的裂隙岸坡的失稳机制,只有采用流固耦合分析方法,从岩石水力学的角度研究岩体的渗透规律和损伤力学响应才能较真实地揭示地质灾害的本质。为此,本文作者基于能量原理,用初始损伤张量和裂纹扩展附加损伤张量描述裂隙岸坡水−岩作用下的损伤演化过程,建立裂隙岩体在考虑渗透压作用下的本构关系与损伤演化方程,探讨渗透压作用下裂隙损伤效应对渗透张量的影响,建立裂隙岩体渗流场与损伤场耦合的分析模型。以水库蓄水期库区裂隙岸坡为例,分析渗流—损伤—断裂耦合。
1 裂隙岸坡的水−岩作用机理
1.1 水−岩作用下裂隙岩体本构关系
按照Betti 能量互易定理,n组裂隙岩体初始等效损伤张量可表述为[7−9]

其中:i=1, 2, 3; j=1, 2, 3。当岩体分布有任意方向的n组裂隙时,采用坐标变换和叠加原理, 可得压剪应力状态下裂隙变形产生的附加柔度张量为
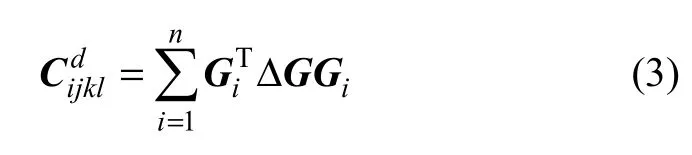
参照文献[10]和[11],对图1(a)所示三维币状剪切滑动裂纹可简化为图1(b)所示二维裂纹来处理。
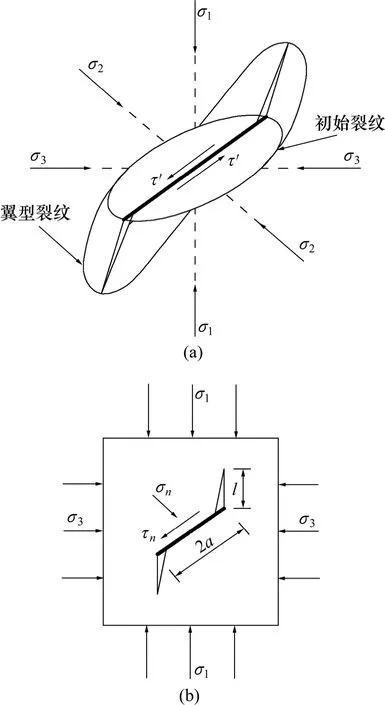
图1 三维币状裂纹扩展简化成平面裂纹扩展示意图Fig.1 Diagram of 3D crack simplified as 2D crack
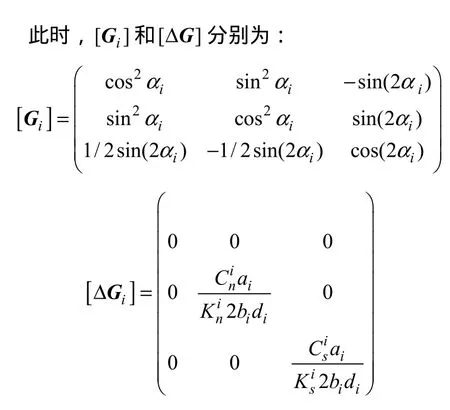
式中:i为第i组裂隙走向与x轴的夹角;和分别第i组裂隙面的传压和传剪系数;和分别为第i组裂隙面的法向和切向刚度;bi为第i组裂隙中心距离之一半;di为第i组裂隙间距之一半;ai第i组裂隙间距之一半。此时,本构方程为

由于裂隙水压力的存在增大了岩体的柔度张量,使得岩体力学特性变弱,由广义虚功定律,假定水流仅在裂隙中流动,岩块本身不导水,初始压剪应力状态在渗透压p作用下裂隙岩体的本构方程为
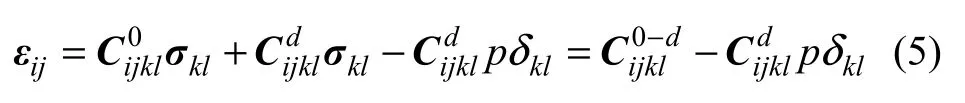
1.2 水−岩作用下裂隙岩体损伤演化
处于压应力占优势的节理岩体,其裂隙随外加载荷的增加而经历闭合摩擦滑动,压剪起裂,形成分支张型裂纹,直至裂纹击穿岩桥,介质互相会合,彼此贯通,使岩体破坏。参照文献[12−14],分支裂纹长度与应力强度因子KI的关系为
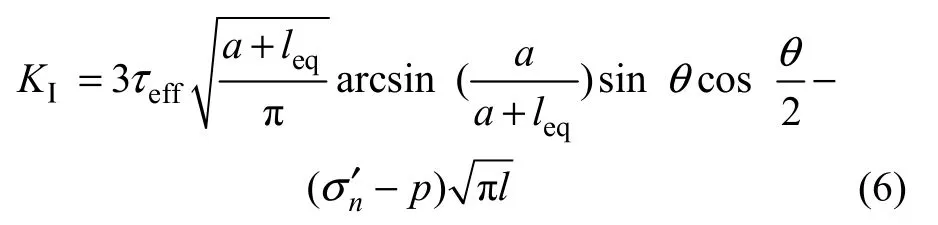


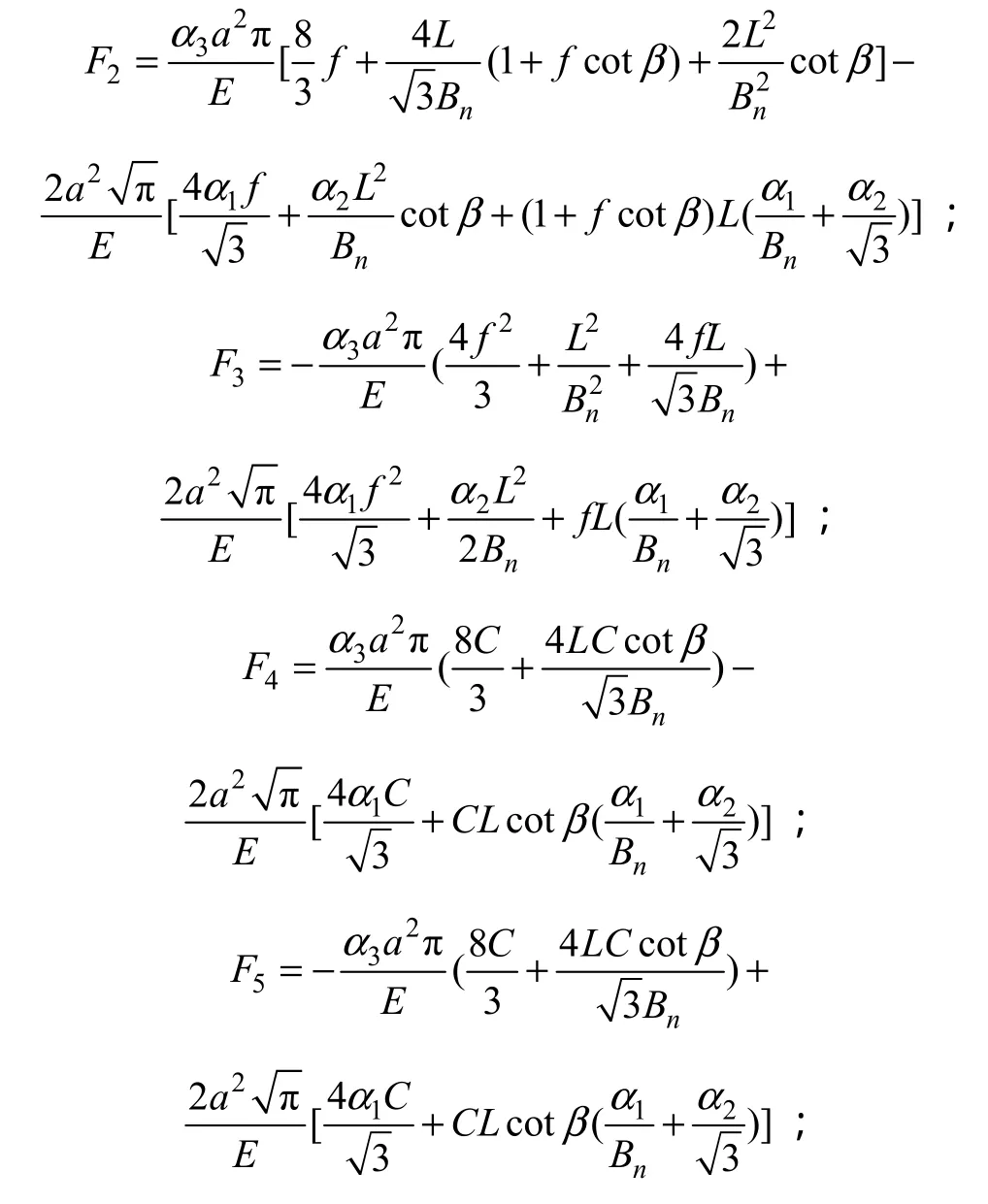
C为裂隙面的黏结力; σ(j)为作用于单元体第j 组裂隙面上的正应力;Φ 为裂隙面的摩擦角;τ(j)为作用于单元体第j 组裂隙面的剪应力;β为单元体最小主应力与裂隙所成的锐角;l为分支裂纹长度:

渗透压作用下裂隙岩体的演化方程为
1.3 损伤效应对渗透张量的影响
裂隙岩体渗透张量的变化依赖于应力状态的改变,随应力状态和渗流状态的改变,原有裂隙的规模及张开度相应变化,甚至会导致岩体裂隙发生劈裂、扩展、连通等损伤行为。随着岩体裂隙损伤断裂的演化,裂隙岩体的渗透张量会发生较大改变。在压剪状态下,裂隙面滑移扩展,在法向应力和渗透压共同作用下,裂隙面法向变形为[14]
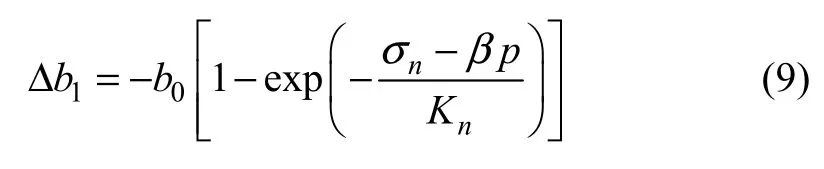
由于翼形分支裂纹的产生而引起的裂隙平均张开度为
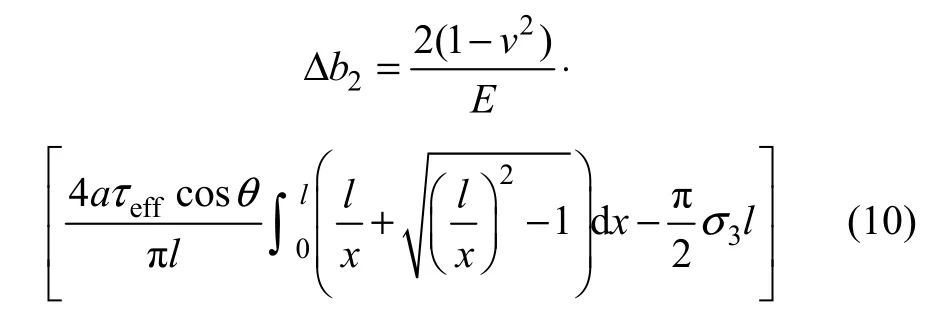
式中: 为裂隙法向与最小主应力3方向的夹角;l为翼形分支裂纹的长度。裂隙面法向总变形为
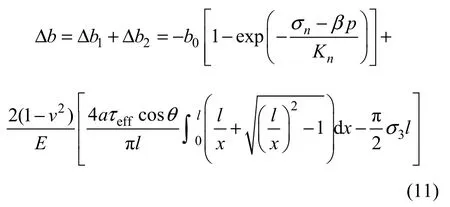
在压剪状态下,裂隙面滑移扩展下渗透张量为

1.4 裂隙岩体渗流—应力—损伤耦合方程
对于各向异性含水层地下水三维不稳定流,拟连续岩体介质非稳态渗流控制方程为[14]

2 算例
某水库岸坡山体构造较发育,上游左岸坡山体发育断层带F1,断层带F1不平直,宽120~200 cm,断层带内断层泥较破碎,断层长约4 km。右岸坡山体发育平直断层带 F2,产状为 293.8°∠32°,断层带宽约100 cm。断层带F1和F2位置分布见图2和图3;岩体发育着二组低序次节理裂隙,其统计方向和产状见表1,计算参数见表2。
根据本文给出的裂隙岩体弹塑性损伤本构方程和渗流方程编制的有限元分析程序,对该岸坡进行有限元分析。图4所示为岸坡及左、右断层相对损伤随水深变化时的关系;图5所示为 x方向的渗透系数 kxx随水深的变化情况。从图4和图5可以看出:随着蓄水水深的增大,相对损伤及x方向的渗透系数kxx都会增大。
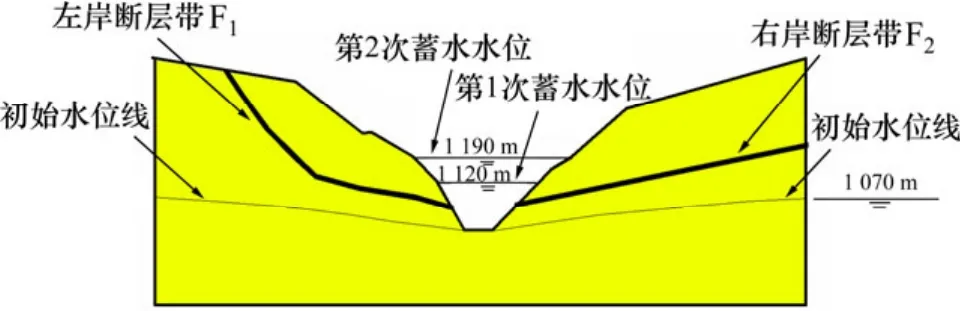
图2 岸坡纵剖面示意图Fig.2 Longitudinal profile of fissured rock slope

图3 裂隙岸坡计算模型Fig.3 Computational model of fissured rock slope
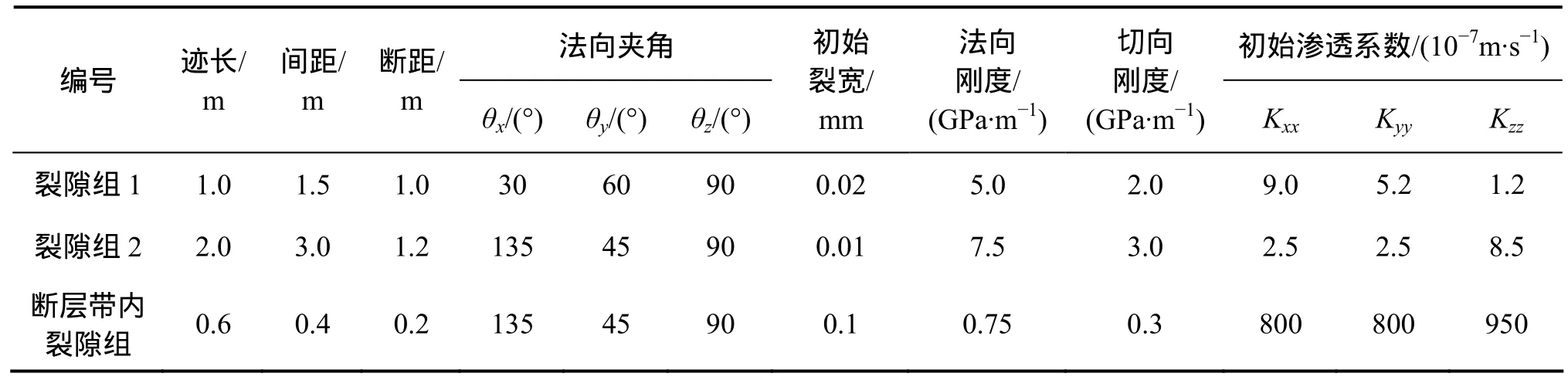
表1 裂隙组几何和力学统计参数Table 1 Geometrical and mechanical parameters of discontinuous crack sets
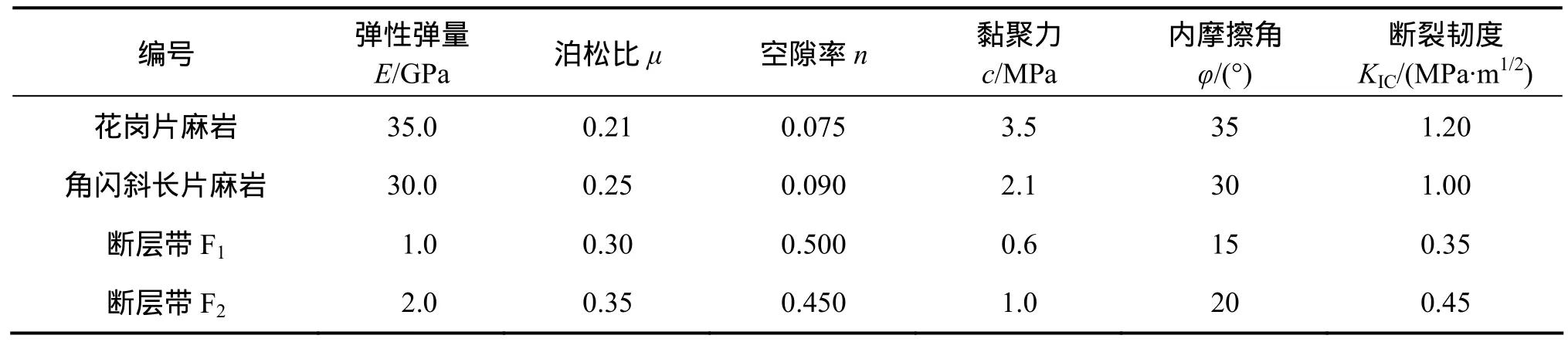
表2 岩体分区计算参数Table 2 Mechanical parameters of rock mass and fault zone
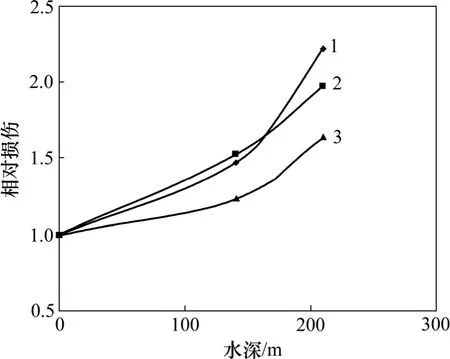
图4 相对损伤与水深的关系Fig.4 Relationship between relative damage and water depth
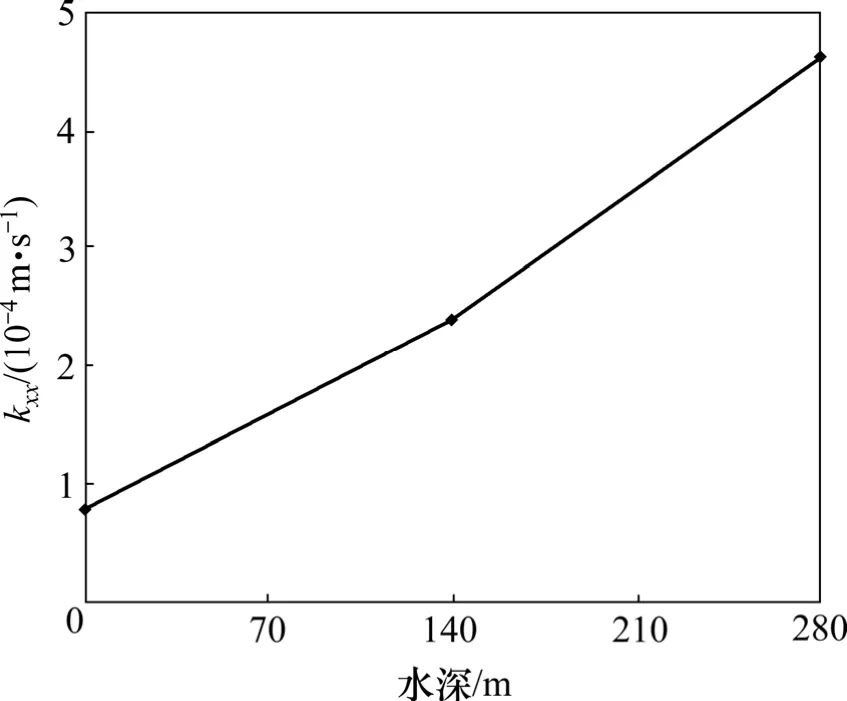
图5 kxx与水深的关系Fig.5 Relationship between kxx and water depth
3 结论
(1) 得到了裂隙岩体在考虑渗透压作用下的本构关系与损伤演化方程,探讨了渗透压作用下裂隙损伤效应对渗透张量的影响,建立了裂隙岩体渗流场与损伤场耦合的分析模型,并将其用于水库蓄水期库区裂隙岸坡分析。
(2) 随着水位上升,断层及岸坡损伤范围扩大,并向岸坡深部扩展;损伤区随水位上升迅速贯通,岩体的抗滑能力进一步降低,这表明水库蓄水后是岸坡失稳的一个诱因。所给出的损伤区为工程加固提供了依据。
(3) 渗透系数随水深增大而增大。本文所建立的损伤流固耦合模型考虑了损伤对渗透张量的影响,更加真实地反映了流固耦合分析过程中岩体渗透系数的变化规律,使得计算结果更加符合实际结果。
[1] 中村浩之, 王恭先. 论水库滑坡[J]. 水土保持通报, 1990,10(1): 53−64.
Nakamura H, WANG Gongxian. Study on land slide in reservoir area[J]. Bulletin of Soil and Water Conservation, 1990, 10(1):53−64.
[2] 王思敬, 马凤山, 杜永廉. 水库地区的水岩作用及其地质环境影响[J]. 工程地质学报, 1996, 4(3): 1−9.
WANG Sijing, MA Fengshan, DU Yonglian. On the rock-water interaction in reservoir areas and its geoenvironmental effect[J].Journal of Engineering Geology, 1996, 4(3): 1−9.
[3] 王士天, 刘汉超, 张悼元, 等. 大型水域水岩相互作用及其环境效应研究[J]. 地质灾害与环境保护, 1997, 8(1): 69−89.
WANG Shitian, LIU Hanchao, ZHANG Zhuoyuan, et al.Research on the water rock interaction and its environmental effects in reservoir areas[J]. Journal of Geological Hazards and Enveronment Preservation, 1997, 8(1): 69−89.
[4] 蔡耀军, 郭麒麟, 余永志. 水库诱发岸坡失稳的机制及其预测[J]. 湖北地矿, 2002, 16(4): 4−8.
CAI Yaojun, GUO Qilin, YU Yongzhi. The reservoir-induced slope failure mechanism and prediction[J]. Hubei Geology &Mineral Resources, 2002, 16(4): 4−8.
[5] 严福章, 王思敬, 徐瑞春. 清江隔河岩水库蓄水后茅坪滑坡的变形机理及其发展趋势研究[J]. 工程地质学报, 2003, 11(1):15−24.
YAN Fuzhang, WANG Sijing, XU Ruichun. Deformation mechanism and development tendency of Maoping landslide after impounding of geheyan reservoir on qingjiang river, hubei province,china[J]. Journal of Engineering Geology, 2003, 11(1):15−24.
[6] 张有天. 岩石水力学与工程[M]. 中国水利水电出版社, 2005:14−20.
ZHANG Youtian. Rock hydraulics and engineering[M]. China Water Power Press, 2005: 14−20.
[7] 赵延林, 曹平, 赵阳升, 等. 双重介质渗流场−应力场−温度场耦合模型及三维数值研究[J]. 岩石力学与工程学报, 2007,26(增刊 2): 4024−4031.
ZHAO Yanlin, CAO Ping, ZHAO Yangsheng, et al. Dual media model for thermo–hydro–mechanical coupling and 3D numerical simulation[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S2): 4024−4031.
[8] 朱珍德, 徐卫亚. 裂隙岩体渗流场与损伤场耦合模型研究[J].河海大学学报: 自然科学版, 2003, 31(2): 155−159.
ZHU Zhende, XU Weiya. Theoretical study on a coupled seepage damage model for fissured rock masses[J]. Journal of Hohai University: Natural Sciences, 2003, 31(2): 155−159.
[9] 易顺民, 朱珍德. 裂隙岩体损伤力学导论[M]. 北京: 科学出版社, 2005: 8−10.
YI Shunmin, ZHU Zhende. Damage theory introduction of fractured rock mass[M]. Beijing: Science Press, 2005: 8−10.
[10] 朱维申, 张强勇. 节理岩体脆弹性断裂损伤模型及其工程应用[J]. 岩石力学与工程学报, 1999, 18(3): 245−249.
ZHU Weishen, ZHANG Qiangyong. Brittle elastic fracture damage constitutive model of jointed rockmass and its application to engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(3): 245−249.
[11] 杨延毅. 节理裂隙岩体损伤断裂力学模型及其在岩体工程中的应用[D]. 北京: 清华大学水利水电工程系, 1990: 46−73.
YANG Yanyi. Fracture damage model for jointed rock mass and its application to the rock engineering[D]. Beijing: Tsinghua University. Department of Hydraulic Engineering, 1990: 46−73.
[12] Kemeny J M. A model for nonlinear rock deformation under compression due to subcritical crack growth[J]. Int J Rock Mech Min Sci, 1991, 28(2): 459−467.
[13] Kemeny J M, Cook N G W. Crack models for the failure of rocks in compression, constitutive laws for engineering materials[C]//Theory and Applications. New York: Elsevier,1987: 879−887.
[14] 赵延林. 裂隙岩体渗流—损伤—断裂耦合理论及应用研究[D].长沙: 中南大学资源与安全工程学院, 2009: 26−49.
ZHAO Yanlin. Coupling theory of seepage-damage-fracture in fractured rock masses and its application[D]. Changsha: Central South University. School of Resources and Safety Engineering,2009: 26−49.
[15] 郑少河, 朱维申. 裂隙岩体渗流损伤耦合模型的理论分析[J].岩石力学与工程学报, 2001, 20(2): 156−159.
ZHENG Shaohe, ZHU Weishen. Theoretical analysis on a coupled seepage-damage model of fractured rock mass[J].Chinese Journal of Rock Mechanics and Engineering, 2001,20(2): 156−159.
[16] 郑少河. 裂隙岩体渗流场-损伤场耦合理论研究及工程应用[D]. 武汉: 中国科学院武汉岩土力学研究所, 2000: 28−43.
ZHENG Shaohe. Research on coupling theory between seepage and damage of fractured rock mass and its application to engineering[D]. Wuhan: Chinese Academy of Sciences. Institute of Rock and Soil Mechanics, 2000: 28−43.
[17] 朱珍德, 胡定. 渗流损伤耦合模型在三峡工程中的初步应用[J]. 武汉水利电力大学(宜昌)学报, 1999, 21(1): 1−6.
ZHU Zhende, HU Ding. Primary application of the coupling model of seepage and damage on the three gorges project[J].Journal of University of Hydraulic and Electric Engineering(Yichang), 1999, 21(1): 1−6.
(编辑 陈灿华)
Fracture damage analysis of fissured rock slope at reservoir storage
SONG Weisheng1, ZHAO Yanlin2, LI Jiangteng3
(1. Zhangjiajie Water Conservancy Bureau, Zhangjiajie 427000, China;2. Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines,Hunan University of Science and Technology, Xiangtan 411201, China;3. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
According to the energy principle, the damage evolution process was described by initial damage tensor and crack propagation additional damage tensor under water-rock in fracture slope. The constitutive relation and the damage evolution equation was obtained during the action of osmotic pressure in fractured rock mass. The effect of crack damage on permeability tensor was discussed. The coupling model was established about the seepage field and the fractured rock mass damage field. Taking a fissured rock slope at reservoir storage as an sample, the coupling model about seepagedamage-fracture was analyzed. The calculation results show that the damage zone of fault and slope increases with the increase of the storage water level enhancement, and relative damage increases too. The permeability coefficient kxxin x direction increases with the increase of the water depth, which can provide basis for slope reinforcement.
fissured rock slope; seepage field; damage evolution; shear fracture; reservoir storage
TV223.1
A
1672−7207(2013)03−1197−06
2012−04−02;
2012−07−20
国家自然科学基金资助项目(51274097);湖南省水利厅科技项目(2010)
宋维胜(1966−),男,湖南张家界人,高级工程师,从事水利工程的设计与管理工作;电话:13787440525;E-mail: swsh1010@sina.com

