单框架控制力矩陀螺复合操纵律设计
吴忠 邓世龙 魏孔明 郭雷
(北京航空航天大学仪器科学与光电工程学院,北京 100191)
1 引言
单框架控制力矩陀螺(SGCMG)是应用在航天器上的一类惯性执行机构,通过动量交换产生内部力矩,对航天器进行姿态控制[1]。为操纵SGCMG 系统产生姿态控制所需的期望控制力矩,必须设计高性能的SGCMG 操纵律。
SGCMG 操纵律通常采用Jacobi阵的伪逆,算法形式简单,易于实现。然而,正是由于Jacobi阵伪逆的应用,使得Jacobi阵一旦奇异时,其伪逆不定,从而导致算法失败[1]。虽然可以加入零运动(如梯度型零运动)来回避系统奇异,但该算法本质上仍然是一种局域的切空间方法,不能保证奇异回避的全局性,易陷入内部椭圆奇异。
与伪逆操纵律不同,奇异鲁棒(SR)逆操纵律通过引入一定的操纵误差,在Jacobi阵奇异时仍能输出可行的框架角速率,但对内部椭圆奇异,仍无能为力[1]。为此,人们先后提出了多种改进的奇异鲁棒逆操纵律,如非对角奇异鲁棒(o-DSR)逆操纵律、奇异方向回避(SDA)操纵律、改进的SDA 操纵律、混合逆操纵律、预报奇异鲁棒逆操纵律、基于反馈的操纵律、带零运动的SDA 操纵律以及奇异曲面回避操纵律等[1-4]。然而,改进的奇异鲁棒逆操纵律本质上仍然是通过引入操纵误差来逃离奇异,不能为姿态控制提供精确控制力矩。
为兼顾操纵律精度及奇异回避和逃逸性能,文献[5]将Radical Basis Function(RBF)神经网络引入SGCMG 操纵律的设计,可以较小的框架角速度穿越系统的奇异状态。文献[6]根据期望的角动量轨迹,全局搜索框架角空间中的最优路径。文献[7]则引入模糊决策方法,改善操纵律的奇异回避性能。以上操纵律大都可以兼顾操纵律的精度及奇异回避性能,但计算较为复杂。
为降低计算负担,借鉴机器人领域中逆运动学求解的动态方法,文献[8]设计了一种SGCMG动态操纵律。该操纵律不用计算Jacobi阵的伪逆,而是代之以Jacobi阵的转置,从而避免了由Jacobi阵求伪逆带来的一系列问题。同时,该操纵律形式简单,易于实现。虽然该操纵律可通过牺牲一定的操纵精度回避或逃逸内部双曲型奇点,但对于内部椭圆型奇点却无能为力。
为进一步改善动态操纵律的奇异回避和逃逸性能,受复合控制的启发,本文在动态操纵律中,引入可以辅助奇异回避和逃逸的前馈信息,设计了一种基于前馈和反馈两种信息的复合操纵律。当SGCMG 系统接近或陷入奇异时,在动态操纵律的基础上引入前馈信息,辅助SGCMG 系统回避或逃逸奇异。
2 SGCMG 系统运动学及问题描述
2.1 SGCMG 系统运动学
为便于讨论,设待研究的SGCMG系统是冗余的,且n个SGCMG是相同的。设σi、hi和ji分别表示第i个SGCMG 的框架角、角动量矢量和输出力矩矢量,则SGCMG 系统的总角动量可以表示为
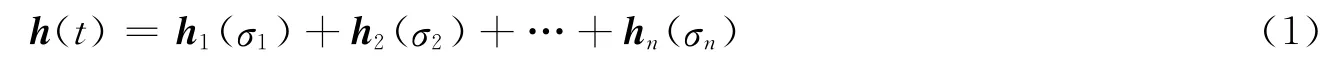
如令σ=[σ1,σ2,...,σn]T,并采用非线性矢量函数f(·)表示SGCMG 系统的运动学关系,则式(1)可写为[8]

在不考虑载体运动的情况下,对式(2)两端微分,可以得到:
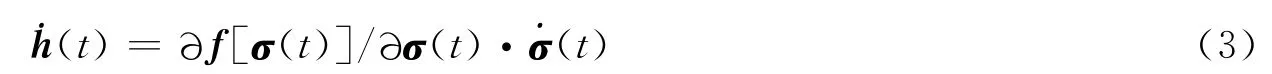
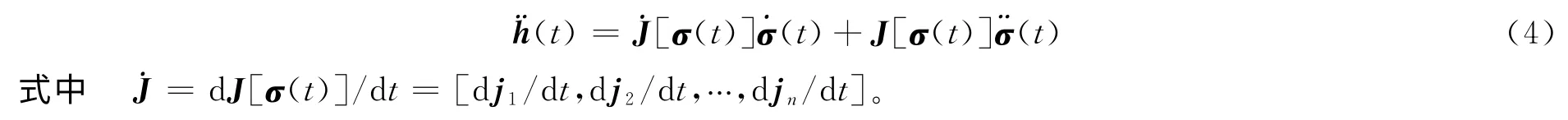
2.2 操纵律设计问题描述
SGCMG 系统操纵律的设计问题是一个典型的控制分配问题,主要任务是把航天器姿态控制所需的力矩指令(或角动量指令)分解为每个SGCMG 的框架指令。假设期望角动量指令为hd(t),存在并有界,操纵律的任务就是根据SGCMG 系统的运动学关系式(1)~式(3),找到可行的SGCMG 系统框架角指令σ(t)或框架角速度指令(t),使得SGCMG 系统的角动量h(t)逼近角动量指令hd(t),或使得SGCMG 系统的力矩逼近力矩指令(t)。
3 SGCMG 系统复合操纵律设计
3.1 复合操纵律的基本结构
为在操纵律中避免Jacobi阵伪逆的求解,文献[8]借鉴机器人领域的研究成果,设计了一种SGCMG 动态操纵律。由于动态操纵律只需计算Jacobi阵的转置,不仅计算量小,而且避免了由Jacobi阵求伪逆带来的一系列问题。对于一般的双曲型奇点,动态操纵律可通过牺牲一定的操纵精度进行回避或逃逸。一旦遇到内部椭圆型奇点,SGCMG 系统往往会出现“框架死锁”现象,不能逃逸。
考虑到动态操纵律是一种闭环结构的反馈算法,受复合控制的启发,在此可引入包含SGCMG系统非奇异路径信息的前馈环节,组成“反馈+前馈”的复合操纵律,以在接近或陷入奇异时回避或逃逸奇异。根据以上思路,可设计复合操纵律的结构如图1所示。复合操纵律由两部分组成,一部分为基于反馈的动态操纵律,输出为(t);另一部分为基于前馈的补偿器,输出为(t)。将两部分的输出相加,即可得到复合操纵律的输出指令。
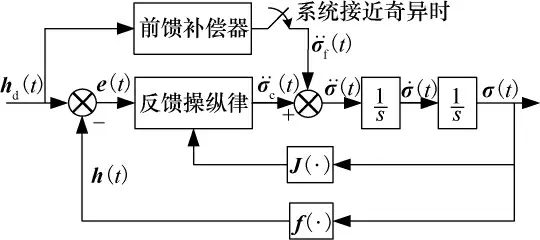
图1 SGCMG 复合操纵律的基本结构Fig.1 Structure of the hybrid steering law for SGCMGs
根据前馈的实质,前馈补偿器应为SGCMG 系统运动学及二次积分环节的逆,前馈信号f(t)经两次积分后应满足:
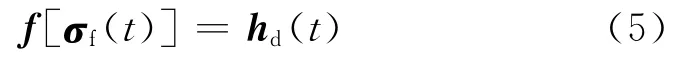
3.2 反馈操纵律
反馈操纵律采用文献[8]中设计的动态操纵律。参照文献[8],直接给出动态操纵律的输出信号如下:


需要说明的是,参数α和β 的选取主要考虑动态操纵律的收敛过程,而参数γ1和γ2的选取除参考式(7)外,可采用简单易行的工程整定法,并考虑框架伺服电机所允许的最大框架角加速度。然而,一旦系统奇异,满足式(7)的γ2将不存在。当γ2取指定的值时,动态操纵律依然可以工作,此时操纵误差将变大。
与普通的奇异鲁棒逆操纵律相似,当系统遭遇双曲型奇点时,动态操纵律可通过一定的操纵误差回避或逃离奇点。当系统遭遇椭圆型奇点时,动态操纵律将陷在奇点处,无法逃逸。
3.3 前馈补偿器
对应一个特定的姿态机动过程,期望的角动量轨迹一般是已知的。此时,可以利用框架角运动的先验信息作为前馈信号。先验信息可以采用离线非线性规划方法,通过大量的数值运算获得。在没有先验信息的情况下,只能对前馈信号进行构造。前馈信号构造的原则是确保SGCMG 系统不奇异,但σf(t)可能不严格满足式(5),而是产生一定的操纵误差。由前馈信号产生的误差会进入图1所示的反馈通道,由反馈加以适当抑制。也就是说,采用“反馈+前馈”的复合操纵律,既可以通过前馈回避或逃逸奇异,又可以通过反馈对操纵误差进行抑制,优势互补。
为构造前馈信号,对于一个特定的姿态机动过程,可定义一个期望的SGCMG 系统框架角。在前馈信号作用下,可使SGCMG 系统始终以最快速度转向期望框架角,不受奇异状态的影响。对于SGCMG 系统而言,在期望的力矩指令下,其角动量矢量将沿着力矩方向运动,直到到达角动量包络,出现饱和奇异。实际上,前馈信号构造的目的就是在SGCMG 系统到达饱和奇异前,回避或逃逸内部奇异。因此,可把饱和奇异对应的饱和框架角作为期望框架角[9],并依此来构造前馈信号。
为方便起见,前馈信号的构造基于离散域进行。设采样周期为T,在t=kT 时刻,如果期望力矩的方向为,第i个SGCMG的角动量方向为力矩方向为,则饱和框架角与当前框架角的距离为

进而可以得到:

那么,对于第i个SGCMG 而言,前馈信号可以构造为

式中 1≥γ3>0为适当选取的前馈系数。注意到框架角的周期性,在对式(8)、式(9)进行计算时,把Δσi(k)、∇σi(k)的取值范围统一化成[-π,π],以保证框架角的变化是最短路径。由此,可以得到k 时刻SGCMG 系统的前馈信号为
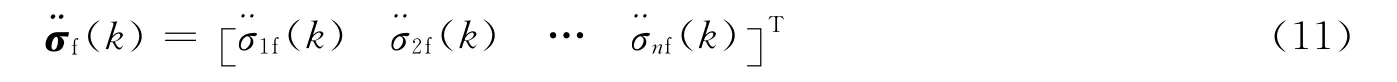
式中 k=0,1,...。考虑到可实现性,需要对前馈的框架角加速度进行一定的限幅。
为简化实现,复合操纵律可依据图1进行。当SGCMG 系统远离奇异状态时,奇异测度较大,则不施加前馈,此时复合操纵律退化为一般动态操纵律;当SGCMG 系统靠近奇异状态时,奇异测度较小,则施加前馈,使系统尽快到达目标框架角,从而回避或逃逸内部奇点。
4 数值仿真验证
为验证操纵律的可行性,在此以某SGCMG 系统为例,进行了仿真研究。SGCMG 系统的运动学方程为[8]
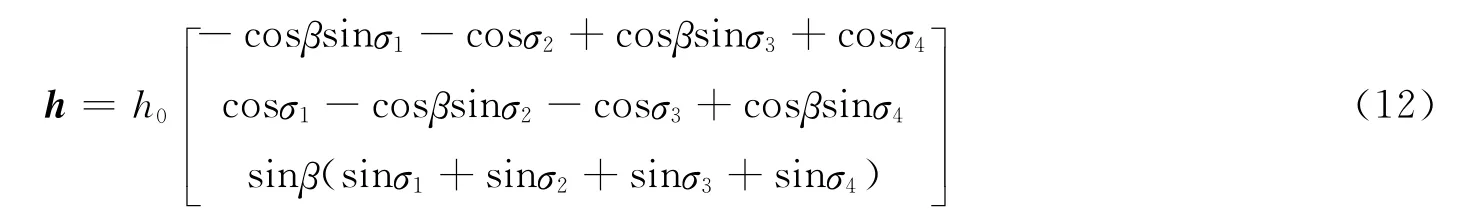
在仿真中,为简便起见,设SGCMG均具有单位角动量(h0=1),β=54.74°,采样周期T=5ms,奇异测度力矩误差采用2-范数表示。选取复合操纵律的参数为:α=1,β=0.01,γ1=73,γ2=0.05,γ3=0.001 75,加入前馈补偿的条件是m <1.2。梯度型伪逆操纵律的形式参见文献[1],零运动系数α取为:当m <0.5时,α=5,当m ≥0.5时,α=0。非对角奇异鲁棒逆操纵律的形式参见文献[2],参数取值为:W1=1,W2=W3=2,W4=3,λ=0.1exp(-0.5|JJT|),ε1=sint,ε2=sin(t +π/2),ε3=sin(t+π)。当期望力矩指令=[1,0,0]T,角动量指令hd(t)=[t,0,0]T时,对复合操纵律(见图1)的奇异回避及奇异逃逸能力进行了测试,并与梯度型伪逆操纵律、非对角奇异鲁棒逆操纵律进行了比较。
(1)奇异回避能力测试
设定初始框架角为[0°,0°,0°,0°]T,在滚动力矩指令下,系统将会遭遇椭圆型奇点[-90°,0°,90°,0°]T,考察梯度型伪逆操纵律、非对角奇异鲁棒逆操纵律、复合操纵律对此奇点的回避能力,仿真结果如图2~图4所示。由图2可以看出,梯度型伪逆操纵律无法回避椭圆奇点[-90°,0°,90°,0°]T,在1.15s左右陷入此奇点,无法逃逸。由于在仿真中没有对框架角速度进行限幅,当SGCMG 系统陷入奇异后,梯度型伪逆操纵律的框架角速度非常高,无法实现。同时,由图3、图4可以看出,非对角奇异鲁棒逆操纵律与复合操纵律都以一定的力矩误差为代价,成功回避了椭圆型奇点[-90°,0°,90°,0°]T。相对而言,复合操纵律力矩精度较高,但非对角奇异鲁棒逆操纵律可以通过参数的适当选择提高精度。
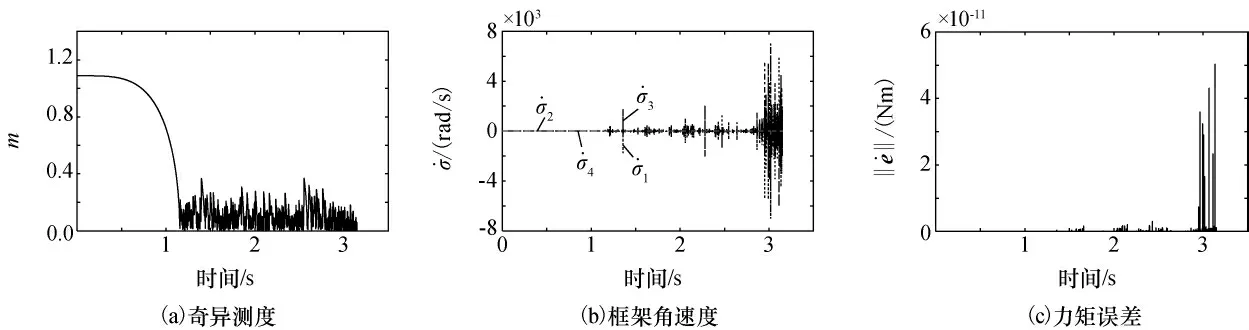
图2 梯度型伪逆操纵律仿真曲线(奇异回避)Fig.2 Simulation curves of the gradient-type pseudo-inverse steering law(singularity avoidance)
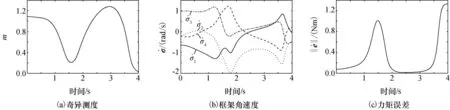
图3 非对角奇异鲁棒逆操纵律仿真曲线(奇异回避)Fig.3 Simulation curves of the off-diagonal singularity robustness inverse steering law(singularity avoidance)
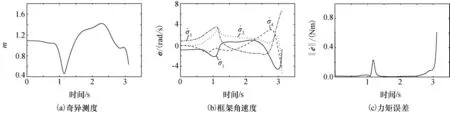
图4 复合操纵律仿真曲线(奇异回避)Fig.4 Simulation curves of the hybrid steering law(singularity avoidance)
(2)奇异逃逸能力测试
为比较梯度型伪逆操纵律、非对角奇异鲁棒逆操纵律、复合操纵律对椭圆型奇点的逃逸能力,在滚动力矩指令下,直接设定初始框架角为椭圆型奇点[90°,0°,-90°,0°]T,仿真结果如图5~图7所示。由图5可以看出,梯度型伪逆操纵律在仿真过程中始终无法逃逸初始椭圆型奇点,且由于没有对框架角速度进行限幅,框架角速度非常高。由图6、图7可以看出,非对角奇异鲁棒逆操纵律与复合操纵律均成功逃离初始的椭圆型奇点,只是以一定的力矩误差为代价。相对而言,复合操纵律脱离奇点的速度较快(小于0.2s),力矩精度较高(优于0.02Nm)。

图5 梯度型伪逆操纵律仿真曲线(奇异逃逸)Fig.5 Simulation curves of the gradient-type pseudo-inverse steering law(singularity escape)
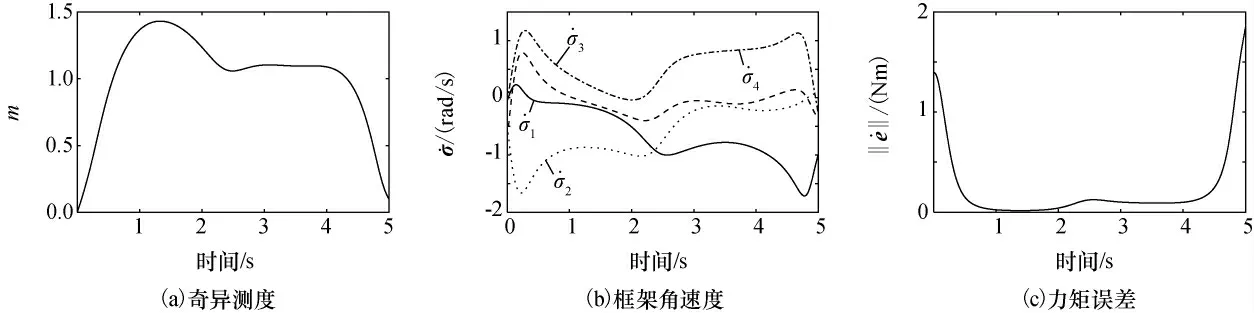
图6 非对角奇异鲁棒逆操纵律仿真曲线(奇异逃逸)Fig.6 Simulation curves of the off-diagonal singularity robustness inverse steering law(singularity escape)

图7 复合操纵律仿真曲线(奇异逃逸)Fig.7 Simulation curves of the hybrid steering law(singularity escape)
综上所述,与梯度型伪逆操纵律相比,复合操纵律通过前馈信号的超前作用,奇异回避及逃逸性能明显占优。与非对角奇异鲁棒逆操纵律相比,复合操纵律奇异回避及逃逸性能接近,但逃离奇点的速度更快,力矩精度更高。
5 结束语
以动态操纵律为基础,设计了一种基于前馈和反馈的复合操纵律。复合操纵律可有效改善SGCMG 系统的奇异回避及逃逸性能,为航天器姿态控制系统提供较高精度的控制力矩。
[1]KUROKAWA H.Survey of theory and steering laws of single-gimbal control moment gyros[J].Journal of Guidance,Control,and Dynamics,2007,30(5):1331-1340.
[2]WIE B.Singularity escape/avoidance steering logic for control moment gyro systems[J].Journal of Guidance,Control,and Dynamics,2005,28(5):948-956.
[3]MENG T,MATUNAGA S.Modified singular-direction avoidance steering for control moment gyros[J].Journal of Guidance,Control,and Dynamics,2011,34(6):1915-1920.
[4]FREDERICK A L,NORMAN G FC.Hybrid steering logic for single-gimbal control moment gyroscopes[J].Journal of Guidance,Control,and Dynamics,2010,33(4):1202-1212.
[5]KRISHNAN S,VADALI S R.An inverse-free technique for attitude control of spacecraft using CMGs[J].Acta Astronautica,1996,39(6):431-438.
[6]PARADISO J A.Global steering of single gimbaled control moment gyroscopes using a directed search [J].Journal of Guidance,Control and Dynamics,1992,15(5):1236-1244.
[7]ZHANG JINJIANG,LI JISHU.Study on steering law of large spacecraft SGCMG system based on fuzzy decision [J].Chinese Journal of Aeronautics,2001,14(2):100-105.
[8]吴忠.单框架控制力矩陀螺动态操纵律设计 [J].宇航学报,2005,26(1):24-28.WU ZHONG.Dynamic steering law design for redundant single gimbal control moment gyroscopes[J].Journal of Astronautics,2005,26(1):24-28.
[9]吴忠,吴宏鑫.SGCMG 系统非奇异路径规划 [J].控制理论与应用,1999,16(1):21-26.WU ZHONG,WU HONGXIN.Nonsingular path planning in single gimbal control moment gyroscope systems[J].Control Theory and Applications,1999,16(1):21-26.
