指数分布具有耐抗性质的参数估计①
尹菊芳, 庄海军, 高 敏
(1.吉林省实验中学,吉林 长春130022;2。公主岭市第三中学,吉林 公主岭136100;3.吉林师范大学,吉林 四平136000)
指数分布是寿命试验和可靠性理论中最常用的分布,相关的统计推断理论也一直是统计学家关心的问题(参见文献[1 ~3]). 以往文献中得到的关于指数分布参数的估计量对于数据的局部不良行为反应比较敏感,也就是说不具有耐抗性. 具有耐抗性的统计量,当部分数据改变,即使这一部分数据与原来的数据差别很大,结果也不会有太大的改变.耐抗方法重视数据的主体部分,而不重视数据当中的离群值. 分位数是耐抗统计量,但样本均值和样本方差却都不是. 众所周知,再好的数据也难免有一小部分数据存在一定的错误或重大偏差,因而如果想要防御这些数据给我们的统计结果带来较大的负面影响,我们必须关注耐抗性. 文献[4]讨论了一类特殊均匀分布具有耐抗性质的参数估计问题.本文进一步讨论指数分布具有耐抗性质的参数估计问题,利用样本的四分位矩这样具有耐抗性质的统计量,对指数分布的参数做出估计. 与此同时,我们也讨论了估计量的优良性.
定义1 设X,X,…X 是来自某总体的简单随机样本,X(1)≤X(2)≤…≤X(n)是相应的次序统计量,定义样本中位数的深度,四分数的深度,其中[x]表示不超过x 的最大整数. 在四分数的深度k 的基础上,进一步定义样本下四分数样本上四分数以及样本四分位矩dF= FU- FL
引理1[5]若n,则数列{an}存在极限,其极限c 为尤拉常数,c = 0.577216….
证明: (1)首先我们求总体的四分位矩:
其次求样本四分位矩(分n = 4m,n = 4m +1,n = 4m +2,n = 4m +3 四种情况讨论:首先讨论n= 4m 情形:中位数深度,四分数深度k,上四分数,下四分 数用样本的四分位矩估计总体的四分位矩得参数θ 的估计同理可得,当n = 4m +1 时,当n = 4m +2 时,当n = 4m+3 时
由文献[6]定理2 可知E(X(k)) =.首先考虑n = 4m 情形. 注意到

令

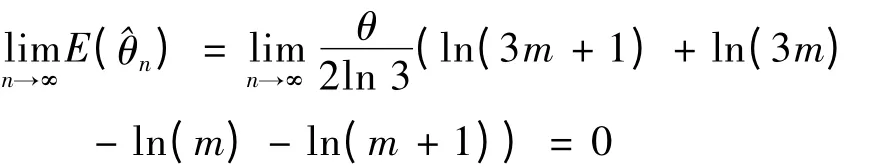
同理,当n = 4m +1,n = 4m +2 以及n = 4m +3 时,= θ 因此是θ 的渐近无偏估计.
[1] 赵海兵,程依明. 指数分布场合下无失效数据的统计分析[J]. 应用概率统计,2004,20(1):59 -65.
[2] 蒋福坤,刘正春. 指数分布参数的区间估计和假设检验[J].嘉兴学院学报,2004,16(3):12 -14.
[3] 蒋福坤,刘正春. 两指数分布总体参数比的区间估计[J]. 浙江教育学院学报,2007,(1):46 -50.
[4] 赵志文,徐江.关于一类特殊均匀分布的具有耐抗性质的参数估计[J].吉林师范大学学报,2004,(4):11 -12.
[5] 刘玉琏,傅沛仁. 数学分析讲义[M]. 北京:高等教育出版社,1995.
[6] 周莉,张维华.利用次序统计量估计指数分布的均值和方差[J]. 锦州师范学院学报,2000,21(3):69 -70.

