Burgers方程的正交基无网格Galerkin解法

陈维维, 赵凤群, 路小平

(西安理工大学 理学院， 陕西 西安 710054)

0 引言

无网格法是近年来兴起的一种数值计算方法，用有限元方法解决问题时出现的困难，有时用无网格法求解则有明显的优势.因此无网格法逐渐成为计算力学一个十分吸引学者研究的课题.它最大的优点就在于部分或彻底的消除了网格对节点的约束，采用节点所在的影响域内的信息构造数值逼近.目前已经提出了十余种无网格法，如：无网格局部Petrov-Galerkin法[1]、再生核粒子法[2]、无网格伽辽金法[3]、光滑粒子流体动力法等[4].特别地，由Belytschko等人提出的无网格伽辽金法(Meshless Galerkin Method)已被成功的应用到工程力学中的许多领域，该方法优点在于采用移动最小二乘法[5](Moving Least Squares，简称MLS构造近似函数)构造的近似函数具有较高的光滑连续性，保证了计算结果不仅具有较高的精度而且还有比较好的稳定性，缺点是在计算形函数和形函数的导数过程中都要计算矩阵的逆，这样又会导致计算效率低，当基函数的项数较大时容易使方程组产生病态.为了克服无网格Galerkin法的上述弊端，本文在无网格伽辽金法中使用正交基函数，使矩阵求逆变得简单，不但避免了产生病态方程组的可能，而且提高了计算效率.对于Burgers方程，在时间域上用θ加权法[6]进行离散，而空间域上采用正交基无网格Galerkin法进行离散，构造了一种新的数值计算方法θ加权-正交基无网格Galerkin法.

1 无网格Galerkin法的基本理论

1.1 移动最小二乘近似

在求解域Ω中，函数u(x)可近似为uh(x)，求解域中插值节点的集合为{x1,x2,…,xN}，则函数u(x)的移动最小二乘近似式uh(x)可以定义为[7,8]

(1)

式中uh(x)为函数u(x)的近似表达式.pi(x)基函数，m是基函数的个数，系数ai(x),i=1,2,…,m是空间坐标x的函数.

为了求得系数a(x)，我们可以采用局部近似的加权最小二乘法拟合求解，即使局部近似误差泛函J取极小值

(2)

式中，w(x-xi)是带有紧支撑性质的光滑连续权函数，即在x的影响域内部，w(x-xi)>0，在其边界和外部，w(x-xi)=0，n是积分点x邻域内的节点数.

由于J取极小值，由极值原理可得

(3)

其中的矩阵A(x)、B(x)分别是：

A(x)=pTw(x)p′B(x)=pTw(x)

当矩阵A为非奇异矩阵时，由(3)可解得

a(x)=A-1(x)B(x)u

(4)

将a(x)代入(1)式中，得到逼近函数uh(x)的表达式是

uh(x)=pT(x)A-1(x)B(x)u=φ(x)u

(5)

其中，φ(x)=pT(x)A-1(x)B(x)，φ(x)是MLS形函数.

1.2 基于正交基函数的移动最小二乘近似

在上述移动最小二乘法中，如果基函数的个数m较大时，方程(3)有可能产生病态，甚至有可能是奇异的，这样就导致该方程很难求出解.为了克服这一问题，可将基函数取为正交函数，这样不仅可以避免所得方程病态或者奇异，而且避免了求矩阵的逆，简化了计算.

对于权函数{wi}和点集{xi}，如果函数p1(x),p2(x),…,pm(x)满足条件

(6)

如任意给出一组基函pk(x) (k=1,2,…,m) 通过下述过程可将基函数pk(x)转化为正交基函数qk(x)

令q1(x)=p1(x)

⋮

(7)

由此(4)式中的矩阵A可化为

(8)

这时将对角化后的矩阵A带入(4)式可求解出系数

(9)

将系数aj(x)代入(5)式可得

uh(x) =qT(x)A-1(x)B(x)ui

(10)

其中Ni(x)是构造好的新的形函数.

为了验证正交基函数的移动最小二乘近似的有效性，取如下的函数进行计算分析：

f(x,y)=(2x+sin(x))3·(ycos(y))4

本文选取高斯函数作为权函数，基函数取pT(x,y)=(1,x,y)，使用20×20个均匀分布节点进行计算，图1和图2分别给出了上述函数关于x和y的偏导的近似结果.

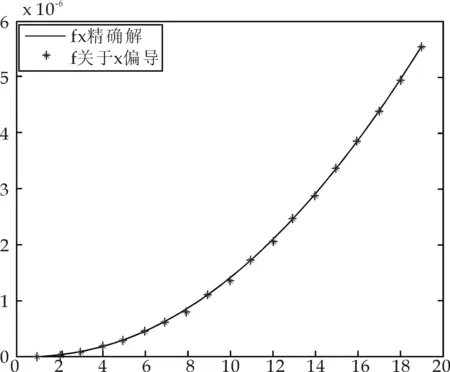
图1 f关于x的偏导数逼近(y=11)

图2 f关于y的偏导数逼近(x=8)

由图1和图2可以看出，采用正交基函数的移动最小二乘近似方法进行函数逼近时，函数偏导数的数值解和精确解逼近效果很好，这就证明了该方法能很好地应用于函数逼近的问题中，同时也表明了该方法的有效性.

2 偏微分方程的无网格Galerkin法离散

考虑如下形式的Burgers方程

(11)

首先，采用θ加权法对方程(11)的时间域进行离散，则有

(12)

将(12)式代入方程(11)则得到关于时间域离散的半离散方程

(13)

其次，采用θ加权-正交基无网格Galerkin法对空间域进行离散，设uh(x)=Nui，并用罚函数处理边界条件，则原方程可化为如下方程组：

(k1-Δtθk2)un+1=[Δt(1-θ)k2+Δtk3-k1]un

(14)

3 数值算例

图3 不同时刻的数值解

图3给出了当t=0.0,0.01,0.1,0.15,0.2,0.25时用本文方法计算出的结果.由图3可以看出，随着时间步长的变化，用θ加权-正交基无网格Galerkin法求解Burgers方程，可以有效的避免数值振荡.

表1给出了粘性系数ε=0.01在不同点处不同时刻的数值解，并与精确解和文献[9]的算法数值解进行了比较，可以看出本文的数值解和精确解很吻合，表明本文的方法是很有效的.

表1 ε=0.01,N=40,Δt=0.000 2时刻所得的数值解及与文献[9]的对比

4 结束语

本文在传统的无网格Galerkin法中引入了正交基函数，形成正交基函数的无网格伽辽金法，对时间域的离散引入了θ加权法，构造出了一种θ加权-正交基函数无网格伽辽金法，并成功的将该方法应用于求解Burgers方程中.由于Burgers方程是典型的抛物型偏微分方程，所以θ加权-正交基函数的无网格Galerkin法也可以作为一种有效的数值方法用于求解其他的抛物型偏微分方程.此外，由于正交基函数的无网格方法简化了数值计算的前处理过程，所以选用正交基函数的无网格Galerkin方法求解一些偏微分方程也具有一定的优势.

[1] S.N.Atluri,T.Zhu.A new meshless local petrov-galerkin(MLPG) approach in computa-tion mechanics[J].Computational Mechanics,1998,22(2):117-127.

[2] W.K.Liu,S.Jun,Y.F.Zhang.Reproducing kernel particale methods[J].Numerical Method in Fluids,1995,20(8):1 081-1 106.

[3] T.Belytschko,Y.Y.Lu,L.Gu.Element-free Galerkin method[J].Numerical Methods in Engineering,1994,37(2):229-256.

[4] M.R.Bate,A.Burkert.Resolution requiements for smoothed particle hydrodynamics calculations with self-gravity[J]. Monthly Notices of the Royal Astronomical Society,1997,228(4):1 060-1 072.

[5] 张 雄，刘 岩.无网格法[M].北京：清华大学出版社，2004.

[6] J.Done,A.Hnerta.Finite Element Methods for Flow Problems[M].England:Wiley,2003.

[7] Belytschko T,Krongauz Y,Organ D.Meshless methods:an over view and recent developments[J].Computer Methods in Applied Mechanics and Engineering,1996,139(1):3-47.

[8] 张 雄，宋康祖，陆万明.无网格法研究进展及其应用[J].计算力学学报，2003，20(6): 730-742.

[9] 刘万海，孙健安.用五次B样条Galerkin有限元方法求Burgers方程的数值解[J].西北师范大学学报，2009，45(2)：35-38.