基于HMM和匹配追踪的多参数语音识别

无锡机电高等职业技术学校自动化工程系 郭 昕

1.引言

语音识别的研究工作始于20世纪50年代，1952年Bell实验室开发的Audry系统是第一个可以识别10个英文数字的语音识别系统。隐马尔可夫模型是20世纪70年代引入语音识别理论的，它的出现使得自然语音识别系统取得了实质性的突破。目前大多数连续语音的非特定人语音识别系统都是基于HMM模型的。[1]

一般来说，语音识别的方法有三种：基于声道模型和语音知识的方法、模板匹配的方法以及利用人工神经网络的方法。语音识别一个根本的问题是合理的选用特征。特征参数提取的目的是对语音信号进行分析处理，去掉与语音识别无关的冗余信息，获得影响语音识别的重要信息，同时对语音信号进行压缩。非特定人语音识别系统一般侧重提取反映语义的特征参数，尽量去除说话人的个人信息；而特定人语音识别系统则希望在提取反映语义的特征参数的同时，尽量也包含说话人的个人信息。

而随着时频技术的研究发展，使人们在进行信号处理时，可以将语音信号分解在一组完备的正交基上。从而，语音信号的能量在分解以后将分散分布在不同的基上。但是，语音信号是一种典型的非平稳信号，其性质随时间快速变化，在两个不同的时间瞬间，在同一个频率邻域内，信号可以有完全不同的能量分布。因此，有必要找到一种精确表示语音信号时频结构，便于特征提取的方法。[2]

立足于此，本文提出，通过平移窗口，用余弦基乘以窗口函数，构造出局部余弦基，分离不同时间区间，很适合于逼近语音信号。本文使用这种具有活动窗口特性的局部余弦基表示语音信号。为了减少计算量，并进一步提高局部余弦基原子时频分布的分辨率，采用匹配追踪(MP)算法分解信号，并结合时频分析技术得到最优局部余弦基原子的魏格纳-维利分布(WVD)[2]，从而得到信号精确的时频结构[3]，进行特征提取。此外，结合语音信号的美尔频率倒谱系数(MFCC)一起作为该信号的特征向量，通过隐马尔科夫(HMM)模型进行识别。实验证明。这种多参数语音识别算法提高了识别的准确度和速度。

2.局部余弦基建模

通过光滑地划分时间序列为任意长度的子区间 [a p,ap+1](如图1)，可使每一个时间段分别由重叠正交基表示，而整个时间序列的基函数又构成时频平面的正交铺叠，因此局部余弦变换对在不同时间段有不同的波形的语音信号有很强的针对性。

图1 重叠窗口划分时间轴Figure1 lapped window divides time axis

图1中g p(t)为重叠窗口函数[3]：

式中β为单调递增的轮廓函数，定义为[3]：

局部余弦函数族构成了实数轴上平方可积函数空间的规范正交基：

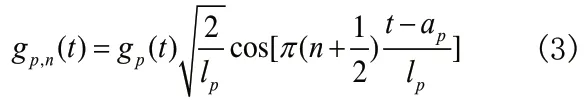
式中lp为窗口支集伸缩参数；ap为第P段时间起点；n(0 ≤n≤lp)表示正交基序列号。

语音信号可表示为：

gγn(t)是余弦基原子，γ=(a p,lp,η)。其中ap是窗口支集边界参数，lp为窗口支集伸缩参数，η是轮廓函数β的尺度参数，这保证了窗口支集只与相邻的具有适当对称性的窗口重合，达到局部余弦基精确覆盖整个时频平面的目的。

3.匹配追踪法选取最佳基

由Mallat和Zhang引入的匹配追踪算法运用贪婪技巧减少了计算的复杂性。它从局部余弦基构成的冗余字典中一个一个挑选向量，每一步都使信号的逼近更为优化。

MP算法将信号分解成一簇时频原子的线性表达，这些原子选自高冗余度的函数字典中，且最好地符合f(t) 内在结构。假设函数集是Hilbert空间中一个完备字典满足，最优的M阶近似为：

设由M个时频函数近似的信号与f(t) 的误差ε最小，ε表达式如下：

其中{γi}i=0...M代表所选函数gγi的索引。

首先按照某个选择函数（与f(t) 的内积最大）逐个挑选出时频函数g0γ，f(t) 分解为：，设初始输入信号f(t)为初始残差信号R0f，Rf表示f(t)在gγ0方向上近似后的冗余部分。

假设已有M

R f表示经过前M-1次迭代后，f(t)中未表达部分：选定为最匹配R Mf的时频函数，R Mf按如下公式分解为：

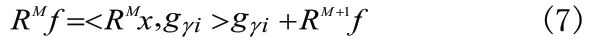
由于每步中R M+1f与gri正交，如果字典是完备的，则迭代收敛于f，满足：

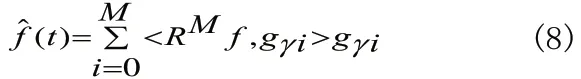
这样，可估算出(4)式中局部余弦基原子的参数bn=＜R Mf,gγi＞。

文献[4]中提出，选出最匹配信号的基，对每一个基求出其WVD分布，信号f(t) 的WVD分布就表示其最优基的WVD的线性组合，这样就消除了交叉项的影响。由此得到f(t) 的WVD分布：

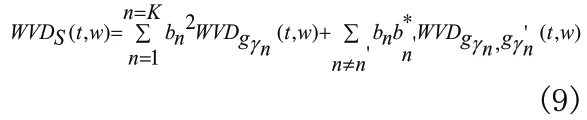
WVDgγn(t,w)是局部余弦基字典中被选中的最优基的WVD分布。将等式左边第二项交叉项组合去除，这样在时频面上就得到了干净的时频表示：

在语音信号稀疏分解过程中，每步分解都要从过完备原子库中选出与待分解语音信号f(t)或语音信号分解残余R Mf最为匹配的原子gγi，原子是由参数γ=(a p,lp,η)公式(4)决定的。因此语音信号稀疏分解所得原子的 参数γ=(a p,lp,η)可作为语 音信 号的 特征。此外，根据公式(10)，使用匹配追踪法选取的最佳基的WVD分布Es，含有该语音信号重要且独特的信息，也可作为该语音信号的特征。

4.基于HMM的语音识别算法

特征提取基于语音帧，即将语音信号分为有重叠的若干帧，对每一帧提取一次语音特片。由于语音特征的短时平稳性，帧长一般选取20ms左右。在分帧时，前一帧和后一帧的一部分是重叠的，用来体现相邻两帧数据之间的相关性，通常帧移为帧长1/2。本文为了方便做MP，采用的帧长为512点(32ms)，帧移为256点(16ms)。特征的选择需要综合考虑存储量的限制和识别性能的要求。通常的语音识别系统使用24维特征矢量，包括12维MFCC和12维一阶差分MFCC。本文提出的多参数语音识别算法，在此基础上增加了原子参数γ=(a p,lp,η)公式(4)和最佳基的WVD分布Es公式(10)，这两维特征，构成26维特征矢量。对MFCC和语音信号能量的WVD分布Es分别使用了倒谱均值减CMS(Cepstrum Mean Subtraction)和能量归一化ENM(Energy Normalization)的处理方法提高特征的稳健性[5]。

在HMM模型中，首先定义了一系列有限的状态S1，…，SN，系统在每一个离散时刻n只能处在这些状态当中的某一个Xn。在时间起点n=0时刻，系统依初始概率矢量π处在某一个状态中，即：

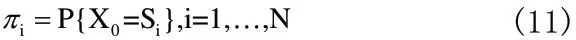
以后的每一个时刻n，系统所处的状态Xn仅与前一时刻系统的状态有关，并且依转移概率矩阵A跳转，即：

系统在任何时刻n所处的状态Xn隐藏在系统内部，并不为外界所见，外界只能得到系统在该状态下提供的一个Rq空间随机观察矢量On。On的分布P称为输出概率矩阵，只取决于On所处状态：

因为该系统的状态不为外界所见，因此称之为“隐含马尔科夫模型”，简称HMM。在识别中使用的随机观察矢量就是从信号中提取的特征矢量。按照随机矢量Qn的概率分布形时，其概率密度函数一般使用混合高斯分布拟合。

其中，M为使用的混合高斯分布的阶数；Cm为各阶高斯分布的加权系数。此时的HMM模型为连续HMM模型(Continuous density HMM)，简称CHMM模型[6]。在本识别系统中，采用孤立词模型，每个词条7个状态，同时包括首尾各一个静音状态；每个状态使用3阶混合高斯分布拟合。

5.仿真实验

5.1 提取最佳基的WVD分布特征矢量

构建局部余弦基字典，使用MP算法选取语音信号“A”的最佳基。如图2所示。得到的E s(t,w)时频图既保留了余弦基原子高时频聚集性的优点，又削弱了WVD作为二次型时频表示所固有的交叉项的影响，得到了干净的时频面。其结果更精确的反映出语音信号在频率、音强方面的特征，具有良好的时频聚集性。

图2 “A“信号的WVD分布Figure2 WVD of“A”

5.2 孤立词识别

在语音识别实验中，采用信号长度为1024的200个实际语音信号样本，其中100个用于训练，100个用于测试。该实验用以识别出语音信号”A”。实验利用WaveCN2.0录音系统进行样本采集，采样率为8kHz。得到语音信号的有效部分后，提取样本信号的MFCC参数作为语音信号的特征参数之一。Mel滤波器的阶数为24，fft变换的长度为256，采样频率为8kHz。MFCC的相关波形见图3。

图3 “A“信号的MFCC波形Figure3 MFCC Waveform of“A”

然后利用MP算法将样本信号分解为300个原子，将所得原子的参数γ=(a p,lp,η)和最佳基的WVD分布Es，作为该语音信号的特征参数之二。见图2。通过HMM进行识别。

在实验中，设语音”A”类值为1，其他的语音类值为-1。HMM模型的状态数为7，高斯混合数为3。由第4节HMM训练的定义可知，重估过程中的输出概率是随着重估次数的递增而增加的，图4列出了“A”模型训练期间重估次数与总和输出概率的log值之间的关系。由图可以看出，“A”模型重估20次算法收敛，并且，输出概率与重估次数成正比趋势。

图4 重估次数与总和输出概率Figure4 Iterations of EM and output like lihood

对语音进行上述HMM训练之后，将其模型参数存贮，获得了识别的HMM模型库。在识别阶段，对100个测试用数据进行语音识别，以检验本文系统的识别效果。如表1所示识别精度为89%，平均识别时间约为1.313秒，实验结果表明，系统识别率和运算速度都比较理想。

表1 识别结果

增加了局部余弦基原子的参数γ=(a p,lp,η)和最佳基的WVD分布Es作为特征参数，较单纯的使用MFCC作为特征参数进行HMM模型训练，识别率有一定提高，见表2。

表2 结果比较

6.结语

本文在传统基于HMM模型的语音识别基础上，通过匹配追踪算法，提取出最佳基的原子参数γ=(a p,lp,η)和WVD分布Es。二者与MFCC一起，作为本文提出的多参数语音识别算法的特征向量。然后选择了大量孤立词样本进行仿真实验，针对非特定人孤立词进行语音识别。结果表明，基于HMM和匹配追踪的多参数语音识别算法，可提高语音识别的速度和准确度，有一定的实用性。但是，由于算法的复杂性增加，运算量相应增大，简化算法运算量仍是需要深入研究的课题。

[1]何方伟，青木由直.DP动态匹配算法实现语音的实时识别[J].数据采集与处理，vol.4，no.1，Mar，1989.

[2]R.R.Coifman，M.V.Wickerhauser.Entropy-based algorithms for best basis selection[J].IEEE Trans.Info.Theory，38(2)：713-718，March 1992.

[3]S Mallat，Z Zhang.Matching Pursuit with Time-Frequency Dictionaries[J].IEEE Trans.Signal Processi ng，1993，41(12)：3397-3415.

[4]R Gribonval.Fast matching pursuit with a multiscale dictionary of Gaussian Chirps[J].IEEE Trans.Signal Processing，2001，49(5)：994-1001.

[5]于建潮，张瑞林.基于MFCC 和LPCC的说话人识别[J].计算机工程与设计，2009，30(5)：1189-1191.

[6]王作英，肖熙.基于段长分布的HMM语音识别模型[J].电子学报，2004，vol.32，no.1：46-49.