光学图像高斯平滑滤波的DSP优化

汤 达，牛照东，王丁禾，陈曾平，李晓鹏

(1.国防科学技术大学ATR重点实验室，湖南 长沙410073;2.中国人民解放军77108部队，四川 成都611233)

1 引言

光学传感器在传输、接收和处理图像数据的过程中，往往会存在一定程度的噪声干扰，恶化了图像的质量。高斯平滑滤波具有优良的噪声平滑性能和边缘保留能力，适合平滑图像、去除噪声，但运算量较大，限制了其在实时图像处理系统中的应用。因此，有必要对高斯平滑滤波算法进行优化，使其满足图像处理系统的实时性需求。

目前，已有专家学者针对算法的硬件优化进行研究，并取得了一定的成果。文献［1］、［2］介绍了DSP代码开发流程以及代码优化的思路与方法，但并未结合实例进行具体说明;陈松［3］等人对三种图像预处理算法进行了优化，但同样缺乏对优化方法的详细陈述;雷涛［4－5］等人提出了一种空域低通滤波优化方法，但该方法对滤波掩膜的系数取值有严格的限制，具有较大的局限性;黄德天［6］等针对中值滤波进行了不同程度的优化，取得了较好的效果，但其优化方法仍有较大的改进空间。

本文基于 TMS320C6x 系列［7－8］定点处理器，利用高斯滤波掩膜的可分解性，提出了一种单次遍历实现两次卷积的高斯平滑滤波DSP优化方法。实验结果表明，该方法能够显著提升滤波效率，达到了算法优化的目的。

2 基本的空域滤波优化方法

空域滤波在图像空间中的实现是通过在待处理图像中逐点移动掩膜进行卷积来完成的。常用的掩膜尺寸为3×3或5×5，掩膜系数随功能变化而变化。图1给出了两种尺度的高斯平滑掩膜，用于平滑图像、减小噪声。本文就以图1(a)所示5×5高斯平滑掩膜为例，说明对空域滤波的优化，对其他尺度滤波掩膜，同样可借鉴本文优化思想。

图1 两种高斯平滑掩膜Fig.1 Two Gaussian smoothing masks

图2描述了传统的空域滤波过程，A0等点代表待滤波图像数据，虚线方框表示滤波掩膜遍历至C2点时，滤波掩膜覆盖到的图像区域。将该区域内每个点的像素值与掩膜对应位置滤波系数相乘，累加后除以滤波系数总和，即可得到滤波结果R11。如此，对单个像素点滤波，需要25次乘法运算、24次加法运算和1次除法运算。

分析传统空域滤波耗时原因，不难发现，其中存在大量的数据重复访问。如对C2、C3两点的滤波均用到了C1至C4点所在列图像数据。如果两次滤波过程均读取掩膜覆盖区域内全部图像数据，将造成C1至C4点所在列图像数据重复读取。C6x编译器访问存储器是很费时的，为了提高数据处理率，应使一条Load/Store指令能够访问多个数据［9］。针对上述问题，利用内联函数［10］_memd8()，一次读取图2中第一行A0到A7的全部8个原始图像数据。如此，只需五条数据读取指令，就可以读取图2所示全部图像数据，同时对多个点进行滤波。

作为一种快速求点积和指令，_dotpsu4()函数将32位输入src1与src2的每8位对应相乘后的累加值作为结果输出，可实现同一行中4个相邻图像数据与滤波系数的相乘后累加工作。鉴于此，对图2所示图像区域内C2至C5点，调用_dotpsu4()函数分别计算相应覆盖区域与滤波掩膜的卷积和，除以滤波系数总和，即可得到滤波结果R11、R12、R13和R14。

图2 5×5空域滤波示意Fig.2 5 ×5 Gaussian smoothing

利用上述方法，每次读取40个图像数据，可计算同行相邻4个像素点对应的滤波结果。其中，对单个像素点的滤波需要调用10次_dotpsu4()函数。横向遍历原始图像，对一个宽、高各为M和N原始图像，遍历MN/4次，即可得到空域滤波后结果图像。

3 高斯平滑滤波优化

3.1 高斯平滑掩膜的可分解性

在空域滤波的实际应用中，为了减少运算量，通常会在满足滤波性能的前提下，有针对性地设计滤波掩膜。常用的方法是利用两个一维滤波掩膜的逐次卷积来代替二维滤波掩膜，而高斯平滑滤波就是其典型代表。

二维高斯滤波掩膜(i，j)处滤波系数取值如下:

式中，(i0，j0)为掩膜中心位置坐标;σ为高斯分布参数，决定高斯函数的平滑程度;c为归一化系数。令一维高斯掩膜滤波系数取值如下:

由式(1)、式(2)，以及高斯掩膜的中心对称性，有:

式中，W为掩膜宽度。由式(3)，进一步得到二维高斯掩膜g(σ;i，j)与两个相互垂直的一维高斯掩膜g(σ;i)、g(σ;j)之间满足:

结合式(4)，将 g(σ;i，j)与待滤波图像 f(i，j)卷积，可得:

式(5)说明了高斯平滑掩膜的可分解性［11－12］，二维高斯平滑掩膜与图像卷积等效于将图像与一维高斯平滑掩膜卷积，然后再将卷积结果与方向垂直的一维高斯平滑掩膜进行卷积。这样，对单个像素点滤波，只需要10次乘法运算、8次加法运算和2次除法运算，大大减少了计算量。

3.2 高斯平滑滤波优化

高斯平滑掩膜的可分解性为高斯平滑滤波的进一步优化提供了理论基础。鉴于此，将5×5滤波掩膜分解为5×1横向掩膜N与1×5纵向掩膜M的相乘，高斯平滑滤波等效于原始图像先与M卷积(以下称横向卷积)后再与N卷积(以下称纵向卷积)。接下来，本文从以下几个方面考虑，对逐次卷积过程进行优化。

3.2.1 基本运算单元

为了最大限度减少算法耗时，应避免对滤波中产生的中间结果进行存取操作，这就要求上述逐次卷积过程应在一次遍历中完成。在明确这一需求后，需进一步确定每次遍历读取多大的图像区域作为基本运算单元进行逐次卷积，能使优化效果达到最优。

为了借助_mem4()函数实现对滤波结果的快速存储，应使每次遍历算得的滤波结果在行方向上相邻且为4的整数倍。为了借助_dotpsu4()函数实现图像数据与掩膜系数的相乘累加，每次读取同一行中相邻8个图像数据参与横向卷积，同理，每次使同一列中相邻8个横向卷积结果参与到纵向卷积。基于以上两点考虑，选择8×8区域作为卷积的基本运算单元，经横向卷积，得到卷积结果大小为8×4，再经纵向卷积得到滤波结果为4×4大小区域。

3.2.2 重组卷积结果

重组卷积结果的目的就是整合横向卷积结果，以便利用内联函数快速完成纵向卷积。下面借助图3(a)与图3(b)，结合重组横向卷积结果，说明逐次卷积过程。

数据打包读取原始图像数据A0至A7及其正下方7行图像数据，横向卷积得到 F1，G1，H1，I1，…，Fi，Gi，Hi，Ii(i=1，…，8)。利用内联函数_packl4()与_pack2()对F1等进行重组，如对F1至F8，利用式(6)、式(7)，将其组合为2个32位整数data_h与data_l。将data_h、data_l以及滤波系数组合coeff_h、coeff_l一同作为_dotpsu4()函数的输入，利用式(8)计算纵向卷积结果。式中，利用逻辑位移代替除法运算，X为逻辑右移位数。

通过横向卷积结果在两次卷积中的合理过渡，不仅使逐次卷积能够在对图像的单次遍历中完成，且由于逐次卷积过程中大量使用内联函数，使得算法执行效率得到了大幅提升。

3.2.3 复用卷积结果

分别读取原始图像中以像素点(m，n)和(m+4，n)为左上角端点的2组8×8图像数据，各自与M卷积，得到 Fi、Gi、Hi、Ii。两次横向卷积结果前者 i取值从m至m+7，后者i取值从m+4至m+11。可见，后者前一半的卷积结果已由前者算得，无须重复计算，只需再计算后一半卷积结果即可。

图3 优化后滤波计算与流程图Fig.3 Calculation and flow chart of filtering algorithm after optimization

鉴于此，纵向遍历时，除了在图像顶端的初始遍历读取大小8×8图像区域，算得8×4横向卷积结果外，其余遍历时复用前一次遍历产生的4×4横向卷积结果，另外读取4×8基本运算单元，算得可复用于下次遍历的4×4横向卷积结果即可。在获得同等数量滤波结果情况下，复用过程结果，数据读取量与卷积运算量均减半，且滤波过程无多余的数据存取，既节省了时间，又节约了空间。

3.2.4 滤波流程

综上所述，优化后高斯平滑滤波算法步骤如下，m、n初始值均为0。

Step1:数据打包读取图像数据O'=O0n8×8，其中Omn8×8代表以原始图像中(m，n)点为矩阵左上角的8×8图像数据，读取图像数据后将m赋值为8;

Step2:O'的每一行与 M 卷积，得到 F1，G1，H1，I1，…，Fi，Gi，Hi，Ii(i=1，…，8)，记为 T;

Step3:T 的每一列与 N 卷积，得到 Rmn，Rm+1，n，Rm+2，n， Rm+3，n， …， Rm，n+3， Rm+1，n+3， Rm+2，n+3，Rm+3，n+3，除以系数累加和作为滤波结果输出;

Step4:利用式(9)－(12)，复用卷积结果，更新Fi、Gi、Hi、Ii(i=1，…，4);

Step5:数据打包读取原始图像数据 O'=Omn4×8，其中 Omn4×8代表以原始图像中(m，n)点为矩阵左上角的4×8图像数据;

Step6:O'的每一行与 M 卷积，得到 F5，G5，H5，I5，…，Fi，Gi，Hi，Ii(i=5，…，8);

Step7:如果m小于原始图像高度M，m=m+4，重复Step3至Step6，否则跳转至Step8;

Step8:如果n小于原始图像宽度N，n=n+4，跳转至Step1，否则结束滤波。

4 实验结果与分析

为了测试优化性能，利用图1(a)所示5×5高斯平滑滤波掩膜对不同尺寸的原始图像进行滤波，得到优化前后滤波耗时如表1所示。实验仿真环境为 DSP集成开发环境 CCS v3.2，处理器为TMS320C6455/1GHz，处理时间为CCS软件内部剖析时钟显示的程序耗时。

表1 优化前后滤波耗时对比Tab.1 Time cost before and after optimization

由表1，在－o3模式下编译未经优化的高斯平滑滤波代码，对不同尺寸图像的滤波均耗时较长。利用文献［3］所述传统的空域滤波方法进行优化，滤波效率平均提升约16倍。借助高斯平滑掩膜的可分解性，对原始图像进行逐次卷积，该过程首先遍历原始图像进行横向卷积，再遍历横向卷积结果进行纵向卷积。逐次卷积耗时如表1第四列所示，对小尺寸图像的逐次卷积耗时相比传统空域滤波有小幅减小，对大尺寸图像的逐次卷积耗时反而超过了传统空域滤波耗时，这主要是因为两次遍历中横向卷积结果的存取消耗了大量的时间，且图像尺寸越大，存取操作耗时也就越多。利用本文方法，重组并复用横向卷积结果，使逐次卷积能够在对图像的单次遍历中完成，滤波效率较传统优化方法和逐次卷积方法有了进一步的提升。实验结果表明，对不同尺寸的图像，滤波效率提升32倍以上，且图像尺寸越大，滤波效率的提升就显著。

对一幅320×240×8bit图像，利用不同尺度的高斯平滑掩膜进行滤波，得到滤波耗时如表2所示。随着掩膜尺度的增大，掩膜分解前后算法运算量差异就越大。因此，越是大尺度的滤波掩膜，利用本文方法滤波，优化效果也就越显著。

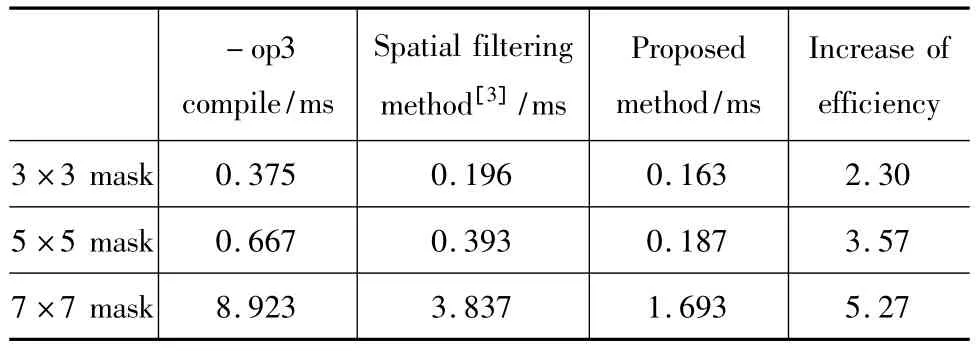
表2 不同尺度掩膜优化性能对比Tab.2 Results of optimization experiments with different scale masks

5 结论

本文以TMS320C6x系列DSP为应用平台，基于高斯平滑掩膜的可分解性，提出了一种单次遍历实现两次卷积的高斯平滑滤波DSP优化方法，首先，依次打包读取4×8图像区域作为基本运算单元，有效降低对数据的重复访问;其次，在基本运算单元内，利用内联函数并行计算横向模板的一次卷积;然后，重组并复用横向模板卷积单元直接进行纵向模板的二次卷积。最后，以基本运算单元为单位遍历处理图像，计算平滑滤波结果。实验表明，本文方法能够显著提升高斯平滑滤波效率，具有较大的工程应用价值。

［1］ Diao Yiping，Zhao Xiaoqun.C code optimization for TI C6000 DSPs［J］.Microcomputer Applications，2007，28(5):544 －548.(in Chinese)刁一平，赵晓群.基于TI C6000DSP的C/C++语言代码效率优化［J］.微计算机应用，2007，28(5):544－548.

［2］ YangGuangyu，Gao Xiaorong，Wang Li，et al.Technology of C/C++Program Optimization Based on TI C6000 DSP［J］.Modern Electronics Technique，2009，33(8):544 －548.(in Chinese)杨光宇，高晓蓉，王黎，等.基于TI C6000系列DSP的C/C++程序优化技术［J］.现代电子技术，2009，33(8):544－548.

［3］ Chen Song，Zheng Hong，Wu Xinghua，et al.Optimization method of digital image preprocessing algorithm based on DSP［J］.Electronic Instrumentation Customer，2010，17(3):58 －60.(in Chinese)陈松，郑红，吴兴华，等.基于DSP的数字图像预处理算法优化方法［J］.仪器仪表用户，2010，17(3):58－60.

［4］ Lei Tao，Cao Xiaowei，Wu Qinzhang.The optimization of the space low－pass filtering module in the real－time image processing based on DSP［J］.Opto － Electronic Engineering，2012，39(5):116 －120.(in Chinese)雷涛，曹晓伟，吴钦章.实时DSP图像处理空间低通滤波模块优化［J］.光电工程，2012，39(5):116 －120.

［5］ Lei Tao，Zhou Jin，Wu Qinzhang.Research on optimization method of DSP real－time image processing software［J］.Computer Engineering，2012，38(14):177 － 180.(in Chinese)雷涛，周进，吴钦章.DSP实时图像处理软件优化方法研究［J］.计算机工程，2012，38(14):177 －180.

［6］ Huang Detian，Chen Jianhua.Code optimization of DSP image processing［J］.Chinese Journal of Optics and Applied Optics，2009，2(5):452 －459.(in Chinese)黄德天，陈建华.DSP图像处理的程序优化［J］.中国光学与应用光学，2009，2(5):452 －459.

［7］ Texas Instruments.TMS320C6455 Technical Reference［EB/OL］.2005.(SPRU965)

［8］ Li Kun，Dong Wenjuan，Wang Weihua，et al.Implementation of a hardware platform for infrared image information processing and optimization of software based on double DSPs［J］.Infrared Technology，2008，30(9):533 － 536.(in Chinese)李坤，董文娟，王卫华，等.基于双DSP的红外图像信息处理硬件平台的实现及软件优化［J］.红外技术，2008，30(9):533 －536.

［9］ Li Fanghui，Wang Fei，He Peikun.The principle and application of TMS320C6000 DSPs［M］.2nd ed.Beijing:Publishing House of Electronics Industry，2003.(in Chinese)李方慧，王飞，何佩琨.TMS320C6000系列DSPs原理与应用［M］.2版.北京:电子工业出版社，2003.

［10］ Texas Instruments.TMS320C64x/C64x+DSP CPU and Instruction SetReference Guide ［EB/OL］.2008.(SPRU732)

［11］ Byung Soo Moon.A gaussian smoothing algorithm to generate trend curves［J］.Korean Journal of Computational and Applied Mathematics，2001，8(3):507 －518.

［12］ Frank Y Shih，Yi－ Ta Wu.Decomposition of arbitrary gray － scale morphological structuring elements［J］.Pattern Recognition，2005，38(12):2323 －2332.