模型故障诊断法在飞机液压能源系统中的应用

刘 东，安云哲，崔建国，谭 峰

(1.沈阳飞机设计研究所综合后勤保障部，沈阳110035;2.沈阳航空航天大学自动化学院，沈阳110136)

故障诊断方法是保证系统能够安全可靠地完成预定目标的重要手段。随着系统的复杂程度不断提高，其可能出现的故障随之增加，用于维护系统的成本也随之升高。为了提高系统的安全性和可靠性的同时减少系统的全寿命周期费用，对故障诊断方法提出了更高的要求:①减少系统的维修和保障时间，进而减少相关的成本;②减小误诊率;③减少关键系统(组件)不工作时间。

传统的基于经验的故障诊断方法主要包括基于规则和基于案例的诊断方法［1，2］。基于规则的诊断方法在早期的故障诊断系统中运用较为广泛，但随着诊断对象的日益复杂，该方法表现出许多缺点:①不能很好地表示复杂、大型的系统知识;②可移植性差，某项规则只适用于该系统，而对于另一系统则需要重新制定规则;③依赖于已有的经验，对未出现过的故障，诊断效果较差。同样基于案例的诊断方法也有类似的缺点。

而对于这些缺点，基于模型的故障诊断方法［3］就可以很好地避免。基于模型的故障诊断方法又称为基于深知识的方法，它利用系统的结构、行为和功能等方面的知识对系统进行诊断推理，需要建立系统的结构、行为或功能模型。Davis R［4］发表的“基于结构与行为的诊断推理”及Reiter［5］的“基于第一定律的诊断理论”奠定了基于模型的故障诊断方法的理论体系。Johan和Williams［6］运用 ATMS(基于假设的真理保障系统)对多故障问题进行了研究。其后，Williams对系统的行为模型建立方法及基于模型的推理算法进行了深入的研究，取得了极大的成果［7－8］。基于模型的故障诊断方法首先需要建立系统(例如液压系统，燃油系统等)基础组件库，然后按照系统的工作结构把所需的组件模型连接起来，再加一些适当的逻辑约束，就形成整个系统的工作模型。对于在此基础上设计的一个新的系统，只需要对新的组件建模即可，可见，基于模型的故障诊断方法的移植性较好。另外，组件库建模型时都考虑了其有可能发生的故障模式，所以经过诊断引擎推理后可以较准确地对故障进行定位，并且确定故障组件的状态。

经过近二十年的发展，基于模型的故障诊断方法已经逐渐从理论研究过渡到工程应用领域，并且得到了广泛的应用。最具代表性的是NASA的 DS-1 中采用的 livingstone［9，10］系统，它是一个基于模型的故障诊断系统，与自主规划器和执行器相结合，可实现系统的在线自主诊断和重配置。

基于组件化建模方式，利用面向对象的建模语言Rodelica建立了飞机液压能源系统各组件的行为模型，并结合模拟的现场数据，经诊断推理引擎，实现了对飞机液压能源系统的故障诊断。

1 基于模型的故障诊断方法

基于模型的故障诊断方法需要建立两类规则:建模规则和诊断推理规则［11］。建模规则描述系统(组件)的功能和行为，以及各个组件之间的相互关系;推理规则(诊断推理引擎)负责把观测值同系统模型的预测值进行比较，若无差异则系统正常，否则利用这些差异来搜索那些可使预测模型与观测值相一致的各种可能行为的状态假设，这些状态假设就是基于模型诊断中的诊断解。基于模型的故障诊断方法的基本思想如图1所示。

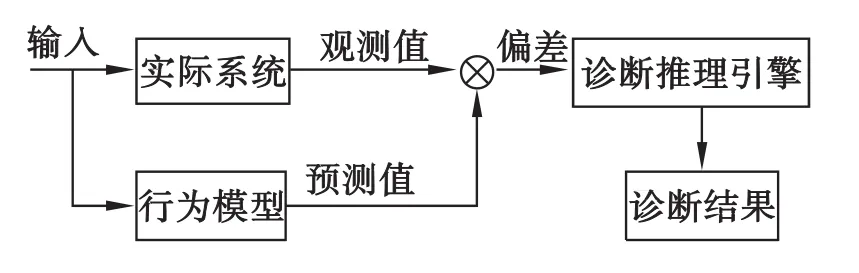
图1 基于模型的故障诊断方法原理图

由图1可知，基于模型的故障诊断方法的第一步是建立实际系统的行为模型，行为模型的建立方法主要分为定量模型和定性模型两种。该诊断系统采用定性模型对所研究的系统进行建模分析，之所以采用定性模型，是因为定性模型是由一组表示系统物理参数的定性变量和一组各参数之间相互关系的定性方程组成，诊断中通过对系统和过程的定性描述和推理，能够有效揭示系统行为之间的内在联系。除此之外，定性模型要求的信息没有定量模型那么多和精确，且诊断周期短，可实现在线自主诊断，并具有较好的抗扰动性。

基于模型的故障诊断系统的主要思想可以通过如图2所示的加法-乘法逻辑电路［12］来加以说明。

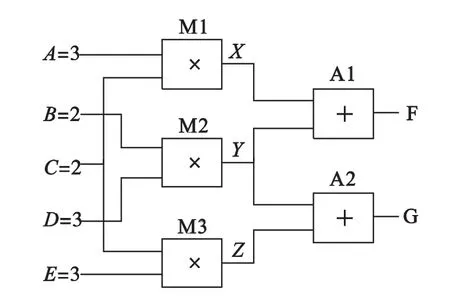
图2 加法-乘法逻辑电路

该系统的输入是 A、B、C、D、E，输出是 F、G。X、Y、Z是系统中可检测或观测到的量。系统包括三个乘法器(M1、M2、M3)和两个加法器(A1、A2)。建立系统模型后仿真得系统在正常情况下，中间量:X=6，Y=6，Z=6;输出:F=12，G=12。

假设某次观测到实际系统的结果为F=10，G=12，可知实际系统的观测值和系统模型的预测值产生了冲突，说明实际系统出现了故障，导致F=10。然后诊断推理引擎就需要针对这个冲突给出一个合理的解释，即找到故障组件以及故障原因。

一个可能的原因是加法器A1出现了故障，导致F=10;也有可能是乘法器M1出现了故障使得中间变量X=4，进而导致F=10;以上只是讨论了系统中单一故障原因，但也有可能是系统中多个组件发现了故障，从而导致输出结果F=10。如若乘法器M2出现了故障使得Y=4，也会导致F=10，但若M3和A2正常的话，G的值应该也为10，而实际G的值是正常值，所以此时M3或A2应该也有故障，才会导致实际系统观测到的现象。通过上述分析就可得到所有可能导致上述冲突的诊断解为{M1}，{A1}，{M2，M3}，{M2，A2}。

接下来就可以通过检测中间变量X、Y、Z的值，来区分是哪个组件的故障导致的冲突，从而定位故障组件。例如经测量得X=4，Y=6，Z=6，由此就可确定是乘法器M1的故障导致F=10。

2 故障诊断系统总体框架设计

针对上文所述的基于模型的故障诊断方法的原理，提出如图3所示的基于模型的故障诊断系统的总体结构框架。

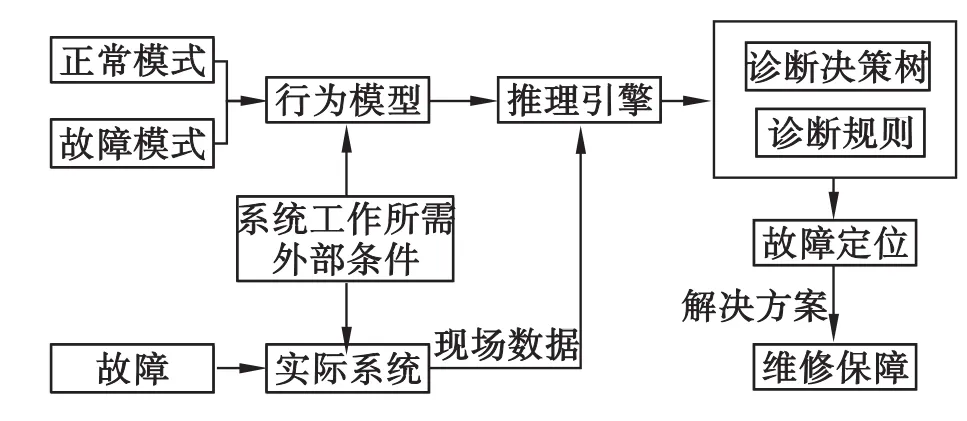
图3 基于模型的故障诊断系统总体框架

2.1 系统架构描述

1)行为模型

在传统的可靠性分析中，故障模式被用来描述组件在其自身发生故障的情况下的行为，同样，正常模式描述了组件在无故障发生时的行为。为了将上述两种模式结合起来，就产生了行为模型这个概念，其具体定义可表示为①定义相关行为模式(正常模式和故障模式)的变量和约束这些变量的数学方程;②描述由于器件内部故障或外部条件触发的不同行为模式之间切换的模型。

将组件的正常模式和故障模式统称为组件的行为模式。假设某一个组件a共有k个不同的行为模式，那么第j(j={0，1，…，k})个行为模式可以定义如下:

其中:xa是组件a中的已知参数向量，ya是组件a中的未知参数向量是组件a的第j个行为模式下的参数之间的函数关系向量。

由上式可知，在组件的行为模型中，组件的各种行为模式之间是相互独立的，在仿真时就可以通过设置j的值，从而可以快速方便地设置组件的行为模式，从而改变组件的行为。

基于上述对组件行为模型的描述，可得如图4所示的组件行为模型建立的基本流程。

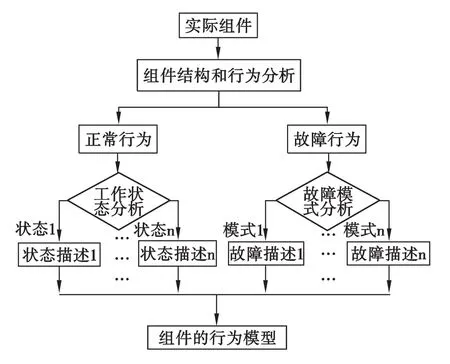
图4 组件行为模型建立流程图

采用建模语言Rodelica建立组件的行为模型。Rodelica最先由瑞典科学家Lunde［13］在故障诊断系统中使用，它继承了基于方程的建模语言Modelica的特点，是一种面向对象的多领域建模工具，支持类、继承等分层结构，采用数学方程描述系统的行为模式。利用Rodelica可以很方便地同时描述组件正常模式下的行为，以及组件在不同的故障模式下的行为。

2)数据采集模块

诊断系统既包括软件部分又包括硬件部分，软件部分是指系统建模、仿真以及诊断程序;硬件部分则是实际的硬件系统。根据诊断系统的需求，需设计数据采集模块，以便实时采集实际系统的数据实现在线的自主式诊断。数据采集模块的方框图如图5所示，由传感器采集现场数据经A/D转换电路转换成数字信号，最后经ModBus总线传至诊断程序中。

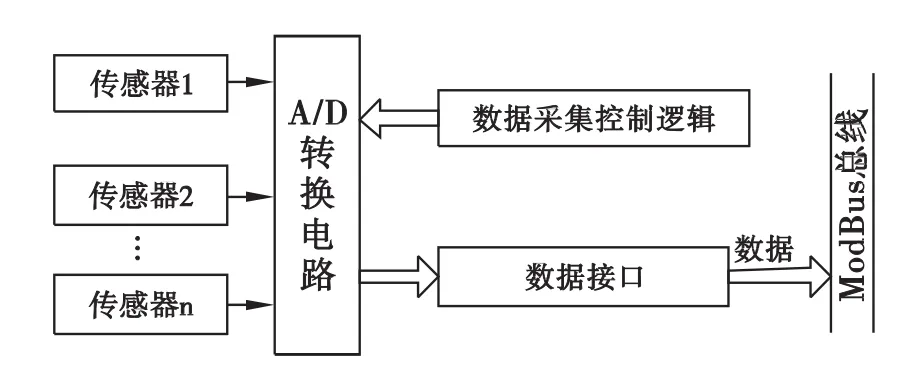
图5 数据采集模块

2.2 故障诊断工作流程

基于以上分析，可按照图6所示流程对实际系统展开故障诊断工作。

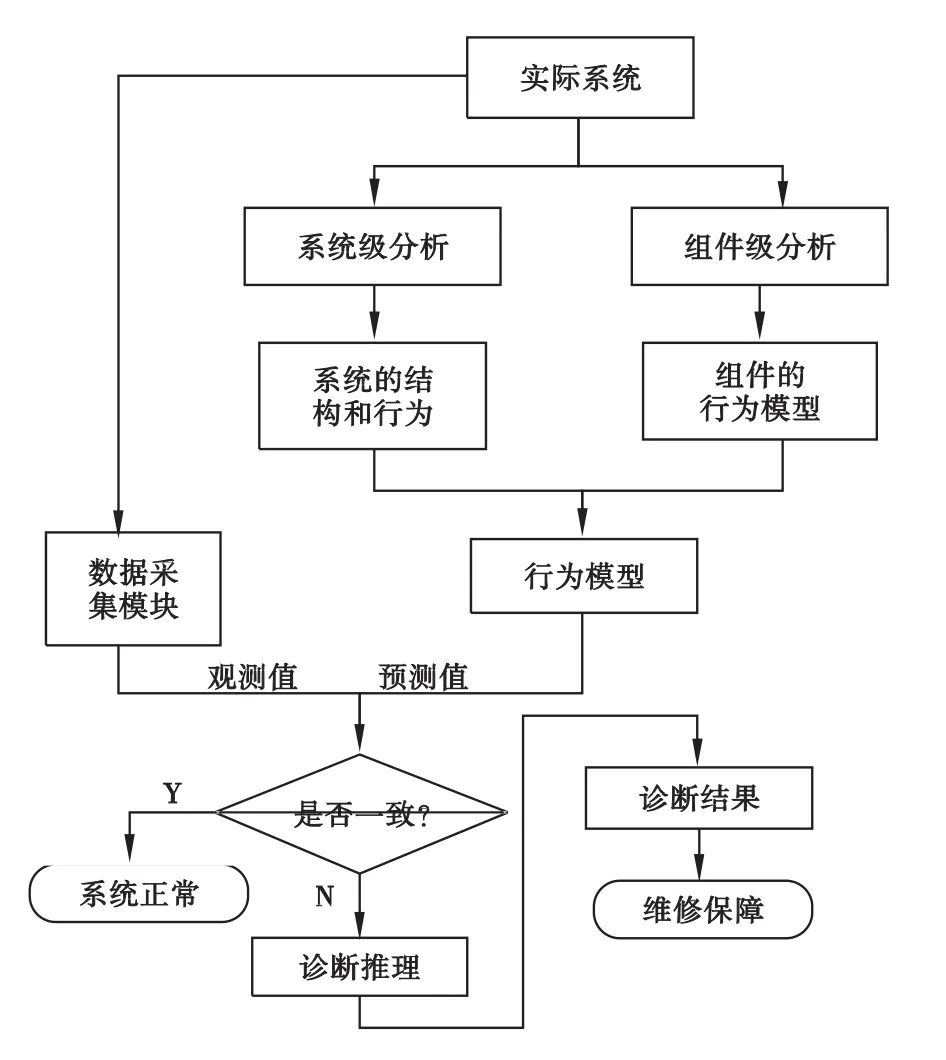
图6 故障诊断工作流程

对系统进行故障诊断，首先需要建立该系统的行为模型，可以通过两方面进行分析:系统级分析和组件级分析。系统级分析的任务主要是分析系统各部分的拓扑结构以及系统的行为和功能;组件级分析则是分析各组件内部自身的功能和行为，既需要描述组件的正常行为，也需要描述组件在不同故障状态下的行为。然后通过数据采集模块采集实际系统的观测值(系统可观测的或可测量的值)，并与系统模型所得的预测值进行比较。若一致，则系统正常，否则所得的预测值与观测值将作为推理引擎的输入，进行故障推理，得出诊断决策树和诊断规则等诊断结果，为定位故障组件和对故障点进行维修等工作提供依据。

3 飞机液压能源系统故障诊断

基于上文所描述的故障诊断系统总体框架，本节将阐述基于模型的故障诊断方法在飞机液压能源系统中的应用。该液压能源系统的原理图如图7所示。其工作原理为恒压液压泵由电动机控制，输出恒压液压油，经滤油器过滤后给负载供油，恒压液压泵的输出流量是由负载控制的。

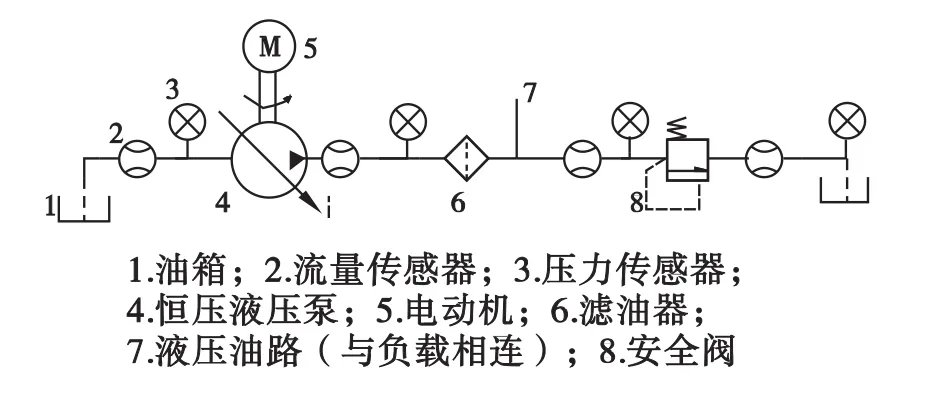
图7 液压能源系统原理图

为了便于模型的建立和故障诊断，该液压能源系统主要由油箱(tank)、恒压液压泵(pump)、滤油器(filter)、安全阀(sv)、节流阀(throttle，充当系统负载)、压力传感器(mP)、流量传感器(mV)等组成。

3.1 行为模型建模

本节以恒压液压泵为例对组件的行为模型的建模过程加以说明。该泵有两个输入，分别是与油箱连接的液压油接口以及电机的控制信号;一个输出是恒压的液压油接口。

该泵有一个正常状态，即输出恒压液压油;有两个故障状态，即泵堵塞所造成的无流量输出;泵内部的泄漏导致输出流量比输入流量少。确定后就可利用面向对象的建模语言Rodelica描述该组件的各种行为模式进行。该泵有以下两个主要方程:

1)功率平衡

其中:pIn是泵的输入功率，pOut是泵的输出功率，pLeak是泵的泄漏功率，pE是控制电机的功率。

2)流量平衡

其中:vIn是泵的输入流量，vOut是泵的输出流量，vLeak是泵的泄漏流量。

本文采用 Rodilica语言建立模型，以下是Rodilica语言对恒压液压泵的部分描述，表示当液压泵堵塞时，入口P1的液压流量为零。

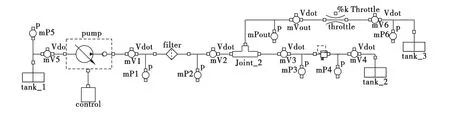
图8 飞机液压能源系统的行为模型

完成组件级建模后，按照系统原理图7，最终建立的液压能源系统的行为模型如图8所示。

3.2 模型校验

采用诊断工具RODON对所建模型进行具体分析校验。首先在仿真系统组件均正常的情况，设置系统相应的初始值，仿真后得到各传感器的值如表1所示。

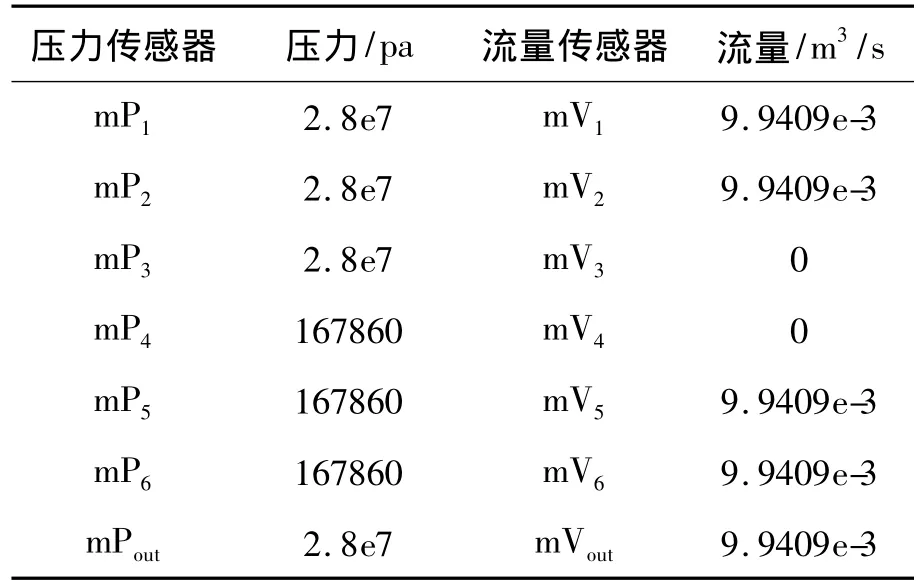
表1 飞机液压能源系统正常时各传感器的值

本系统选用输出压力为28MPa的恒压泵，在不考虑压降的情况下，测量恒压液压泵输出压力的压力传感器mP1及测量转接头joint_2三个接口处压力值的压力传感器mP2、mP3、mPout正常情况下输出相等，压力值为泵的固有参数28MPa。压力传感器mP4、mP5、mP6与油箱连接，所测值为油箱的压力，本系统设定的油箱压力为167860Pa。

恒压液压泵的输出流量是由负载(节流阀)决定的，节流阀是根据两端的压差控制通过的流量。本系统对安全阀设定的安全压力为32MPa，正常情况下安全阀是关闭的，两端流量为零。所以正常情况下，油箱1、恒压液压泵、滤油器、转接头、节流阀以及油箱3形成一条液压通路，各部分的流量相等。由表1可知，本系统所建模型符合实际情况。

接下来就可仿真系统在组件出现故障情况下的行为，RODON可仿真系统单一故障状态或多故障状态下的行为，在此采用单一组件故障情况进行分析校验，以恒压液压泵的无流量输出故障为例进行仿真，得出各传感器的值如表2所示。

由表2可知，当恒压定量泵无流量输出时，各压力传感器所测的压力值均为所设定的系统油箱压力167860Pa，各流量传感器所测的流量值均为零，证明系统行为模型输出正确。

表2 恒压液压泵无流量输出故障时各传感器的值

3.3 故障诊断分析

基于模型的故障诊断方法的原理是在相同的输入情况下，将实际系统的观测值与系统模型的预测值进行比较，若二者有冲突就将二者的偏差输入诊断推理引擎中，从而得到诊断结果。本节以系统出现无流量输出(Vdot_out=0，Vdot_out代表流量传感器mVout的测试值)为例来加以说明。因为实际系统的Vdot_out值和系统模型的Vdot_out值有所偏差，诊断推理引擎就会经历所有可能故障，将可能导致Vdot_out=0的故障定为候选故障，然后再通过观测与候选故障有关的传感器，以确定该故障是否真正发生。通过诊断推理后得出的Vdot_out=0的故障诊断决策树如图9所示。

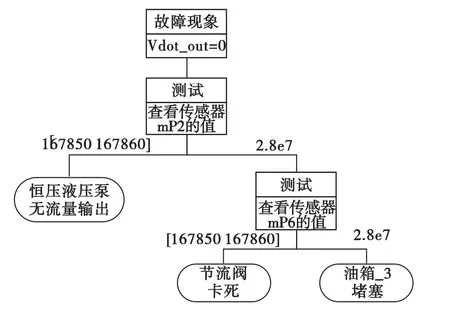
图9 Vdot_out=0产生的诊断决策树

若飞机上液压能源系统出现无流量输出的情况，维修人员就可根据此决策树查看相应的传感器的信息，首先查看压力传感器mP2的测量值以确定该故障是否是恒压液压泵的故障所导致的，如果压力传感器mP2所测的值为正常的2.8e7Pa，则排除了恒压液压泵的故障，接下来再查看压力传感器mP6的值以区分是负载(节流阀)的故障还是油箱3的故障。通过故障诊断决策树的应用可快速地对故障点进行隔离定位。

4 结论与展望

采用面向对象的建模语言Rodelica建立某飞机液压能源系统的行为模型，准确描述了飞机液压能源系统中各组件的正常行为以及故障行为。利用基于模型的故障诊断方法对所建模型进行分析，得出常见故障现象的诊断决策树，经验证所得决策树合理可靠，且具有工程实用性。

今后针对基于模型的故障诊断方法(系统)还可做以下几方面的研究:

1)目前实际系统与系统模型之间不存在实际的接口，所以在未来的工作中可以对该接口设计展开进一步的研究，以便实现动态的数据交互;

2)目前建立的系统定性模型都是采用离散化描述方式，难以处理随时间连续变化问题，即不能对动态系统进行建模。要实现系统的在线自主诊断，就需在动态系统建模方面有所突破。

［1］邵继业.基于模型的故障诊断方法研究及在航天中的应用［D］.哈尔滨:哈尔滨工业大学，2009.

［2］李伟.复杂系统的智能故障诊断技术现状及其发展趋势［J］.计算机仿真，2004，21(10):4 －7.

［3］Peter Bunus，Karin Lunde.Supporting model based diagnostics with equation-based object oriented languages［C］.2nd International Workshop on Equation-Based Object-Oriented Languages and Tools，Paphos，Cyprus，2008.

［4］Davis R.Diagnostic reasoning based on structure and behavior［J］.Artificial Intelligence，1984，24(1 － 3):347－410.

［5］Reiter R.A theory of diagnosis from first principles［J］.Artificial intelligence，1987，32(1):57 －96.

［6］Johan de Kleer，Williams BC.Diagnosing multiple faults［J］.Artificial Intelligence，1987，32(1):97 －130.

［7］Hofbaur MW，Williams BC.Hybrid estimation of complex systems［J］.IEEE Transactions on system，Man and Cybernetics B:Cybernetics，2004，34(5):2178 －2191.

［8］Hofbaur MW，Williams BC.Hybrid diagnosis with unknown behavioral modes［C］.Proceedings of the 13th International Workshop on PrinciplesofDiagnosis(DX02)，2002.

［9］Williams B C，Nayak P P.A model-based approach to reactie self-configuring system［C］.Procceeding of AAAI－96.1996.

［10］Bajwa A，Sweet A.The Livingstone model of a main propulsion system［C］.Proceedings of the IEEE，2003.

［11］欧阳丹彤，欧阳继红，刘大有.基于模型诊断的研究与新进展［J］.吉林大学自然科学学报，2001(2):38－46.

［12］Johan de Kleer，James Kurien.Fundamentals of modelbased Diagnosis［C］.IFAC Symposium Safeprocess，Washington USA，June，2003.

［13］Karin Lunde.Object-oriented modeling in model-based diagnosis［C］.In Proceedings of Modelica Workshop，Lund，Sweden，2000.