考虑弯曲刚度及边界约束的短索内力识别
陈舒婷 吴惠君 范中林 万 磊
(1.武汉理工大学交通学院 武汉 430063;2.湖北路桥集团有限公司 武汉 430044;3.十堰市公路管理局 十堰 442000)
斜拉索/吊杆是桥梁结构的主要受力构件,在对其进行的内力测试中,常规的索力识别公式存在以下问题:①未能考虑到抗弯刚度对索力的影响;②拉索的任何边界皆被视为铰支约束;③拉索长度没能准确给定[1-3]。对于长度较短的拉索,其弯曲刚度和边界约束对内力的识别结果影响甚大[4]。鉴于上述原因,针对工程中短索内力的识别问题,本文在同时考虑其弯曲刚度及边界约束的条件下,提出了等效长度的概念,从而可获得较为简单实用的拉索内力识别技术。
1 短索内力识别公式
1.1 频率方程
忽略拉索垂度的影响,引入考虑弯曲刚度及边界约束的拉索频率方程[5]。在两端固支和一端固支一端铰支约束下,拉索的频率方程分别为
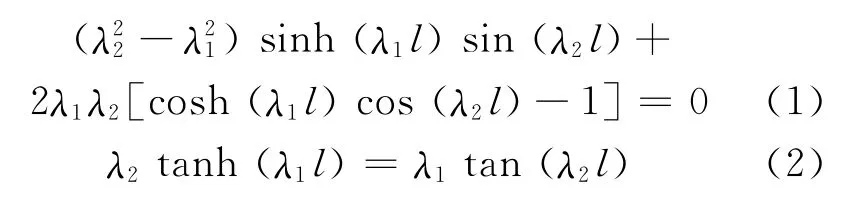
式中:
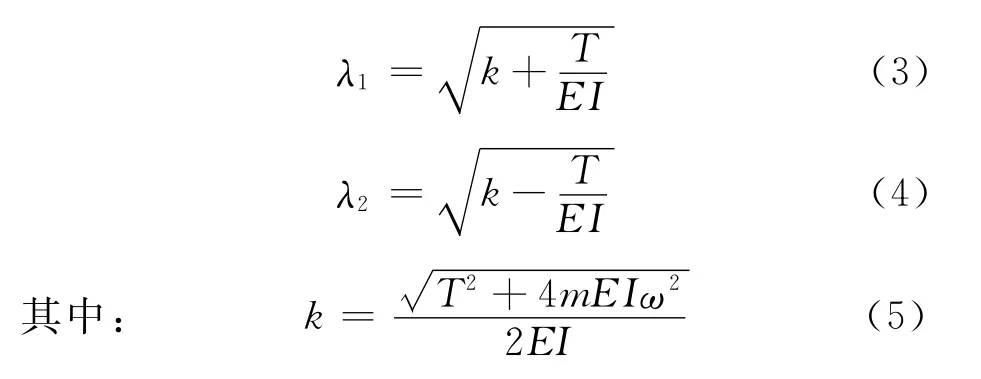
式(1)和式(2)为超越方程,求解较为复杂。
1.2 内力识别公式推导
现通过引入等效计算长度li(i为对应模态阶数),其为不同边界约束下对应的拉索计算长度,来解决特殊边界下拉索内力的识别问题。记拉索实际长度为l,等效长度为li,代入两端铰支约束下的拉索的振动频率公式,得到
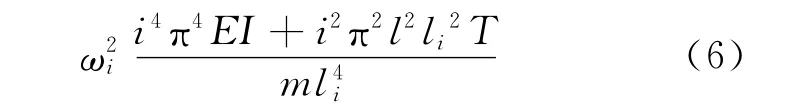
引入参数[6]
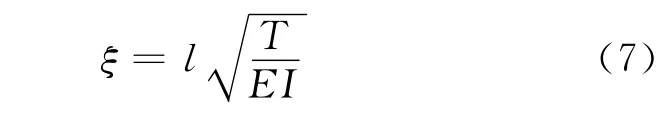
同时,令
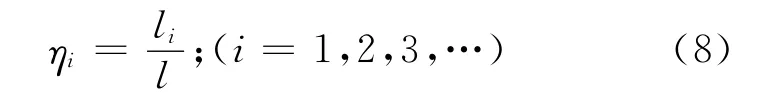
将式(6)、(7)及式(8)带入式(3)、(4)及式(5)得到用ζ和ηi表示的λ1和λ2,再将λ1和λ2带入特殊边界下的频率方程,即可得到对应边界下ηi-ζ的关系,通过牛顿迭代法[7],得到的结果见图1和图2。
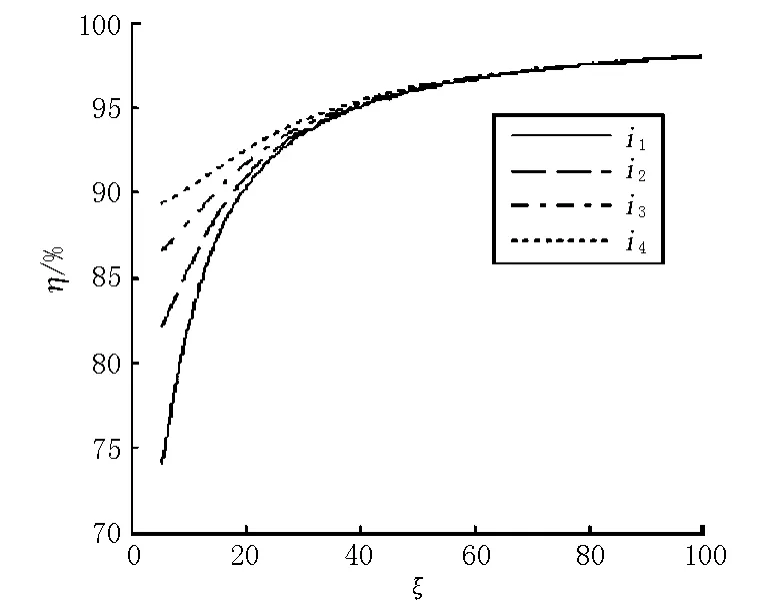
图1 两端固支约束下ηi-ζ关系
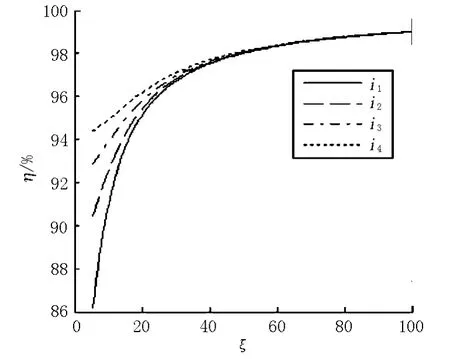
图2 一端固支一端铰支约束下ηi-ζ关系
曲线可分为4个阶段,而前4阶ηi-ζ关系趋势基本类似,将两者关系用分段直线ηi=k1ζ+k2来描述,而当ζ≥100时,曲线已基本平缓且ηi趋近于1,故此时可以按照两端铰支进行计算。通过最小二乘法处理以上数据,得到公式见表1~6。

表1 两端固支5.5≤ξ<15时ηi-ξ关系系数表
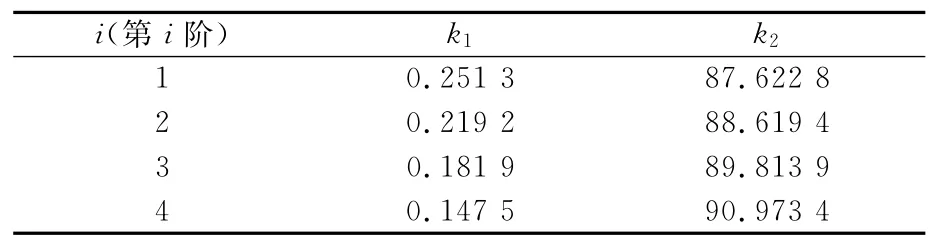
表2 两端固支15≤ξ<45时ηi-ξ时关系系数表

表3 两端固支45≤ξ<100时ηi-ξ时关系系数表

表4 一端固支一端铰支5.5≤ξ<20时ηi-ξ时关系系数表
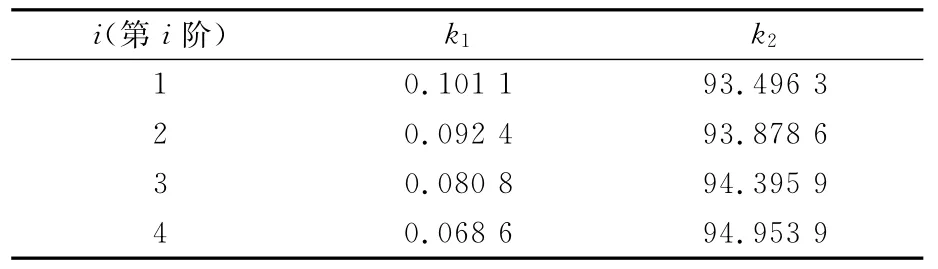
表5 一端固支一端铰支20≤ξ<45时ηi-ξ时关系系数表

表6 一端固支一端铰支45≤ξ<100时ηi-ξ时关系系数表
以前2阶频率ω1和ω2计算,由式(6)得到T和EI,利用ωi=2πfi及式(8),得到

这样,在已知边界约束、设计索力、索实际长度、截面参数、实测频率等条件下,迭代2~3次即可得到较为精确的拉索内力值及抗弯刚度EI。
2 数值模拟有效性验证
为了验证该方法对于识别拉索或吊杆的内力及弯曲刚度的有效性,通过数值模拟检验。
2.1 数值模拟的吊杆参数
现取长度分别为2,4,6和8m的吊杆,单位长度质量均为27.48kg/m,f1,f2分别为通过有限元方法计算得到的吊杆前2阶自振频率。各参数见表7。

表7 数值模拟的吊杆参数
2.2 等效长度方法的收敛及有效性验证
通过式(7)、(9)及式(10)迭代2~3次即可收敛。得到的结果见表8。
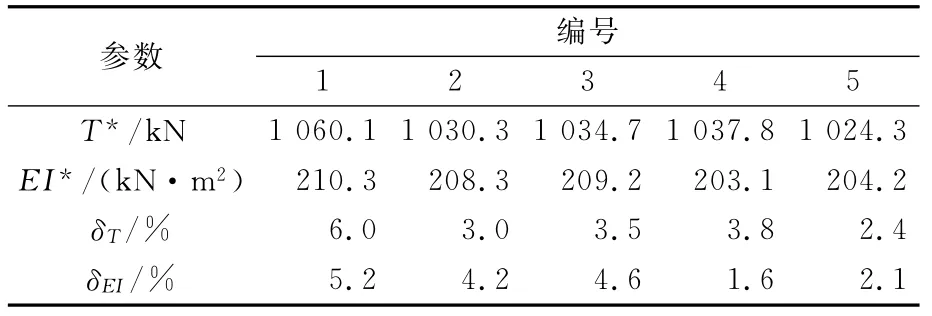
表8 数值模拟参数识别
表中T*和EI*为通过该方法识别的吊杆内力及弯曲刚度;δT和δEI为索力及刚度识别相对误差。从表8数据可以看出,由此方法进行的数值模拟参数识别收敛得较快,也具有一定的精度。
3 工程实例验证
本章以某钢管混凝土大桥检测数据为试验依据,取高强钢丝面积为2 706.62mm2,套管面积为1 649.33mm2,内充砂 浆面积 为 5 144.35 mm2,吊杆线密度为39.14kg/m,吊杆设计内力为780kN。以其中11,12,13,14号杆为研究对象,各参数见表9。
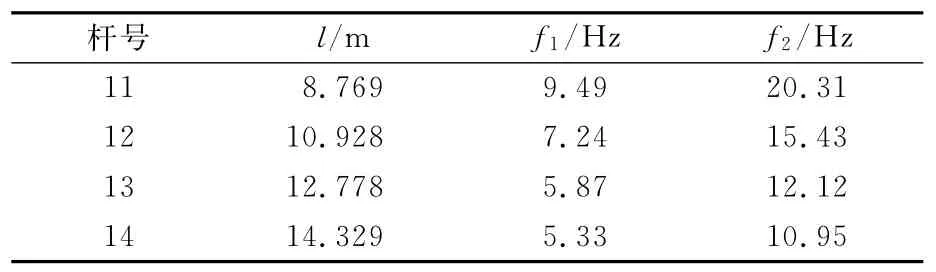
表9 吊杆杆长及实测频率
通过等效长度方法对吊杆内力及弯曲刚度进行识别,并同油压千斤顶读数进行比较,结果见表10。

表10 吊杆张拉力及弯曲刚度
从表10数据可以看出,该方法对于吊杆内力识别具有一定的精度,可为工程实用参考。
4 结语
针对工程中短索内力的识别问题,本文在同时考虑其弯曲刚度及边界约束的条件下,提出等效长度的概念,将拉索在两端固支以及一端固支一端铰支的边界约束下的索力识别,转换为拉索两端铰支约束下的索力识别问题,较为简单实用,可为工程实用参考。
(1)在给定边界约束,已知设计索力、索实际长度、截面参数、实测频率等条件下,利用式(7)求得对应的ξ,通过对应ηi-ξ关系求得对应等效长度,进而迭代2~3次即可得到较为精确的拉索内力值及抗弯刚度。
(2)利用本文提出的方法进行数值模拟,参数识别收敛得较快。同时,该方法对于短索内力识别具有一定的精度,可以一定程度上解决工程上短索内力识别的问题。
[1] 孟少平,杨 睿,王景全.一类精确考虑抗弯刚度影响的系杆拱桥索力测试新公式[J].公路交通科技,2008,25(6):87-98.
[2] 陈 淮,董建华.中、下承式拱桥吊索张力测定的振动法实用公式[J].中国公路学报,2007,20(3):66
[3] 王卫锋,韩大建.斜拉桥的索力测试及其参数识别.华南理工学学报:自然科学版.2001,29(1):18-21.
[4] 任伟新,陈 刚.由基频计算拉索拉力的实用公式[J].土木工程学报,2005,38(11):26-31.
[5] 孙良凤.短索张力和弯曲刚度的识别方法研究[D].杭州:浙江大学,2010.
[6] IRVINE H M,CAUGHY T K.The linear theory of free vibration of a suspended cable[J].Proceedings of Royal Society of London,Series A,1974,341:299-315.
[7] Z H,SHINKE T,NAMITA Y.Practical formulas for estimation of cable tension by vibration method[J].Journal of Structural Engineering,ASCE,1996,122(6):651-656.

