基于DSP的LoG边缘检测系统的设计与实现
宋伟中,朱卫东,杨洪涛
(中国人民解放军信息工程大学 河南 郑州 450001)
1 图像边缘检测算法
1.1 图像边缘
图像边缘定义为图像中相邻像素灰度具有阶跃变化或屋顶变化的那些像素的集合。根据灰度信号变化特点,边缘一般可分为阶跃状和屋顶状两大类[3],其特征如图1所示。
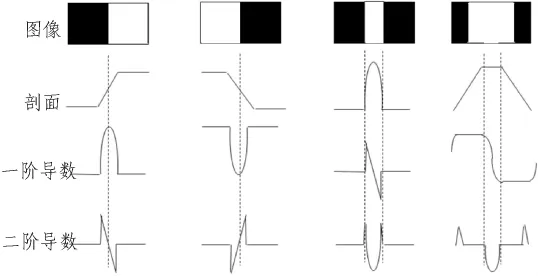
图1 图像边缘特征及其波形Fig.1 Image edge characteristics and waveform
可见,图像边缘的特征在于灰度信号的快速变化。对阶跃边缘,这种变化为跳变,其一阶导数在图像边缘位置处将产生一个尖脉冲,而其他位置都为0,这表明可用一阶导数的幅度值来检测边缘的存在。其二阶导数在一阶导数的阶跃上升区有一个向上的脉冲,而在一阶导数的阶跃下降区有一个向下的脉冲,在这两个脉冲之间有一个过0点,它的位置正对应原图像中边缘的位置,所以可用二阶导数的过0点检测边缘位置,而用二阶导数在过0点附近的符号确定边缘像素在图像边缘的暗区或明区。
对屋顶状边缘,屋顶状边缘的剖面可看作是将脉冲边缘底部展开得到,其波形变化为尖脉冲,所以它的一阶导数将产生上下两个脉冲,而它的二阶导数是将脉冲剖面二阶导数的上升沿和下降沿拉开得到的,通过检测屋顶状边缘剖面的一阶导数过0点,可以确定屋顶位置。
1.2 几种常用的边缘检测算子
基于一阶导数法的边缘检测算子的基本思想是:用一阶微分算子和图像卷积检测图像一阶导数的峰值或者谷值确定边缘,基于一阶导数法的边缘检测算子有梯度算子、Roberts算子、Prewitt算子、Sobel算子、Canny算子等。
基于二阶导数法的边缘检测算子的基本思想是:用二阶微分算子和图像卷积检测图像二阶导数的零点确定边缘,并可通过二阶导数的正负判断像素在明区还是暗区。基于二阶导数法的边缘检测算子有Laplacian(LoG)算子、Marr算子等。另外还有基于能量最小化准则的全局提取图像边缘方法、神经网络法和现代信号处理技术中的小波变换多尺度分析的图像边缘提取方法和基于小波包分解的图像边缘提取算法[4]。
1.3 Laplacian of Gaussian(LoG)算子
边缘检测离不开检测信号突变的基本思路,这会导致算法对噪声敏感,从而影响其检测效果。梯度算子只计算相邻像素的灰度差值,所以对噪声比较敏感且无法抑制噪声的影响;Roberts算子利用局部差分算子寻找边缘,定位比较准确,对噪声敏感,但是较梯度算子效果略好;Prewitt算子是一种边缘样板算子,在检测边缘的同时,能抑制噪声的影响;Sobel算子对像素4邻域采用带权方法计算差分,噪声抑制好,但是检测的边缘较宽;Kirsch算子在保持细节和抗噪声方面都有较好的效果,但其得到的图像边缘存在连续性较差的问题[5];拉普拉斯算子对细线和孤立点检测效果较好,但对噪音的敏感,不能检测出边的方向;Marr算子是在Laplacian算子的基础上实现的,Marr算子的平滑性质能够减少噪声的影响,故Marr算子也称为LoG (Laplacian of Gaussian)算子。Canny算子是一阶算子,其实质是用一个准高斯函数作平滑运算 fs=f(x,y)×G(x,y),然后以带方向的一阶微分算子定位导数最大值。
利用图像强度二阶导数的零交叉点来求边缘点的算法对噪声十分敏感,所以,希望在边缘增强前滤除噪声。为此,Marr和Hildreth将高斯滤波和拉普拉斯边缘检测结合在一起,形成 LoG(Laplacian of Gaussian, LoG)算法,也称之为拉普拉斯高斯算法或Marr算法。它是在Laplacian算子的基础上实现的,它得益于对人的视觉机理的研究,有一定的生物学和生理学意义。由于Laplacian算子对噪声比较敏感,为了减少噪声影响,可先对图像进行平滑,然后再用Laplacian算子检测边缘。LoG边缘检测器的基本特征是:
教学方法是否有效不仅决定了视觉传达设计教学质量的高低,而且决定了学生是否能适应新媒体时代对视觉传达设计提出的新要求。培养综合型的应用人才需要改进传统教学方法,不断根据新的内容创新教学形式,能够有效提高视觉传达设计教学质量,满足学生的学习需求。
1)平滑滤波器是高斯滤波器;
2)增强步骤采用二阶导数(二维拉普拉斯函数);
3)边缘检测判据是二阶导数零交叉点并对应一阶导数的较大峰值;
4)使用线性内插方法在子像素分辨率水平上估计边缘的位置。
这种方法的特点是图像首先与高斯滤波器进行卷积,这一步既平滑了图像又降低了噪声,孤立的噪声点和较小的结构组织将被滤除。由于平滑会导致边缘的延展,因此边缘检测器只考虑那些具有局部梯度最大值的点为边缘点。这一点可以用二阶导数的零交叉点来实现。拉普拉斯函数用作二维二阶导数的近似,是因为它是一种无方向算子。为了避免检测出非显著边缘,应选择一阶导数大于某一阈值的零交叉点作为边缘点。
平滑函数应能反映不同远近的周围点对给定像素具有不同的平滑作用,因此,平滑函数采用正态分布的高斯函数,即:

其中 σ 是方差。 用 h(x,y)对图像 f(x,y)的平滑可表示为:

*代表卷积。令r是离原点的径向距离,即r2=x2+y2。对图像 g(x,y)采用 Laplacian算子进行边缘检测,可得:
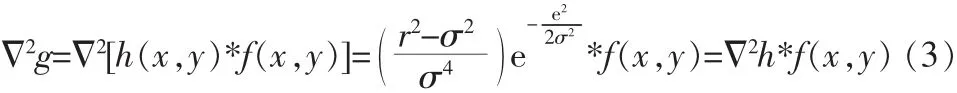
这样,利用二阶导数算子过零点的性质,可确定图像中阶跃边缘的位置。
由于的平滑性质Δ能减少噪声的影响,所以当边缘模糊或噪声较大时,利用2h检测过零点能提供较可靠的边缘位置。在该算子中,σ的选择很重要,σ小时边缘位置精度高,但边缘细节变化多;σ大时平滑作用大,但细节损失大,边缘点定位精度低。应根据噪声水平和边缘点定位精度要求适当选取σ。下面是σ=5时,Marr算子的模板:

图 2 Marr算子的模板(σ=5)Fig.2 Marr operator template(σ=5)
定义数字形式的拉普拉斯的基本要求是,作用于中心像素的系数是一个负数,而且其周围像素的系数为正数,系数之和必为0。但是Marr算子存在编程复杂、计算量大的缺点。本文利用TMS320DM642DSP(DM642)芯片高速运算能力的特点,在基于DM642的图像处理系统上实现了图像的边缘检测并取得了较好的边缘检测效果。
2 数字视频处理系统中Marr算子的实现
TMS320DM642是基于C64x内核的高速数字信号处理器,其时钟频率为600 MHz,最高可达720 MHz,这使得DM642在数字视频处理方面有着强大的优势,成为数字多媒体处理与应用的极好选择[7]。
2.1 基于DM642视频处理系统的硬件组成
基于DM642的视频处理系统组成如图3所示。
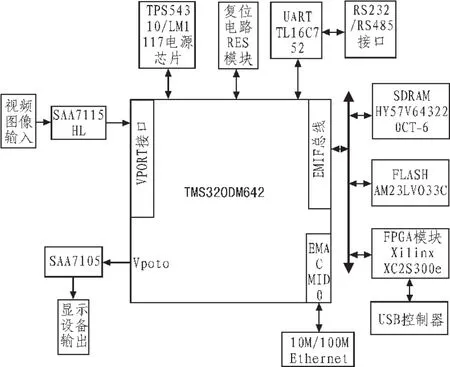
图3 图像处理系统的硬件框图Fig.3 Hardware diagram of video processing system
整个系统包括视频采集部分、信号处理部分(DM642)、传输部分及显示等单元。系统的工作流程是:系统上电或复位后,从Flash加载程序对芯片进行初始化和对外围硬件进行配置,DM642通过I2C总线对其它芯片进行控制,开始对图像进行采集,从CCD摄像头采集到的模拟视频信号经视频解码器SAA7115HL进行A/D转换为数字视频信号,送入DM642的VP端口,采集到的视频数据经EMIF存入SDRAM中,同时DM642对采集到的图像进行边缘检测处理,并把处理后的数据通过McBSP送入缓冲器中。
在显示操作期间,数据从存储器加载到帧缓冲器中,然后通过EDMA传输给视频端口FIFO,视频端口再将数据传输至视频编码器SAA7105,由SAA7105将数字视频信号转换为模拟的PAL制式或NTSC制式视频通过监视器等显示设备进行显示。
2.2 Marr算子边缘检测实现流程
当视频数据经EMIF存入SDRAM中后,由DM642对图像数据进行Marr边缘检测算法处理,算法的具体实现流程为[8]:
step1:建立高斯滤波矩阵减去元素的平均值,进行图像的平滑处理,滤去噪声;
step2:再用刚得到的值进行卷积运算来增强边缘,然后设置阈值,得到过零点的设为1,其余的设为0,得到新的而至图像的矩阵;
step3:Gaussian平滑函数平滑后输出图像;图4给出了系统的具体实现流程;
3 实验结果
为检验上述系统的有效性,以640×480的256色实验台灰度图像为测试对象,选用σ=5的5×5的Marr算子模板进行测试,图5和图6给出了本系统下采集到的图像与经过Marr算子边缘检测后的结果。由实验结果可知,经Marr边缘检测算子处理能很好的抑制噪声和虚假边缘,检测到的边界轮廓清晰,有较高的边缘精度。
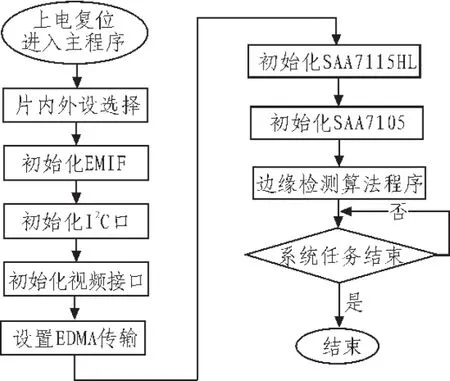
图4 DM642数字图像处理系统程序流程Fig.4 DM642 digital image processing system processes
图5 原始图像Fig.5 Original image

图6 Marr边缘检测Fig.6 Edge detection
4 结束语
边缘检测在数字视频监控、模式识别、机器视觉等领域都有重要应用,文中讨论了边缘检测的原理,对几种重要的检测算法进行了分析比较,重点分析了Marr算子的原理及其实现过程,并基于TMS320DM642数字视频处理系统实现了Marr算子的边缘检测任务,实验结果表明提取的边缘较为完整,细节表现明晰,边缘的连续件也很好,具有良好的边缘检测效果;对数字视频监控、智能目标检测的进一步应用提供了有价值的借鉴。
[1]Babu R V,Makur A.Object-based surveillance video compression using foreground motion compensation[J].ICARCV′06,2006:1-6.
[2]Marrand D,Hildreth E.Theory of edge detection[J].Proc.RSoc London,Set B.207,1980:187-2170.
[3]黄爱民,安向京,骆力.数字图像处理及分析基础[M].北京:中国水利水电出版社,2005.
[4]竺子民.光电图象处理[M].武汉:华中理工大学出版社,2001.
[5]ZHAI Lei,DONG Shou-ping,MA Hong-lian.Recent methods and applications on image edge detection[J].International Workshop on ETT and GRS 2008(1):332-335.
[6]Otsu N.A threshold selection method from gray-level histograms[J].IEEE Trans on systems,Man,and Cybernetics,1979,9(1):50-69.
[7]TEXAS INSTRUMENTS TMS320DM642 Video/Imaging Fixed-Point Digital Signal Processor[EB/OL]. (2005).Http://www.ti.com.
[8]Clark J J.Authenticating edges produced by zero-crossing algorithms[J].IEEE Trans,1989(6):43-57.

