一种改进蚁群优化算法的仿真研究

张 毅 高永琪 牛兴江

（海军工程大学兵器工程系 武汉 430033）

0 引 言

路径规划［1－2］是指在特定的约束条件下，如在综合考虑机器人（航行器）的到达时间、燃料消耗、威胁，以及飞行区域的选择等因素的前提下，为机器人（航行器）规划出一条最优的，或者满足特定需要的行走路径，从而保证圆满完成任务．

传统的路径规划算法主要有最速下降法［3］、A＊算法［4］、图搜索算法［5］等，由于路径规划问题属于组合优化问题，基本都是 NP－Hard问题［6］，因此传统路径规划方法都存在不同程度上的不足．而研究表明，一些生物启发式算法在解决NPHard问题时，往往能够取得更好的结果，比如，粒子群算法、遗传算法、鱼群算法，以及蚁群优化算法等．其中蚁群优化算法在解决旅行商问题（traveling salesman problem，TSP）、机器人路径规划等组合优化问题中取得了较其他方法更优的结果．但是蚁群优化算法也存在容易陷入局部最优、收敛速度慢、参数设置麻烦等不足［7］．本文针对蚁群优化算法的上述缺点进行了改进研究，并对TSP问题和机器人路径规划问题进行了仿真研究和比较．

1 蚁群算法

蚁群优化算法（ant colony optimization，ACO）［8－9］针对离散的组合优化问题，采用概率性选择机制并正向移动地构建解，信息素的更新是在逆向移动中做出，信息素的释放量和之前构建解的质量有关．为了更好地探索最优解，算法加入了信息素挥发机制．

下面以求解平面上N个城市的TSP问题为例来说明蚁群算法的状态转移规则［10－11］．设m为蚂蚁数量，dij（i，j＝1，2，…，n）表示城市i和城市j之间的距离，τij（t）表示t时刻在ij连线上残留的信息素．蚂蚁k（k＝1，2，…，m）在运动过程中根据各路径上的信息量决定转移方向．蚂蚁系统所使用的状态转移规则被称为随机比例规则，其给出了位于城市i的蚂蚁k选择移动到城市j的概率．在t时刻，蚂蚁k在城市i选择城市j的转移概率（t）为

式中：allowedk为蚂蚁k下一步允许选择的城市集合；ηij为启发式函数；α和β为2个参数，分别反映了蚂蚁在运动过程中所积累的信息和启发式信息在蚂蚁选择路径中的相对重要性．

蚂蚁根据式（2）所给出的伪随机比例规则移动到下一城市

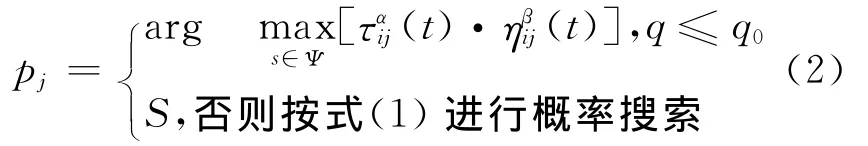
式中：q为［0，1］区间均匀分布的随机数；q0（0≤q0≤1）为参数；S为根据式（1）给出的概率分布所选出的为随机变量．

当蚂蚁完成一次循环，各路径上信息素根据下式调整．

式中：Δτkij（t，t＋1）为第k只蚂蚁在时刻（t，t＋1）留在路径ij上的信息素；Δτij（t，t＋1）为本次循环中路径ij上信息素的增量；ρ（0＜ρ＜1）为信息素的挥发系数．

2 算法改进

由于蚁群优化算法存在容易陷入局部最优、计算量大、没有明确的参数设置方式等缺点，本文对蚁群优化算法做如下改进．

1）蚁群算法在构造解的过程中，利用了概率随机选择的策略，这使得算法的收敛速度慢．式（2）中的参数q0对于算法的选择策略起着关键性的作用，因此本文对q0的取值进行了改进．随着搜索的进行，动态地调整q0的值

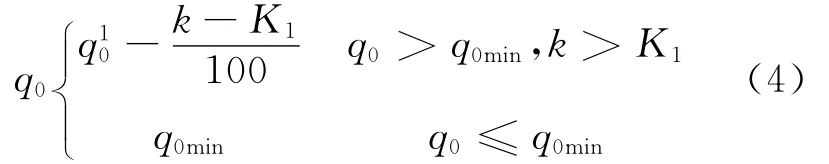
式中：k为当前搜索的次数；K1为一具体的搜索次数；q10（q0min≤q10≤1）为q0的一个较大的初始值；q0min为q0的下限．

初始时刻定义较大的q0能够加快算法的收敛速度，当搜索到一定代数K1后，搜索方向已经基本确定，这时减小q0的值，能够适当加大随机选择的概率，即是在前K1次迭代所搜索的最好解周围加强了局部搜索的能力．这一改进减小了路径选择的计算量，不仅能够加快收敛速度，节省搜索时间，而且能够克服算法过早的停滞，有利于发现更好的解．

2）为了避免搜索的过早停滞，借鉴最大－最小蚂蚁系统的方法，将信息素的值域范围限制在［τmin，τmax］区间内，并且将信息素轨迹初始化为

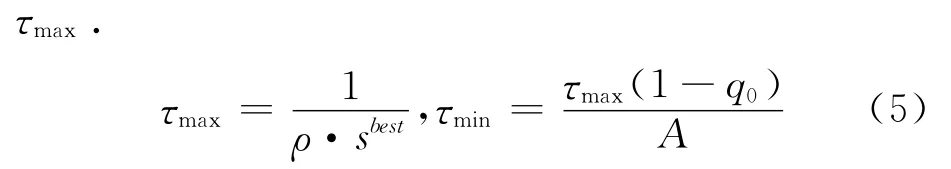
又算法的信息素更新规则为

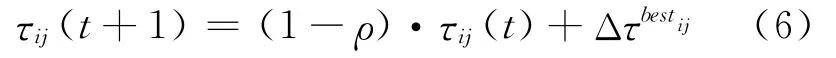
式中：Δτbestij ＝1／f（sbest），f（sbest）为当前迭代最优解sib或者全局最优解sgb．为了兼顾收敛速度和解搜索范围，蚂蚁在搜索过程中默认使用sib进行信息素更新，只在第10n（n＝1，2，…）次循环中使用sgb．

3）当所有蚂蚁完成一次循环，只有本次迭代构造出最优解和最差解的蚂蚁才被允许释放信息素．其中最优解路径上的信息素更新公式如式（6）所示，对于最差解所经过的路径ij，并且ij不属于最优解，则ij上的信息素更新公式如下．

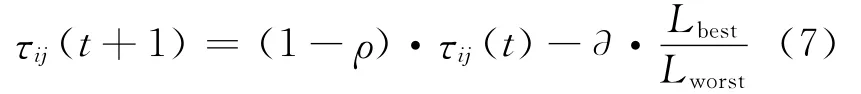
式中：∂为一个固定的参数；Lbest为本次迭代中最优路径长度；Lworst为本次迭代中最差路径长度．

这样的改进能够对最优解进行更大限度的增强，并且对最差解进行消弱，使得最优路径与最差路径之间的信息素差异进一步增大，从而使蚂蚁的搜索行为能够更加集中于最优解附近．

3 仿真研究

3．1 TSP问题

以中国大陆31个省会、自治区和直辖市城市的相对坐标为基础的TSP问题为例，利用Matlab 7．0对改进算法和基本蚁群优化算法进行20次仿真实验．算法的各参数设置见表1．

表1 系数取值

以纬度方向为X轴，经度方向为Y轴建立31个城市的相对位置坐标系，仿真结果分别见表2和图1．

表2 仿真结果对比

由以上仿真结果可知，改进的算法在解决TSP问题时，不仅能够得到更好的解，更能显著地提高算法的收敛速度．

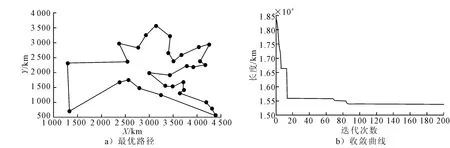
图1 改进算法所得到的最好解

3．2 机器人路径规划问题

首先对环境进行网格化处理，网格长度为1，障碍物（威胁）用圆形区域表示（如图2）．不同于TSP问题中的信息素表示方式，这里将信息素存储在环境模型的离散点上，每个点上信息素的大小代表该离散点对蚂蚁的吸引程度．

算法的参数设置见表3．仿真结果见图3．

表3 系数取值

图2 规划路径

图3 收敛曲线

图3 分别为改进算法和基本蚁群优化算法的历次迭代最小路径长度，即收敛曲线，通过对比可知，改进算法能够显著提高算法的收敛速度．

4 结束语

蚁群优化算法是模拟自然界中的蚂蚁觅食过程可以找到最短路径的行为过程而设计的一种仿生算法，作为通用型随机优化方法，它吸收了蚂蚁的行为特性，通过其内在的搜索机制，利用一群人工蚂蚁的协作来寻找问题的解，成为求解组合优化等NP－Hard问题的一种有效的智能优化算法．然而蚁群算法存在容易陷入局部最优、收敛速度慢、参数设置麻烦等不足．本文对蚁群算法的上述问题进行了改进，并对TSP问题和路径规划问题进行了仿真研究．仿真结果表明：改进之后的算法不仅能够得到更好的解，更能显著地提高算法的

收敛速度．

［1］谢晓方，孙 涛，欧阳中辉．反舰导弹航路规划技术［M］．北京：国防工业出版社，2010．

［2］樊晓平，罗 熊，易 晟，等．复杂环境下基于蚁群优化算法的机器人路径规划［J］．控制与决策，2004，19（2）：166－170．

［3］韩志刚，林争辉，李林森，等．低空突防路径规划方法综述［J］．飞行力学，2002，20（3）：1－4．

［4］顾新艳，金世俊．基于A＊算法的移动机器人路径规划［J］．科技信息：科学教研，2007，34：36－38．

［5］仝秋红，赵忠杰．汽车驾驶智能化中路线规划及导航的最佳路径求解法［J］．西安公路交通大学学报，1999，19（3）：88－90．

［6］温一慧．组合·算法·理论与应用［M］．兰州：兰州大学出版社，2006．

［7］DORIGO M，GAMBARDELLA L M．Ant colony system：a cooperative learning approach to the traveling salesman problem［J］．IEEE Transactions on Evolutionary Computation（S1089－778X），1997，1（1）：53－66．

［8］COLORNI A．Ant system for Job－shop scheduling［J］．JORBEL，1994，34（1）：39－54．

［9］DORIGO M，STUTZLE T．Ant colony optimization［M］．Brussels：MIT，2004．

［10］李士勇．蚁群算法及其应用［M］．哈尔滨：哈尔滨工业大学出版社，2004．

［11］彭斯俊，黄樟灿，刘道海，等．基于蚂蚁系统的TSP问题的新算法［J］．武汉汽车工业大学学报，1998，20（5）：88－92．