逐差法和Origin8.0软件在牛顿环实验数据处理中的比较*

唐春红 唐曙光 刘扬正

(南京工程学院基础部 江苏 南京 210067)

1 引言

逐差法是物理实验中常用的数据处理方法之一，尤其在处理一系列等间距依次变化的测量数据时，把所有数据分成前、后两组再将对应项相减，既充分利用了所有测量数据，又具有对数据取平均和减少相对误差的效果，在研究数据与应变量之间的函数关系时有其独特的优点，但该数据处理方法往往非常费时，且容易出错．随着现代教育的发展，大量的实验数据和图像都可以通过计算机应用软件进行分析和处理，能使学生从繁琐的数据推导和计算中解脱出来，提高了学生的学习效率．简单易学、操作灵活、功能强大的Origin8.0软件在教学、科研、工程技术领域有非常广泛的应用[1]，在大学物理实验中适当地介绍这种基于Window平台的数据分析和图形可视化绘图软件，对于学生后续数据处理能力的培养起到一个抛砖引玉的作用．

本文以Origin8.0软件用于牛顿环实验数据处理为例，并与逐差法进行比较，使用Origin8.0软件能快速处理与分析实验数据．

2 实验原理

图1 等厚干涉条纹-牛顿环

很难准确判定各干涉条纹的级次，为此在实验中一般采用k测级圆环的直径Dk和k+m级干涉圆环的直径Dk+m，则

有

所以

只要测出Dk和Dk+m，知道级差，并已知光的波长λ，便可计算R．

3 实验数据及处理结果比较

3.1 实验数据

本实验原始数据来源于教师的备课，数据及部分数据处理见表1.

表1 牛顿环测量数据m=10,λ=5.893×10-4mm

3.2 逐差法处理实验数据

逐差法处理实验数据一般来说要求满足两个条件：

(1)函数具有的线性y=kx+b或者有多项形式；

(2)自变量是等间距变化．本实验教材上采用逐差法处理实验数据[2]．

用逐差法求R及R不确定度的计算．

21.031+21.035+21.017) mm2=21.021 mm2

逐差法处理实验数据的结果是

R=(891.8±3.976) mm≈(892±4) mm

相对不确定度为

3.3 Origin8.0处理实验数据[3]

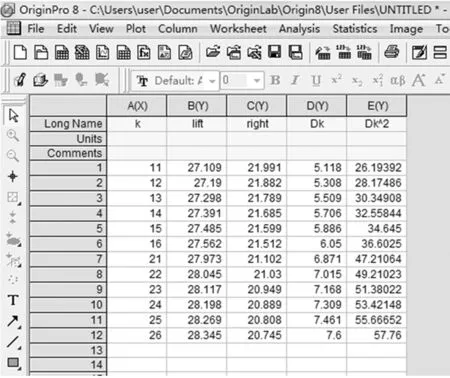
图2 Origin工作表

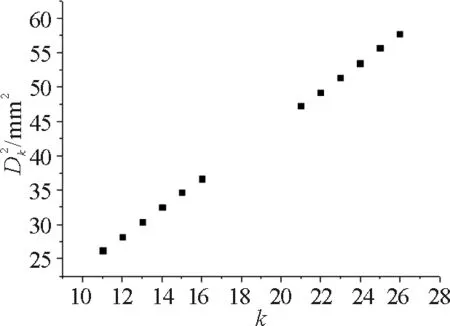
图3 k-散点图

拟合直线：绘出散点图后，选择Analysis菜单中的Fit Linear，即可对图1进行线性拟合，Graph1中新增一条拟合出来的直线，见图4，同时弹出结果窗口Results Log，显示拟合结果．

图4 线性拟合图

图4中左上角点表示数据散点图，线表示拟合的直线，右下角为弹出的结果窗口，即为拟合的参数，拟合参数见图5.

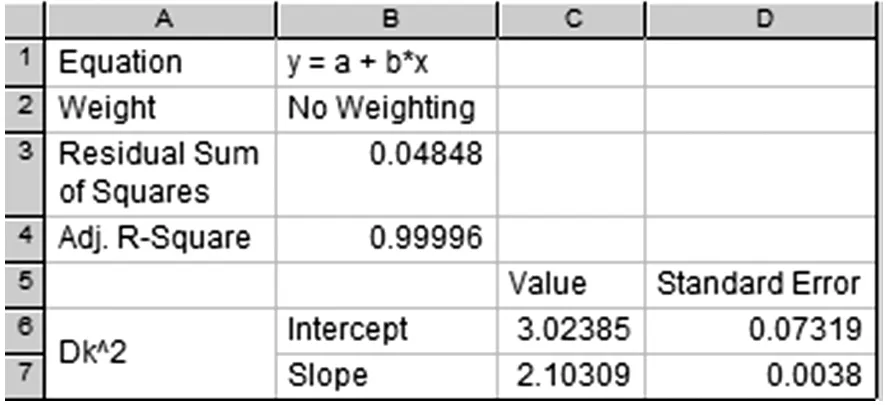
图5 拟合参数

从图5可以看出，直线的回归方程y=a+bx，参数a和b分别为截距、斜率．由Results Log窗口信息可知拟合直线的截距为a=3.023 85，其标准差为0.073 19，斜率为b= 2.103 09, 标准差为0.003 8，线性拟合相关常数R=0.999 6，说明所测量的数据其拟合直线几乎全部通过数据点．

Origin8.0处理实验数据的结果是：

由方程4Rλ=b=2.103 09得R=892.2 mm，标准偏差为0.048 48 mm，相对不确定度为ER=

0.38%．

3.4 两种数据处理方法的结果比较

4 结论

通过Origin8.0软件处理用牛顿环实验数据，并与教材使用的逐差法处理实验数据进行比较，充分体现了用计算机软件处理实验数据简化了数据处理过程，提高了实验结果的准确度，也避免了人为因素(操作不规范等)所造成的误差，在物理实验数据处理过程中有显著的应用价值．

参考文献

1 李晓波 ，谢志远．Origin作图在大学物理实验教学中的应用及评价. 襄樊学院学报,2010(8):86～88

2 唐曙光．大学物理实验.北京：科学出版社，2011.126～130

3 王晓雄．利用Origin拟合方法处理牛顿环实验数据，大学物理实验，2011(4):73～74