全站仪免置平自由设站及其测量方法
朱洪涛,徐宜敏,吴维军,2
(1.南昌大学机电工程学院,南昌 330031;2.江西日月明铁道设备开发有限公司,南昌 330029)
工程测量时,全站仪需在测量前先行设站以确定全站仪的自身位置,即站点坐标。全站仪设站的首要工作是将全站仪精密置平,电子气泡居中,使全站仪内部平面坐标系X-Y与大地坐标系中的水准平面X′-Y′平行。在置平状态下,可通过内置算法把斜距、水平角及垂直角(通常采用天顶距法)等测量信息映射到大地坐标系中。当全站仪设站不满足置平要求,将导致测量成果偏离真值。以准确度等级为Ⅱ级的全站仪为例,当斜距为100 m,水平偏差为0.001°条件下,其点位误差可达1.74 mm。因此全站仪正确设站和测量的先决条件是全站仪必须处于置平状态。
全站仪的精密置平需要人工完成,其置平效果很大程度上依赖于操作者的经验与技能。我国的高速铁路无砟轨道平顺性主要是通过各级精测网联测进行控制[1],其设站间距为60~120 m[2]。频繁换站并置平将降低测量作业效率,增加人力和时间成本。研究全站仪在非置平状态下的自由设站和三维测量技术,对于充分发挥全站仪的作用,提高全站仪的使用效能,保证高速铁路运营的安全性、舒适性,具有显著的理论和现实意义。
1 全站仪免置平自由设站
全站仪自由设站的实质是后方交会,因置站于非已知点,站点位置的选择比较自由而得名,它通过对2个及以上已知点的联测,快速确定设站点坐标[3];在此基础上,以设站点为已知点,对待测点进行测量[4]。
如前所述,由于全站仪在置平状态下其内部坐标系X-Y平面与大地水准平面X′-Y′平行,此时测量得到的水平角和天顶距都是以大地水准平面为参考水平面。全站仪在非置平状态下直接测量得到的水平角和天顶距是基于其内部坐标系X-Y平面,由于全站仪内部坐标系X-Y平面与大地水准平面X′-Y′之间存在夹角,全站仪在置平和非置平状态下测量得到的水平角和天顶距是不同的。传统的一边一角后方交会,双边单角后方交会等自由设站方法[5]都是以全站仪置平为前提的,这些设站算法及其测量方法在非置平状态下将不再适用。
1.1 全站仪免置平自由设站站点坐标计算模型
根据全站仪测距原理可知,无论全站仪在置平或者非置平状态下,斜距测量精度基本相当。所以全站仪在非置平状态下完成自由设站,要充分利用全站仪在非置平状态下的斜距测量信息。
如图1所示,设已知基准点P1、P2、P3的大地坐标分别为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3),并已知全站仪站点P与各基准点的斜距分别为s1、s2、s3,设全站仪站点P在大地坐标系上的坐标为(x0,y0,z0),则有方程
(1)
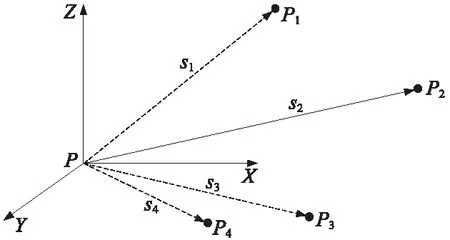
图1 全站仪自由设站示意
1.2 全站仪免置平自由设站的多值问题
可通过解析方法或数值计算方法求解非线性方程组(1)。由于非线性方程组(1)中每个方程关于未知量x0,y0,z0的结构形式相同,只有x1,y1,z1,s1…x3,y3,z3,s3等常量不同,所以可以通过消元法进行求解,即使相邻的2个方程相减消去方程组中次数为二次的未知量。
由于方程组(1)是三元二次方程组,所以方程组(1)可能存在多解问题。最简单的方法是通过第4个大地基准点P4(x4,y4,z4)进行如下判断:根据第4个大地基准点P4的坐标与方程组的某个解,反算第4个大地基准点与全站仪站点之间的距离,与实际测量得到的距离s4进行比较,如果反算得到的距离与测量得到的距离s4相等或者误差在一定范围内,则认为该组解就是全站仪的站点坐标P(x0,y0,z0)。如果反算得到的距离与测量得到的距离s4误差超差,则认为该组解不是设站点坐标,将该解剔除。如果可利用的大地基准点多于4个,可通过全站仪对多余的基准点进行多余测量,通过平差计算[6]以提高全站仪设站的站点坐标精度。
在选择第4个基准点有困难的情况下,可充分利用全站仪免置平测量方法中的方向余弦矩阵,方向余弦矩阵中的元素为全站仪坐标轴X轴、Y轴、Z轴在大地坐标系中的方向余弦。在实际工程测量中,全站仪即使没有置平其坐标轴Z轴的正方向始终是朝上,不会指向地面,即全站仪坐标轴Z轴的正方向与大地坐标系的Z′轴的正方向的夹角小于90°,即全站仪坐标轴Z轴的正方向与大地坐标系Z′轴的正方向的余弦值始终是大于零的。由(1)式解出全站仪设站点坐标的2个解是关于大地坐标系X′O′Y′平面对称的,必然存在1个解使得全站仪坐标轴Z轴的正方向与大地坐标系的Z′的正方向的余弦值大于零,一个小于零。即使得全站仪坐标轴Z轴的正方向与大地坐标系的Z′的正方向的余弦值小于零的解不是设站点坐标,大于零的解为设站点坐标。
2 全站仪免置平自由设站的测量算法
全站仪在非置平状态下,不能通过全站仪内置算法将待测点在全站仪内部坐标系中的测量成果映射到大地坐标系中,需重新设计全站仪免置平自由设站后的测量算法,即重新建立全站仪内部坐标系与大地坐标系之间的三维坐标转换模型。三维坐标转换模型有基于旋转角的非线性模型[7],四元素法[8],基于方向余弦矩阵等方法,本文采用基于方向余弦矩阵的三维坐标转换模型。
基于方向余弦矩阵的三维坐标系转换模型[9]见式(2)
(2)
其中,[X′Y′Z′]T为P点在大地坐标系X′Y′Z′中的坐标;[XYZ]T为其在全站仪内部坐标系XYZ中的坐标;[ΔXΔYΔZ]T为平移量;μ为尺度比;R为方向余弦矩阵。
其中方向余弦矩阵R中的元素由全站仪坐标轴X轴、Y轴、Z轴在大地坐标系中的方向余弦组成,(a10,a20,a30)为全站仪X轴在大地坐标系中的方向余弦,(a11,a21,a31)为全站仪Y轴在大地坐标系中的方向余弦,(a12,a22,a32)为全站仪Z轴在大地坐标系中的方向余弦。并且全站仪坐标系与大地坐标系的尺度比μ等于1。
则(2)式可以转换为
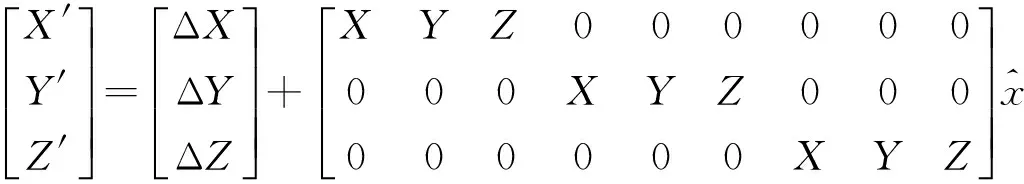
(3)
其中:


(4)
其中:

又因为R为正交矩阵,满足RRT=RTR=E,即矩阵R中的元素满足以下6个条件
(5)
式(5)表明矩阵R中的9个元素之间存在关系。由式(4)和式(5)构成附有限制条件的间接平差模型。对于只有2个或2个以下公共点,可以采用附有限制条件的间接平差模型[11]求解。在实际工程中至少都有3个或3个以上公共点,则可以直接采用以下最小二乘法形式进行求解,则有
(6)
当把式(3)中的12个待估参数求解出来之后,然后利用全站仪测量待测点得到待测点在全站仪坐标系统下的坐标[XYZ]T,代入(3)式,即可求得待测点在大地坐标系上的坐标[X′Y′Z′]T,完成全站仪在非置平状态下的工程测量。全站仪免置平自由设站及其测量算法中没有进行任何线性化处理,因此该方法适用于任意倾斜状态下的全站仪自由设站及其测量。
3 方法验证及数据测量
根据以上理论推导,采用VC++6.0编译软件编写程序代码,实现了功能,并采用Leica TPS1200系列全站仪等仪器进行实验。
实验环境如下。
温度:23~26 ℃;气压:1 011~1 012 hP;湿度:50%~60%;空气:有风(3~4级风速)。
仪器型号:Leica TCRP 1201+400;仪器精度:1′(测角);1+1.5 ppm(测距)。
实验方法如下。
在实验测量现场布设5个已知坐标的基准点,任取5个基准点中的4个作为已知坐标基准点,另一个基准点作为未知点,然后自由移动全站仪,让全站仪在每个站点进行免置平自由设站及其测量。其中,对式(1)采用消元法求解,对式(3)采用最小二乘法求解,得到全站仪的站点坐标和测量转换参数,然后对未知点进行测量。为分析测量重复性,实验中前后移动全站仪6次并分别进行设站和测量第5个点的坐标,然后通过式(3)把测量得到的全站仪内部坐标转换到大地坐标系上。实验数据见表1。

表1 对第5个基准点测量得到的全站仪坐标以及转换后的大地坐标 mm
根据表1所得的数据分别计算第5个点转换后所得大地坐标系中X、Y、Z的标准不确定度[12]。标准不确定度计算公式为
(7)

(8)

实验结果表明,免置平状态下测量精度与置平状态下测量精度相当,能够满足对大型建筑物精密测量的要求。
4 结语
本文研究的全站仪免置平自由设站及其测量方法,能够较好地克服目前全站仪设站及其测量只能在置平状态下进行的缺点。首先通过全站仪在非置平状态下测量至少3个大地基准点的斜距、水平角和天顶距,充分利用斜距信息建立自由设站模型,获得全站仪在大地坐标系上的站点坐标;其次,在非置平状态下完成自由设站之后,根据基于余弦矩阵的三维坐标系转换模型,通过最小二乘法进行求解,得到全站仪内部坐标系与大地坐标系之间的转换关系;最后,对待测点进行测量获得待测点的三维大地坐标。通过测量实验,表明本文所提出的全站仪免置平自由设站及其测量方法精度较高,可靠性好,同时算法原理简单,易于编程实现。全站仪免置平自由设站及其测量技术在保证精度的前提下,能够为建筑、水利等的工程测量及铁道建筑的精测节约成本、提高效率。
[1] 中华人民共和国铁道部.铁建设[2009]674号 高速铁路无砟轨道施工精调作业指南[S].北京:中国铁道出版社,2009.
[2] 李明领.高速铁路无砟轨道CPⅢ控制网建立与精度控制[J].铁道标准设计,2010(1):84-86.
[3] 王江,杨旭辉.全站仪在曲线测量中的应用[J].铁道标准设计,2002(11):14-17.
[4] 王庆,于先文.顾及已知点精度的自由设站算法及精度分析[J].东南大学学报:自然科学版,2009,39(2):372-376.
[5] 朱洪涛,吴维军.提高全站仪自由设站精度方法研究[J].铁道工程学报,2004(5):21-23.
[6] 王解先,高小兵,候东亚,等.高速铁路CPⅢ点整体三维严密平差[J].测绘通报,2011 (1):46-48.
[7] 曾文宪,陶本藻.三维坐标转换的非线性模型[J].武汉大学学报:信息科学版,2003,28(5):566-568.
[8] 滕志远,张爱武.单位四元素法在激光点云坐标转换中的应用[J].测绘通报,2011 (11):7-10.
[9] 陈义,沈中云,刘大杰.适用于大旋转角的三维基准转换的一种简便模型[J].武汉大学学报:信息科学版,2004,29(12):1101-1104.
[10] 陆钰,陈义,郑波.总体最小二乘法在三维坐标转换中的应用[J].大地测量与地球动力学,2008,28(5):77-80.
[11] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉大学出版社,2003.
[12] 张春富,张军,许文海,唐文彦.激光跟踪仪现场测量不确定度的评定[J].计量学报,2005,26(1):20-22.

