预应力钢束空间干涉快速计算方法

耿 杰

(中铁第四勘察设计院集团有限公司桥梁处,武汉 430063)

近年来，随着铁路建设大规模的开展，桥梁特殊结构比重大幅增加且设计周期越来越短。以混凝土箱梁而言，梁体几何形状趋于复杂，梁体内预应力钢束的布置也随之变得更加困难，出现了大量平纵弯重叠的情况；与此同时，斜腹板梁由于能够有效减小桥墩顶帽宽度，得到了广泛的应用，在这种情况下，由于腹板倾斜，预应力钢束的形状变得愈发复杂。因此，如何准确、快速判断钢束之间、钢束与普通钢筋之间以及钢束和梁体表面之间的距离是否满足规范要求成为了一个需求。本文通过建立预应力钢束的空间参数方程，运用数值计算方法求解钢束之间、钢束与梁体表面之间的最小间距，从而提高了设计效率，确保设计质量。

1 预应力钢束空间曲线方程

由于箱梁是纵向承载构件，预应力钢束的曲线方程在纵向上一般为单值函数。故以箱梁小里程方向的顶面中点为原点，以纵向为X轴，以横向为Y轴，按照右手法则建立空间坐标系。

工程上习惯用平面、立面投影来表达三维物体，在建立预应力钢束空间方程的时候，也借鉴了这种思路。将复杂三维形状拆分为2个平面图形，进而用参数方程来表达。对于预应力钢束而言，其投影图形一般由直线和圆弧组成，可用分段函数表达。如对于直线段而言，确定了起点和终点坐标之后(图1)，方程可表达如下

×(x-x0)+y0(1)

式中x0,y0——直线段起点坐标；

x1,y1——直线段终点坐标。

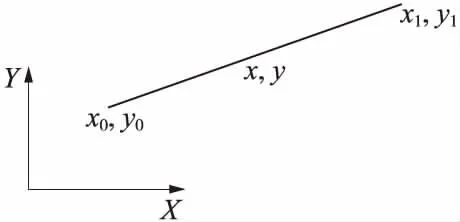
图1 直线段方程示意

对于圆弧段而言，考虑到圆弧两侧均有直线相切这一约束条件(图2)，方程可以表示如下

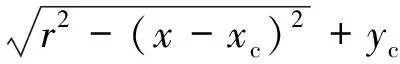
式中xc,yc——圆弧段圆心坐标；

y0——圆弧段起点Y坐标；

y1——圆弧段终点Y坐标；

ym——圆弧段中点Y坐标；

r——圆弧段半径。

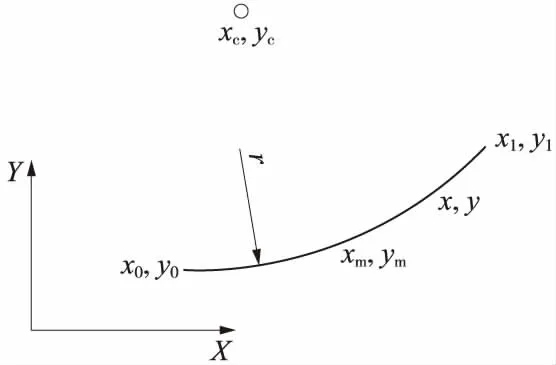
图2 圆弧段方程示意

对某一钢束立面(或平面)投影的二维平面方程可利用分段函数表达如下

X=x

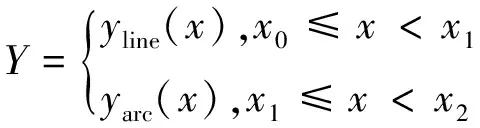
利用立面曲线表示预应力钢束到顶板(即XOY平面)的距离，用平面曲线表示钢束到截面中心(即XOZ平面)的距离。特别的，当钢束是腹板索时，考虑斜腹板的情况，平面曲线将表示钢束到腹板外侧的水平距离，在计算时需要做一次转换，如图3所示。

图3 预应力钢束空间模型

根据以上条件，建立预应力钢束空间曲线的参数方程

X=x

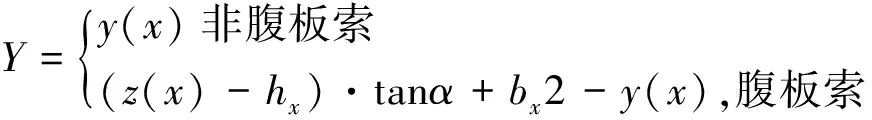
Z=z(x)

式中hx——x处的截面总高度；

α——腹板倾角，rad；

bx——x处的截面底宽。

于是，对于给定的x坐标，能够计算出对应的钢束空间位置点P(X，Y，Z)。普通钢筋的空间曲线方程也可以按照上述方法建立。

2 梁体表面曲面方程

一般而言，箱梁表面由一系列柱面组成，以箱梁梁底曲面为例，准线是圆弧或者抛物线，母线是平行于Y轴的直线。梁体空间模型可以利用放样等操作生成，空间模型生成之后，各个表面的方程也随之生成。大部分情况下，箱梁的表面均可以表示成为由以平行于Y轴的直线为母线和准线构成的柱面。其方程表达如下

f(x,z)=0

y=0(5)

3 空间干涉判断算法原理

图4 预应力钢束空间干涉

判断钢束之间(或钢束与普通钢筋之间)是否干涉，抽象为数学模型就是计算曲线之间的最小距离，判断该最小距离是否大于2倍的管径(图4)；同样的，钢束与梁体表面的距离可以转换为求解曲线到曲面的最小距离。而最小距离可以通过最优解算法解决，通过建立预应力钢束空间参数方程，达到了将曲线方程消元的目的，从而使得三维最优解问题转换为二维最优解问题，进一步使问题得到了简化。

以钢束之间的最小距离为例，即求解

f(x1,x2)=[(x1-x2)2+(y1(x1)-

y2(x2))2+(z1(x1)-z2(x2))2]1/2

由于钢束空间方程采用分段函数表达，故上述最优解问题难以求出理论解，只能采用数值分析方法解决。本文采用改进的Downhill Simplex Method， Nelder-Mead Simplex(下山单纯形法，简称单纯形法)求解此二元函数极值问题。单纯形法的基本思想是构建n维空间(n是参数个数)，在这个空间中初始化一个n+1边形(通常为等边形)，通过对此多边形进行相关操作，使多边形的最佳顶点的评价函数值最终达到用户的要求，从而使问题得到解决。标准的下山单纯形法，每一步变换的尺度是固定的，而在本文中，首次引入了遗传算法思想，即通过罚函数来控制变换的尺度，使计算能够更加快速地收敛。

对于二元函数，单纯形即为三角形。首先，比较函数在三角形各顶点处的值，最大值的顶点为最差顶点，值最小的顶点为最佳顶点，另一个顶点为次最佳顶点，同时记录三点之间距离与函数值，定义一个基本罚函数；随后通过一系列变化(反射、开拓、收缩)在函数值递减的方向产生新的顶点，用以代替最差顶点，形成新的三角形，在这个过程中，每一步都将生成一个新的罚函数，来决定下一步变形(反射、开拓和外延)的尺度，然后重复这一过程。这一过程将生成一系列可能具有不同形状的三角形，顶点处的函数值越来越小，随着三角形的减小函数值趋于极小值，极值点的坐标随之确定。可以看出，单纯形法的搜索过程是模式化的，其优点是紧凑有效，收敛速度快，程序设计简单。

4 结果及性能分析

基于该方法编制的子程序集成在“混凝土箱梁辅助设计系统” 中[4]。以杭长客运专线(50+80+50)m标准连续箱梁为例，在布置纵向预应力钢束的时候，当用户指定钢束横向分布之后，程序将调用该模块进行空间干涉检算，如果发现存在干涉情况，将提示用户进行修改,如图5所示。

注：8号、9号为程序内部编号，对应钢束名称为T9、T11

该模块在武广高速铁路、郑武客运专线、杭长客运专线等项目的连续箱梁设计过程中广泛运用，使用过程中程序能够快速判断预应力钢束的干涉情况，有效地提高了设计效率与质量。如果在干涉计算之前，加上三维实体空间包围盒的叠加判断，效率将会得到进一步提升。表1为算法性能的部分统计数据。

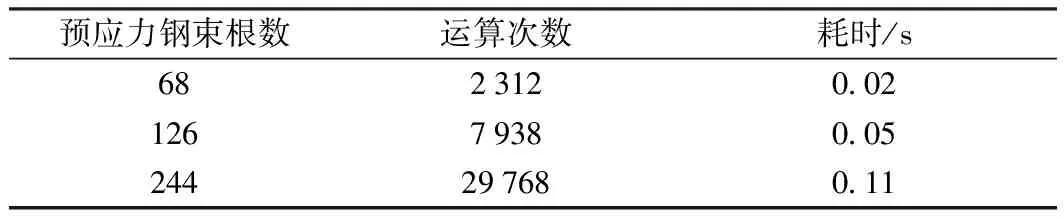
表1 算法在不同情况下的时间复杂度

5 结语

三维设计是铁路桥梁设计的趋势所在，将铁路桥梁设计从二维平面拓展至三维空间之后，在带来技术进步的同时，也引发一些依靠常规手段难以解决的问题。例如本文中提到的预应力钢束空间干涉等问题，这些问题往往要依靠跨学科的技术手段及强大的数学分析工具来解决，这也是工程设计专业软件开发的一项关键支撑性技术。

[1] 雷慧锋.铁路预应力混凝土梁设计[J].铁道标准设计，1999(8):2-4.

[2] 席光勇.锚索预应力损失的分析与探讨[J].铁道标准设计，2006(7):32-34.

[3] 赵绪满，张世辉，帅一丁.预应力损失对大跨度混凝土连续梁挠度的影响研究[J].铁道标准设计，2011(S1):80-82.

[4] 耿杰.铁路箱梁三维钢筋图绘制系统的研制[J].中国水运，2010(12):226-227.

[5] Wang J， S.A. Chou， C.C. Chen and C.S. Wang， “A Virtual Reality Framework for RC Building Design and Construction Cooperation，” to be presented at the First International Conference on Cooperative Design， Visualization and Engineering， CDVE2004， September 19-22.

[6] 姚玲森.桥梁工程[M].北京:人民交通出版社，1985.

[7] 王福建，吴国雄.道路工程三维建模技术[M].北京:人民交通出版社，2004.

[8] TB100023—2005 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S].北京：中国铁道出版社，2005.