三相电压型逆变器的精确线性化控制

董锋斌 钟彦儒

（1. 陕西理工学院电气工程学院 汉中 723003 2. 西安理工大学自动化与信息工程学院 西安 710048）

1 引言

三相电压型逆变器是一种广泛应用于交流调速、不间断电源、感应加热电源、太阳能及风能发电等领域的功率变换器。随着各种电源应用的普及，人们对三相电压型逆变器系统的性能（稳定性、动态品质和鲁棒性）要求越来越高。在逆变器电路拓扑一定的条件下，优越的控制策略是提高逆变器性能的一个关键因素，因而控制策略的研究对逆变器的高效应用具有十分重要的意义[1,2]。

三相电压型逆变器系统主拓扑及其组成元器件决定了其电路本质为时变的、耦合的及多输入多输出的非线性系统。为了满足这个非线性系统的动态响应和控制精度的要求，这就需要用非线性控制理论和技术对其进行分析。基于微分几何理论的精确线性化是非线性控制理论中的一种基本设计方法，它为非线性系统提供了线性化控制和解耦控制的工具，已广泛应用于电力系统、航空航天等领域中[3,4]。对于电力电子变换器这类典型的开关非线性系统，如果能建立其仿射非线性系统数学模型，也可以应用精确线性化控制来提高系统的控制效果。经文献检索，它已被成功地应用到Buck变换器[5,6]、 Boost变换器[7]、三相PWM整流器[8,9]和单相全桥逆变器[10]等中。关于此方法应用到通用的三相电压型逆变器的控制研究却未见文献报道。

受文献[10]的思路启发，本文将精确线性化方法应用于三相电压型逆变器系统中。首先建立了系统仿射非线性数学模型，再从理论上表明了系统模型满足状态反馈精确线性化的能控性条件和对合条件，推导出非线性状态反馈控制律。对非线性坐标变换后得到的线性系统，利用二次型最优控制策略得到状态反馈控制律。最后通过仿真和实验表明所采用的控制方案的合理性。

2 三相电压型逆变器的仿射非线性模型分析

一般的三相电压型 PWM逆变器的电路拓扑及各个变量的参考方向如图1所示。图中Lf、Cf为滤波电感和电容，R为负载电阻。Skj为开关，其中k∈{a,b,c}，j∈{p,n}。假设开关为理想开关，忽略其死区时间，忽略滤波电感、电容的内阻。由于任一瞬时每相每桥臂中只有一个开关器件导通，定义一个开关函数 Sk，k∈{a,b,c}，当 Sk=1，表示与p相连；Sk=0，表示与n相连。

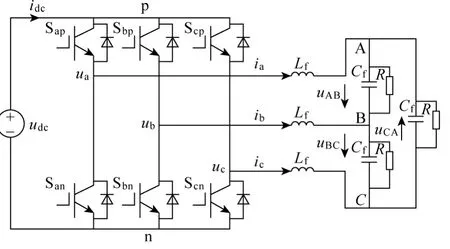
图1 三相电压型逆变器电路拓扑Fig.1 Circuit diagram of three-phase voltage source inverter

定义虚拟线电流iab=ia–ib，ibc=ib–ic，ica=ic–ia；线开关函数sab=sa–sb，sbc=sb–sc，sca=sc–sa。依据六个开关的八种状态和基尔霍夫定律可以得到[11]

式（1）表明三相电压型逆变器模型是一个多输入、多输出及强耦合的非线性系统。由于iab=ia–ib，ibc=ib–ic，uAB+uBC+uCA=0，iab+ibc+ica=0。式（1）中第三行可由第一行、第二行联立推导出，第六行可由第四行、第五行联立推导出。故式（1）中的第三行、第六行可略去。式（1）中存在开关函数，引入开关周期平均算子式（2）将其变换为连续的系统，其中Ts为开关周期，x(t)为电路中的某电量。

对式（1）求开关周期平均后，得到式（3），式中各量均为开关周期平均值，为讨论方便，各变量仍保持原有书写格式。其中的dab=da–db，dbc=db–dc，dca=dc–da，它们均为线间占空比。逆变器系统的主要输出是线电压，控制输入是占空比。

式（3）表明三相电压型逆变器模型经化简后是一个2输入、2输出的非线性系统。

选取状态变量、输入变量分别为x、u。其中

3 三相电压型逆变器的精确线性化

3.1 2输入2输出系统精确线性化条件的验证

精确线性化条件（1）满足后再验证D1～D4这4个相量场的集合是否在x=x。处每个相量场都是对合的。

由式（4）和式（6）知，g1、g2、adfg1、adfg2均与x无关，为恒相量场，任意两个恒相量场的李括号为零相量，零相量表示为相量场的平凡线性组合，因此D1～D4均是对合的，精确线性条件（2）满足。

在验证精确线性化条件时，4个相量场组成的矩阵和4个相量场均与x无关，说明此非线性系统可以在全局范围内线性化，实现解耦控制。即对所给定的三相逆变器至少存在着一组输出函数，使得系统的相对阶有定义且总阶数r等于系统的维数n，以便实现状态反馈线性化。

在确定满足精确反馈线性化条件后，定义了相量相对阶，下面通过李导数计算确定在给定输出函数的情况下系统的相对阶。

对输出h1(x)=x3–uABref，有

由式（7）可知，对输出h1(x)的关系度r1=2。对输出h2(x)=x3–uBCref，有

由式（8）可知，对输出h2(x)的关系度r2=2。可以验证2×2维矩阵

式（9）为非奇异矩阵。所以系统的总阶数为4，因此可直接通过坐标变换将系统转化成一个完全能控的线性系统。若系统的总阶数不等于 4，必须另找输出变量函数。

3.2 求解坐标变换和非线性状态反馈控制律

在状态变化范围内，系统可化为第一类标准型，通过以下坐标变换：

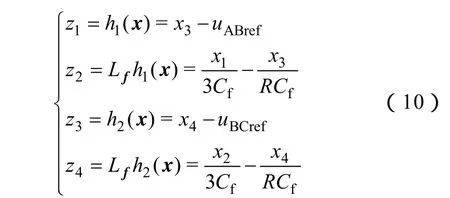
由式（10）可得

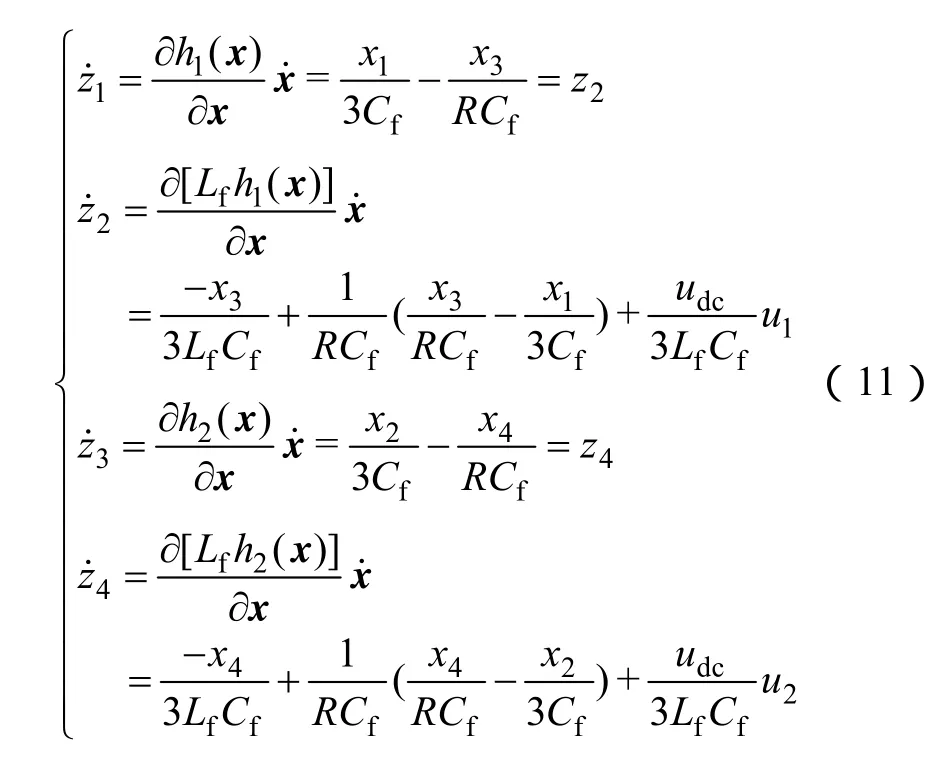
4 二次型最优控制中反馈增益矩阵选择

对于式（12）的线性系统，根据最优控制原理，二次型性能指标为

式中，Q为正定或半正定对称矩阵；R为正定对称矩阵。

要使性能指标函数为最小，则最优控制为

反馈增益矩阵

式中，P为黎卡提代数方程PA+ATP–PBR-1BTP+Q=0的正定对称解。

在黎卡提代数方程中，A、B为已知矩阵，选取不同的R、Q矩阵，则P矩阵不同，反馈增益矩阵K也不同，对应系统特征方程的特征根不同，系统的动态响应也不同。

系统闭环控制的主要目标之一是系统受到干扰后，使系统的状态变量尽快收敛到期望值。根据三相电压型逆变器的工作原理，构造二次型性能指标积分变量第一项为

图2 三相电压型逆变器控制图Fig.2 Control diagram of three-phase voltage source inverter

5 仿真和实验验证

5.1 系统参数

为验证控制策略的合理性，对系统进行仿真和实验研究。参数如下：直流电压udc=150V，给定输出电压峰值为 100V，输出频率为 50Hz，开关周期为Ts=0.1ms，三相对称负载电阻R=20Ω，输出滤波电感Lf=5mH，电容Cf=5μF。

将上述参数带入式（19）和式（20）中，利用Matlab指令K=lqr(A,B,Q ,R)，可求出反馈增益矩阵

参数R在控制过程中，通过输出电压和流过电阻的电流进行参数辨识。仿真采用 PSIM软件，实验采用TMS320F2812 DSP为控制器，功率器件选用SKM 50 GB 121D。

5.2 系统仿真和实验波形

5.2.1 系统启动实验波形

图3为输出电压和电感电流仿真启动波形，从仿真波形看启动速度快，过渡过程时间不到半个输出周期；图4为输出电压和电感电流实验启动响应波形，过渡过程时间为半个输出周期左右，输出电压基本无超调。系统稳态后，输出电压幅值无静差，频率无静差。

图3 输出电压与电感电流启动响应仿真波形Fig.3 Start-up simulating behavior of output voltage and inductive current

图4 输出电压与电感电流启动响应实验波形Fig.4 Start-up experimental behavior of output voltage and inductive current

5.2.2 负载扰动实验波形

负载变化为20Ω→10Ω→20Ω，系统的仿真响应波形如图5所示，实验波形如图6所示。从输出电压和电感电流波形可以看出，系统在负载突变后输出电压幅值有很小的波动，但很快恢复稳定，完全跟随给定且无静差，电感电流也在很短时间内到达新的稳态，说明系统抗负载扰动能力强。

图5 负载突变时仿真波形Fig.5 Dynamic simulating response of load variation

图6 负载突变时实验波形Fig.6 Experimental dynamic response of load variation

5.2.3 直流电压扰动实验波形

直 流 电 压 变 化 为 150V→180V→150V 和150V→120V→150V，系统的仿真波形如图7所示，实验波形如图8所示。从输出电压和电感电流波形可以看出：直流电压变化时，输出电压和电感电流基本恒定，说明对直流电压变化扰动抵抗能力很强。从式（13）可知，控制占空比对直流电压波动有前馈作用。

图7 直流电压突变时仿真波形Fig.7 Dynamic simulating response of DC voltage variation

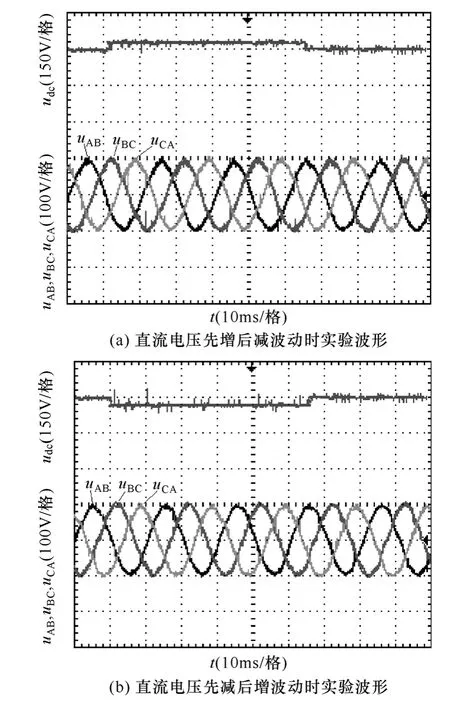
图8 直流电压突变时实验波形Fig.8 Experimental dynamic response of DC voltage variation

6 结论

本文将精确线性化和最优控制方法应用到三相电压型逆变器这个多输入、多输出及强耦合的非线性系统中去。从理论上证明了建立的仿射非线性模型满足精确线性化的条件，推导出状态反馈控制规律。为验证控制策略的合理性，对系统进行仿真和实验研究。仿真和实验结果表明，采用该控制策略系统具有良好的动态响应能力和较强的鲁棒性。

[1] 郑雪生, 李春文, 汤洪海, 等. 三相 PWM 电压型逆变器的积分滑模控制[J] . 电工技术学报, 2007,22(12): 105-109.Zheng Xuesheng, Li Chunwen, Tang Honghai, et al .Integral sliding mode control for three-phase PWM voltage source inverter [J]. Transactions of China Electrotechnical Society, 2007, 22(12): 105-109 .

[2] 戴珂, 王舰威, 陈睿, 等. 两种典型的三相 SPWM逆变器电路比较[J] . 电工技术学报, 2012, 27(2):82-108.Dai Ke, Wang Jianwei, Chen Rui, et al . Comparison research on two typical three-phase SPWM inverters[J]. Transactions of China Electrotechnical Society,2012, 27(2): 82-108.

[3] 张波. 电力电子学亟待解决的若干基础问题探讨[J] . 电工技术学报, 2006, 21(3): 24-35.Zhang Bo. Discussion on several fundamental problems necessary to be solved in power electronics[J]. Transactions of China Electrotechnical Society,2006, 21(3): 24-35.

[4] 胡跃明. 非线性控制系统理论与应用[M]. 北京: 国防工业出版社, 2005.

[5] 邓卫华, 张波, 胡宗波, 等. CCM Buck变换器的状态反馈精确线性化的非线性解耦控制研究[J]. 中国电机工程学报, 2004, 24(5): 120-125.Deng Weihua, Zhang Bo, Hu Zongtm, et a1. Research of nonlinear decoupled control law using state variable feedback linearization method based on the CCM Buck converter[J]. Proceedings of the CSEE,2004, 24(5): 120-125.

[6] 帅定新, 谢运祥, 王晓刚. 基于状态反馈精确线性化Buck变换器的最优控制 [J]. 中国电机工程学报,2008, 28(33): 1-5.Shuai Dingxin, Xie Yunxiang, Wang Xiaogang.Optimal control of Buck converter by state feedback linearization[J]. Proceedings of the CSEE, 2008,28(33): 1-5.

[7] 邓卫华, 张波, 丘东元, 等. CCM Boost变换器状态反馈精确线性化与非线性PID控制研究[J]. 中国电机工程学报, 2004, 24(8): 45-50.Deng Weihua, Zhang Bo, Qiu Dongyuan, et a1. The research of state vailable feedback linearization method on the CCM Boost converter and nonlinear PID control law [J]. Proceedings of the CSEE, 2004,24(8): 45-50.

[8] 邓卫华, 张波. 丘东元, 等. 三相电压型PWM整流器状态反馈精确线性化解耦控制研究[J]. 中国电机工程学报, 2005, 25(7): 97-103.Deng Weihua, Zhang Bo, Qiu Dongyuan, et al.Research of decoupled control law using state variable feedback linearization method of three phase voltage source PWM rectifier[J]. Proceedings of the CSEE, 2005, 25（7): 97-103.

[9] 朱晓荣, 彭咏龙, 李和明, 等. 电流型PWM整流器的非线性控制[J]. 中国电机工程学报, 2007, 27(28):96-101.Zhu Xiaorong, Peng Yonglong, Li Heming, et al.Nonlinear control of current-source PWM rectifier[J].Proceedings of the CSEE, 2007, 27（28): 96-101.

[10] 帅定新, 谢运祥, 杨金明, 等. 基于状态反馈精确线性化单相全桥逆变器的最优控制[J] . 电工技术学报, 2009, 24(11): 120-126.Shuai Dingxin, Xie Yunxiang, Yang Jinming, et al.Optimal control of single-phase full-Bridge inverters by state feedback linearizationrans[J]. Transactions of China Electrotechnical Society, 2009, 24(11):120-126 .

[11] 徐德鸿. 电力电子系统建模与控制[M]. 北京: 机械工业出版社, 2006.

[12] 刘小河. 非线性系统分析与控制引论[M]. 北京: 清华大学出版社, 2008.