基于双向MIMO中继系统的一种预编码策略

张延武，居美艳

（河海大学 江苏 南京 211100）

中继通信技术近年来研究广泛，利用中继节点实现通信接力的方式可以显著提高无线通信系统的性能[1]。当中继节点装备多根天线时，便形成了MIMO中继系统。对于单向MIMO中继系统的性能提升，理论研究已经成熟，常见方法是联合源节点预编码矩阵和中继节点转发矩阵进行最优化求解[2]。由于更加符合实时性要求，双向MIMO中继系统成为了目前研究热点[3-5]。

目前很多文献对双向MIMO中继系统采取的性能研究，是基于双时段的模型[3-5]。即时段1信号被发送到中继，时段2由中继进行信号转发。在时段2中，中继节点要面对两个信道进行预均衡，计算复杂度较高。文献 [3]考虑了MMSE（Minimum Mean Square Error，最小均方误差）准则下的最优预编码矩阵，但是在中继矩阵简略了对目的节点本身信号的处理，会有性能上的损失。文献[4]和[5]假设模型并求出最优解，但是都是建立在中继节点瞬时高效率的假设上，难以实际应用。在文中提出的模型中，中继节点分时段对通信节点进行信号转发，各阶段预编码矩阵遵循MMSE准则，以达到信号的可靠传输。

文章推导了该模型下的算法及其复杂度，仿真了该系统的误比特率，对于双向MIMO中继系统的可靠性传输的研究具有参考意义。

1 系统模型

如图1所示，考虑由两个对等通信节点（1，2），一个中继节点（R）构成的MIMO通信系统。节点1，2分别装有N根天线，中继节点R装备M根天线。通信过程分为3个时段。在时段1，节点S1、S2同时发送信息，节点i发出的信号矢量，i=1，2，其中为通信节点i发出的 N×1信号矢量，而Bi为节点i处的N×N预处理矩阵。此时，中继节点的接收信号yr有

式中，Hr，1，i=1，2 是中继节点到通信节点 i的 M×N 矩阵，是中继节点处的M×1噪声矢量。

图1 系统结构图Fig.1 Structure of the system

时段2中，中继节点用M×M转发矩阵F1对合并接收信号yr处理后，向节点1发送信号，时段3中，中继节点向节点2发送用M×M转发矩阵F2处理yr后的信号。根据式（1），节点1和2处的接收信号为

式中 Hi，r，i=1，2 是通信节点 i到中继节点的信道矩阵，ni，i=1，2是节点i处的噪声矢量。

由于节点i已知自身的发送信号si和信道状态信息Hi，rFHr，iBi，则（2）、（3）式所表示的接收信号中的自身信号部分可以消除，据此，通信节点处有用接收信号可以表示成下式：

2 三时段双向MIMO中继系统性能分析

为了分析三时段双向MIMO中继模型的系统性能，文章介绍所提模型各时段预编码处理方法，完成从发送到接收完毕的一个工作流程的理想信号分析。然后分析系统误码率，介绍与传统方法的不同所在。最后分析算法的复杂度，给出本文算法与经典方法的乘法复杂度对比。

2.1 工作流程

时段1：

通信节点对发送信号的预均衡矩阵Bi遵循MMSE准则：

其中HH为矩阵H的转置矩阵，参数βi，r为通信节点i到中继节点预编码矩阵中的缩放因子，作用是为了保证发射信号的功率恒定。

根据文献[1]，缩放因子 βi，r为

中继节点R在接收到合并信号yr后，对yr乘以两路功放因子 β-11，rβ-12，r，以消除其中一项因子，另一项将在目的节点进行消除。

根据式（1），有

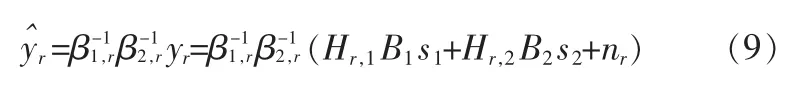
时段2:

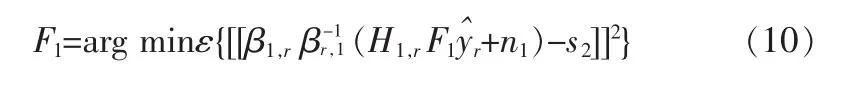
式中为预均衡矩阵，对（10）式求解

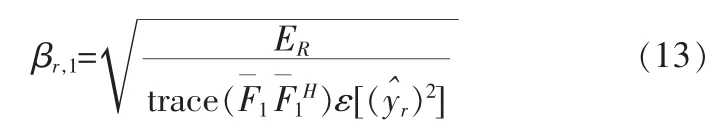
式中ER为中继节点R的功率，为中继节点向通信节点 1 的转发矩阵，βr，1为功控因子为信号的功率

时段2结束后，进入时段3，中继节点向通信节点2发送信号，工作流程与时段2具有对称性，分析时段2结束后所得信号s2的误码率采用蒙特卡罗方法时，统计的误码性能即为整个系统的误比特率。

此时，系统完成一个通信流程。由于在时段2，3采用对通信节点分步发送的方式，避免了文献[3]中因对通信节点同步发送，造成的中继处理矩阵F不对称的问题。文献[3]所代表的2时段双向MIMO中继模型中，对合并接收信号yr处理后的信号要经过不同信道到达各通信节点，要把对中继与通信节点间的各条信道的预处理集中在中继处理矩阵F中。具体的处理就是按中继天线数与通信节点天线数的不同比例情况下分类讨论最优解[6-7]，中继处理矩阵F过于复杂，造成时段2的发送环节瞬时计算量过大。下面推导提供了文中继处理矩阵Fi与[3]的中继处理矩阵的计算量对比，表明了文章中模型简化了通信流程的计算复杂度。

2.2 算法分析

利用了点到点分步执行MMSE准则下的预编码，避免了联合优化方案中矩阵反复迭代导致计算量过大的问题。节点1，2天线数为N，中继节点天线数为M。

文章所提算法的乘法复杂度为

文献[3]所提算法的乘法复杂度涉及矩阵的奇异值分解，文献[8]给出的一种较先进的计算机奇异值分解的方法，指出其数量级约为20n3，我们这里的统计就按照这个简化值计算。

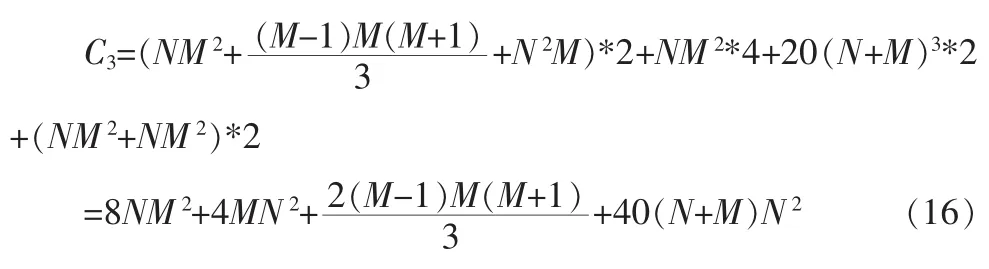
由表1可以看出，当简化奇异值分解计算时，文献[3]给出算法的复杂度约为本文算法的10倍，文中所提算法拥有较低的复杂度。

表1 不同天线数下的乘法复杂度比较（N=M=4）Tab.1 Multiplication complexity of different antenna number

3 仿真结果与分析

采用Matlab软件对所提供算法性能进行仿真，假定每对天线间信道相应服从具有零均值的复高斯独立同分布，并假设所有节点可以通过反馈信道获得实时的信道状态信息。实验：中继节点天线数Nr=4，通信节点天线数Ni=4，i=1，2。为了考察不同算法的预编码性能，统一在时段1进行简单的MMSE准则下的预编码，以误比特率（BER）性能作为系统性能衡量指标，比较了本文策略，传统ZF准则下两条极联策略和经典的两时段双向MIMO策略的系统性能。由于系统模型有细微差别，这里的误码率都是统计从节点1到节点2的误比特率，并非同时统计两个通信节点。

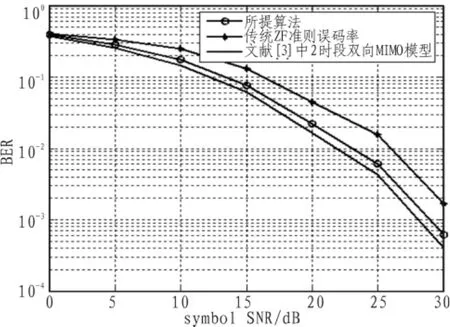
图2 算法误码率比较Fig.2 Comparison of algorithms on BER

图2给出了各预编码策略间误比特率的比较，横坐标为信噪比（SNR），纵坐标为误比特率（BER）。从图中可以看出，所提算法与传统算法相比，误比特率性能接近，且优于传统ZF准则下的策略。

4 结 论

文中提出了一种具有低计算复杂度的3时段双向MIMO中继模型和相应的预编码算法，所提方案误码性能接近传统的2时段双向MIMO模型，简化了中继预处理矩阵。在复杂了系统工作流程的同时，取得了较低的计算复杂度。仿真结果证明了本文算法牺牲较少的性能后较大地降低了传统方法的计算复杂度。

[1]Go′mez-Vilardebo′J，Pe′rez-Neira A I，Na′jar M.Energy efficient communications over the AWGN relay channel[J].IEEE Trans.Wireless Commun，2010（9）:32-37.

[2]Rong Y，Tang X，Hua Y.A unified framework for optimizing linearnon-regenerativemulticarrierMIMOrelaycommunication systems[J].IEEE Trans.Signal Process，2009（57）:4837-4851.

[3] Rong Y.Two-way amplify-and-forward MIMO relay communications using linear MMSE receiver[J].IEEE Trans.Communications Theory Workshop，2011（3）:55-59.

[4]YUE Rong.Joint source and relay optimization for two-way linearnon-regenerative MIMO relay communications[J].IEEE Trans.Signal Processing，2012，60（12）:6533-6546.

[5]XU Sheng-yang，HUA Ying-bo.Optimal design of spatial source-and-relay matrices for a non-regenerative two-way MIMO relay system[J].IEEE Trans.Wireless Communications，2011，10（5）:1645-1655.

[6]Rong Y.Optimal joint source and relay beamforming for MIMO relayswith direct link[J].IEEE Communication Letters，2010，14（5）:390-392.

[7]Yu Y，Hua Y.Power allocation for a MIMO relay system with multiple-antenna users[J].IEEE Trans.Signal Process，2010，58（5）:2823-2835.

[8]Jesse L.Barlow.More accurate bidiagonal reduction for computing the singular value decomposition[J].SIAM Journal on Matrix Analysis and Applications，2002，23（3）:761-798.