Σ-Δ模数转换器工作原理及简单分析

张乐乐 ， 张子阳 ， 张启升

（1.中国地质大学（北京）地球物理与信息技术学院，北京 100083；2.地下信息探测技术与仪器教育部重点实验室 北京100083）

A/D转换器是一种用来将连续的模拟信号转换成适于数字处理的二进制数的器件，传统的A/D转换器有双积分式、逐位比较式以及并行直接比较式等。但是在人类的科学技术发展中，传统的A/D转换器精度已经无法满足人们的需求，数据转换精度的提高已经成了必然的要求。目前16位以上的高分辨率的A/D转换器被人们大量的使用，但是采用传统的双积分式或者其他的A/D转换器无法实现高精度的目标，为了提升采集精度，人们采用了∑-ΔA/D转换器，在∑-ΔA/D转换器中，转换器的模拟部分对电路的占用较小，而且电路比较稳定，所以被越来越广泛地应用于很多仪器中[1]。在∑-ΔA/D转换器中最核心的部分是∑-Δ调制器，它采用了远高于奈奎斯特采样频率的采样技术，即过采样技术，使量化噪声在频带内重新分配，从而使量化噪声在更宽的频带内分布，这样可以降低量化噪声获得更好的采集信号，同时，1位的量化器和噪声成形技术也应用于∑-Δ调制器，进一步强化了∑-Δ调制器的优势，可以更方便地和数字电路集成，实现真正意义上的系统集成。本文主要介绍采用过采样技术的∑-ΔA/D转换器。

1 ∑-ΔA/D转换器的原理概述

∑-ΔA/D转换器的工作原理，就是将初次转换后的数字信号再做信号除噪处理。模拟量进入转换器，要先在∑-Δ调制器中做一次求积，同时将输入的模拟量转换为数字信号，在求积以及转换成数字信号的同时，信号会夹带一定的量化噪声，使结果产生失真。采用将转换后的数字量以低频率一位一位的进行输出，同时使输出的数字量经过一个低通滤波器，将量化噪声过滤掉后再降频就可以得到比较精确的输出结果了。总体来说，∑-ΔA/D转换器有两大部分，模拟部分和数字部分，模拟部分是一个∑-Δ调制器，主要使采用过采样技术采样后信号经过调制器，使量化噪声分布更广，并且输出一位一位的数据位流，数字部分是一个数字滤波器，它对模拟部分输出的数字量进行除噪处理，滤除大部分的量化噪声，并对调制器的输出降频至奈奎斯特频率和进行进一步的量化，最终得到输出结果。图1为∑-ΔA/D转换器的原理图。

图1 ∑-ΔA/D转换器的原理图Fig.1 diagram of the Σ-ΔA/D converter

2 Σ-Δ调制器的原理

2.1 过采样技术

过采样是使用远大于奈奎斯特采样频率的频率对输入信号进行采样[2]。设系统原来的采样频率为fa，现在以远大于原来采样频率的频率即以N×fa的频率进行采样，其中N＞1，此时开始分布在0～fa/2频带内的量化噪声分布到0～N×fa的频带内，即量化噪声的频谱分布发生了变化，当N＞＞1时，量化噪声在系统的频带之内的量化噪声就会减少，这就是过采样技术。补充一下系统的信噪比。信噪比即信号功率与噪声功率的比值，设信号的功率为，已知噪声e（kT）的功率为为转换器的字节长，则信号功率与噪声功率之比为

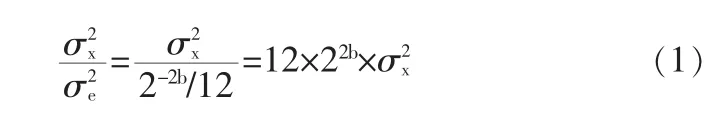
表示成分贝数，则为

2.2 噪声整形原理

量化噪声是影响转换器精度的最主要的原因，如上述所说仅采用过采样技术还不能满足∑－ΔA/D转换器对结果精确度的要求，为了降低量化噪声对结果的影响，所以人们又采用了噪声整型原理，利用反馈克服过高取样所造成的技术困难并且使量化噪声在低频频带内分布的更少。再者，由于数字滤波器在工作过程中由于移位等也会生成一部分噪声，噪声整形就可以很好地解决这一问题，噪声整形处理再量化噪声，低频频带内的噪声将会大大减少，大部分的量化噪声就被推向更高的频段，这样在∑－Δ调制器后加入低通滤波器，就可以有效地滤除信号带宽外的量化噪声，大大提高了系统性能。与前面的简单过采样相比，总的噪声功率虽未改变，但噪声的分布发生了变化。在∑－Δ调制器中采用更多的积分与求和环节，可以提供更高阶数的量化噪声成形[4]。

2.3 一阶噪声成型原理

图2为一阶∑－Δ调制器的结构原理图，分析此结构可以得到以下方程：

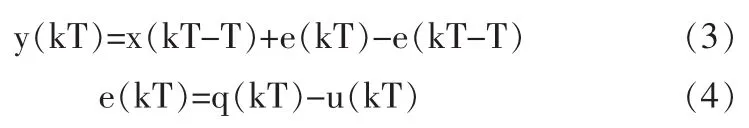
图2 一阶∑－Δ调制器的结构原理图Fig.2 Structural of one-order sigma-delta modulator

对式（3）（4）进行Z变换得到一阶调制器的传输函数为：

这表示一阶调制器的输入信号的一个采样时钟延迟和量化误差的一阶差分。

2.4 二阶噪声成型原理

图3显示二阶∑－Δ调制器结构原理。2次噪声整形电路是进行2次低频提升和低频衰减的电路，即在∑－Δ调制方式l bit量化器的前后，分别加2级积分器和微分器构成的，如同1次噪声整形简化方式一样，2次噪声整形使噪声分布斜率更加陡峭，低频区量化噪声得到进一步降低[5]。

根据线性模型可推出二级∑－Δ调制器的方程为

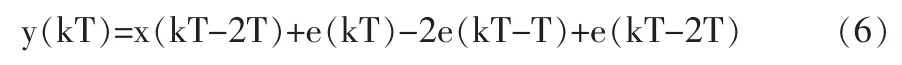
经过Z变换可得

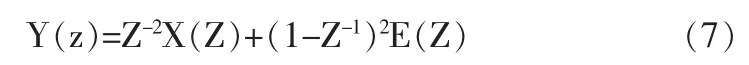
图3 二阶∑－Δ调制器结构原理图Fig.3 Structural of two-order sigma-delta modulator

可以看出由一阶调制器的级联而得到的二阶调制器的输出包括输入信号的2个采样周期延迟和量化误差的2阶差分。

由此可以推理得出L阶调制器的传输函数为：

令 Hk（Z）=Z－L，Fn（Z）=（1－Z－1）L，则信号传输函数为 Hk（Z），是 L个延时（全通函数），噪声传输函数为 Fn（Z），是 L阶整形，即高通函数，将量化噪声推向更高的频域[6]。

图4为信噪比随过采样率和阶数的变化。可以看出采样频率每增加2倍，在L=1时，信噪比提高9 dB，L=2时，信噪比提高15 dB，时，信噪比提高21 dB。过采样率以及阶数越高，∑－Δ调制器的量化信噪比越好。但是过采样率和调制器的阶数不会一直提高，因为现代工艺还未达到这个水平，硬件实现难，而且调制器的阶数过高会造成系统的不稳定，不利于结果的输出[7]。

图4 信噪比随过采样率和阶数的变化Fig.4 Change of SNR with the sampling rates and the orders

3 数字抽取滤波原理

∑-Δ调制器的输出，信号频谱分布在基带内，而量化噪声则分布在基带之外，所以可以利用数字信号低通滤波器来获得想要的输出。而在一般情况下，为了方便以后对输出信号进行处理，则需要将输出信号的频率将至奈奎斯特频率。数字低通滤波器通常分为两类，有限冲击响应滤波器（FIR）和无限冲击响应滤波器（IIR），在降频变换中，通常采用可以获得精确线性相位的FIR数字滤波器[8]。

滤波以后，进行对数据的重采样，它是通过每输出M个数据抽取1/M个数据完成的，这种方法也叫做输出速率降为的采样抽取，即减采样，最终输出频率降至奈奎斯特频率。通常，减采样后的离散序列的频谱将会出现混迭，为了避免混迭，可在信号减采样前用低通滤波器对信号进行滤波，如图5所示，称该低通滤波器为抽取滤波器。一般的，如果低频信号 z（n）的频谱是带限的，即在区间[-π，π]范围内有

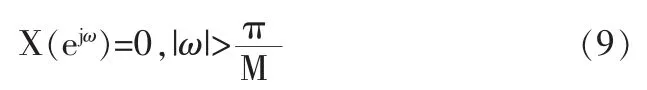
则M倍减采样后信号的频谱不会发生混叠[9]。式称为序列减采样不混叠的奈奎斯特条件，即奈奎斯特频率为π/M（数字频率）。

图5 倍减采样滤波系统Fig.5 M-fold downsampling filter system

若信号 x（n）需保留的最高频率分量为 ωm/M（ωm＜π），即减采样后的信号在频谱范围[0，ωm]内无混叠，在频率范围[ωm，π]允许存在混叠。则抽取滤波器H（z）的幅度响应可为

M倍减采样滤波系统输出信号的时域表达式可写为

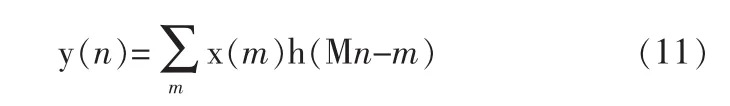
由上式可知在计算M倍减采样滤波系统的输出时，只需计算抽取滤波器每M个输出中的一个样本，所以可以减少系统的计算量[10]。通过抽取滤波器以后，我们就可以得到想要的结果了。

4 结束语

高精度是∑-ΔA/D转换器最突出的优点，其转换精度一般都在16位以上，在相同精度的模数转换器中∑-ΔA/D转换器价格最低，作为测量系统的核心元件，它会提升整个系统的性价比，而且越来越多的应用于数字信号处理系统中。但是这种转换器也是存在着很多制约其发展的因素，最突出的就是，∑-ΔA/D转换器以提高采样时间换取精度，应用于对时间要求比较严格的数字信号处理系统比较困难，因此∑-ΔA/D转换器还有更远的路要走。

[1]SchreierR，TemesG.Understanding delta-sigma data converters[M].NJ:IEEE Press，2005.

[2]Stewart R W.An overview of sigma delta ADCs and DAC devices[C]//IEEE Int Sol Sta Circ Conf， London， UK.1995：204-206

[3]Norworthy S.R.，Schreier R，Temes G.C.Delta-sigma data converters theory，design and simulation [J].New York:IEEE，1997.

[4]Rusu A，Tenhunen H.A third-order sigma-delta modulator for dual-mode receivers[J].IEEE Circand Syst，2003，1（4）:68～71.

[5]Peluso V.Design of Low-voltage Low-power CMOS Deltasigma AD converters[J].Kluwer Academic Publishers，1999.

[6]Candy James C，Temes Gabor C.Oversampling Methods for A/D D/A Conversion.Oversampling Delta-Sigma Converters[C]//New Jersey， IEEE Press，1992：2-3.

[7]Bourdopoulos G，Anastassopoulos V，Deliyannis T，et al.Deltasigma modulators:modeling，design and applications[M].London:Imperial College Press，2003.

[8]Malcovatip，Brigatis.Behavioral modeling of switched-capacitor sigma-delta modulators[J].IEEE Trans Circ and Syst，2003，50（3）:352-364.

[9]陈玉东.数字信号处理[M].北京：地质出版社，2005.

[10]尤裕荣，袁洪滨，王春民，等.PWM高速开关阀动态调节特性仿真研究[J].陕西电力，2012（5）：24-29.YOU Yu-rong，YUAN Hong-bin，WANG Chun-min，et al.Simulation of dynamic regulating characteristics of PWM high-speed on-off valve[J].Shaanxi Electric Power，2012（5）：24-29.