复合材料网格圆柱结构减重优化设计①
辛 星
(中国航天科技集团公司四院四十一所,西安 710025)
0 引言
复合材料网格圆柱结构由蒙皮和纵、环向筋条组成,在导弹发动机头锥壳体、运载火箭、大型商用飞机等航空航天结构上有着广泛的应用前景。此结构采用了先进的高模量、高强度炭纤维材料,并辅助以纵、环向筋条梁结构加强,使其满足载荷承载性能和质量比要求。
本文对固体发动机复合材料网格圆柱结构进行优化设计,在满足结构一定的载荷承载能力和屈曲约束条件下,对结构中蒙皮铺层参数和纵向、环向筋条宽度和数量进行了优化计算[1-4],从而降低了结构质量,提高了发动机质量比。其中,考虑到结构尺寸约束条件,所以文中筋条高度不进行优化。本文通过ANSYS有限元计算软件,完成了复合材料网格圆柱结构分析和优化计算。
1 有限元优化计算模型
复合材料网格圆柱结构有限元模型由壳单元和梁单元组成。结构中,蒙皮为壳单元,纵、环向筋条为梁单元,蒙皮与筋条衔接处采用公共节点连接,较准确地模拟了网格结构的实际情况。其中,网格结构有限元模型中总共24 200节点、7 036个壳单元和2 963个梁单元,图1给出了结构示意图。

图1 复合材料网格圆柱结构模型Fig.1 The model of composite cylindrical grid structure
复合材料网格圆柱结构优化计算的特点是设计变量较复杂,其结构中的蒙皮壳单元和梁单元共有5种类型设计变量,分别是蒙皮铺层次序、纵向筋条数量、纵向筋条宽度、环向筋条数量、环向筋条宽度。
在优化计算过程中,如果直接以所有的设计变量同时进行优化计算,将是盲目且困难的。因为所有变量参与计算,将无法确定那些变量对于结构载荷承载性能的影响是主要的,且耗费大量时间。所以,在结构整体进行优化之前,需对设计变量分别进行优化设计。本文采取下列方法,处理5种类型的设计变量。
复合材料网格圆柱结构的蒙皮为壳单元,其铺层优化设计目标要求是确定纤维铺层的最佳铺设角度,铺设角度设计变量范围为0°~90°。
复合材料网格圆柱结构的纵向、环向筋条宽度的优化设计,是选取一系列的筋条模具宽度,数量的优化设计应为整数。所以,其变量为离散变量。本文对离散变量,采取下列连续化处理方法:
(1)蒙皮结构的铺层设计材料参数变化以材料型号作为连续的设计变量,对材料的各个模量参数分别做出插值曲线;
(2)在优化计算过程中,纵向、环向筋条的宽度和数量作为连续的设计变量参与优化计算;
(3)最后,对优化设计变量结果进行圆整化取值。
2 计算方法
2.1 结构固有频率和屈曲问题的求解
结构固有频率问题及屈曲问题的求解归结为求解式(1)的广义特征值问题[5-6]。

其中,[K]、[M]为结构的刚度阵和质量阵;对于固有频率问题,α为结构固有频率的平方ω2;而对于屈曲载荷问题,α为临界屈曲载荷系数λCR。
本文在有限元优化计算分析中,对于固有振动频率问题,采用的是子空间迭代法,而对于屈曲稳定性问题,是求解前一阶或前几阶特征值问题,采用逆幂迭代法,计算前几阶特征值和屈曲模态。
2.2 优化问题的求解
优化设计是求解在一定约束条件下,使得目标函数取得最小值的设计变量Xi(i=1,2,…,n)最优值问题[7],其优化模型如下:

式中 m为约束条件总数;n为设计变量总数;f(X)为目标函数,表示网格结构质量;gj(X)为约束函数,表示结构刚度或结构固有频率及结构边界约束条件;Xi为设计变量。
优化求解算法一般为序列线性规划[7-9]和序列二次规划,本文采用二次规划算法进行优化求解。
3 优化计算结果
在复合材料网格圆柱结构优化[10-11]计算分析中,为了分析各部分参数对结构重量和承载性能的影响,本文采取了如下3种优化方案进行计算,优化先后顺序为方案1、方案2和方案3,每种优化方案计算结果将直接应用到后续方案中。
方案1:只进行蒙皮结构的优化设计,其中包括从0°铺层到90°铺层优化,选择最佳的纤维铺设角度;
方案2:只进行纵向筋条数量和宽度的优化设计;
方案3:只进行环向筋条数量和宽度的优化设计。
在满足约束条件的情况下,蒙皮结构铺层优化结果为0°/90°铺层减重6.3%,0°/±45°铺层减重4.2%。从蒙皮铺层优化结果来看,0°/90°铺层比 0°/±45°铺层优化的效果明显。所以,在进行纵向、环向筋条数量和宽度优化时,蒙皮结构铺层采用了0°/90°的优化结果方案。图2和图3分别给出了复合材料网格圆柱结构纵向筋条数量和宽度的优化曲线。

图2 纵向筋条数量优化Fig.2 The number optimization of oblique rids

图3 纵向筋条宽度优化Fig.3 The width optimization of oblique rids
在满足结构约束条件的情况下,纵向筋条最优数量为113.6条,最优宽度尺寸为6.16 mm。由于生产工艺的要求,纵向筋条条数必须为整数,且为偶数。其中,筋条宽度输入值在每次迭代计算时,必须为一定的离散值。所以,在优化设计计算迭代过程中,对每次的计算结果进行了圆整化处理。表1和表2给出了每次迭代计算结果。
根据以上计算结果分析,复合材料网格圆柱结构纵向筋条最优数量取值为112条,最优宽度尺寸为6 mm。其中,初始设计宽度为8 mm,数量为90条。
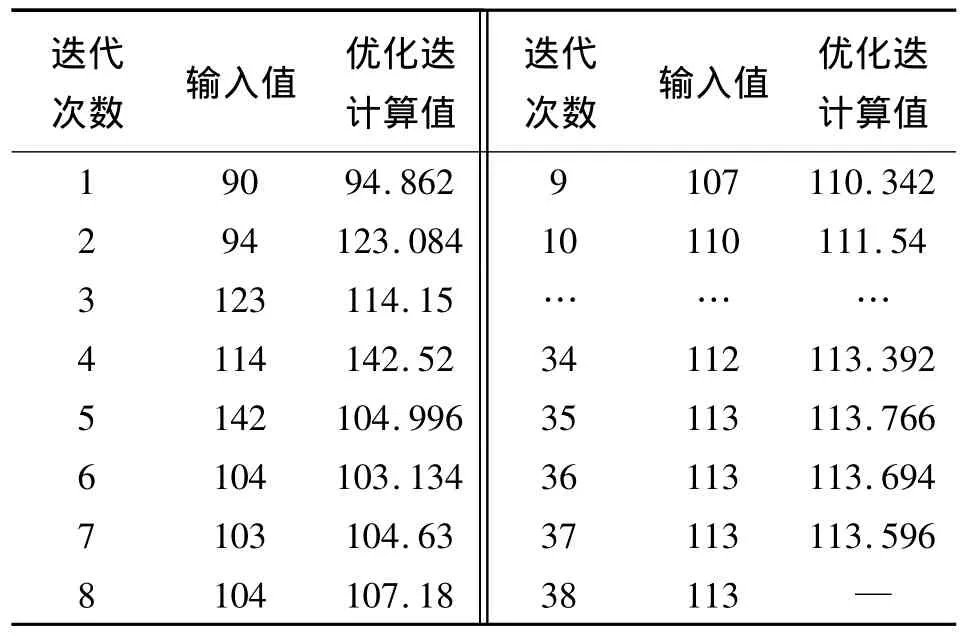
表1 纵向筋条数量优化迭代结果Table 1 The results of oblique rids number in the optimization iteration
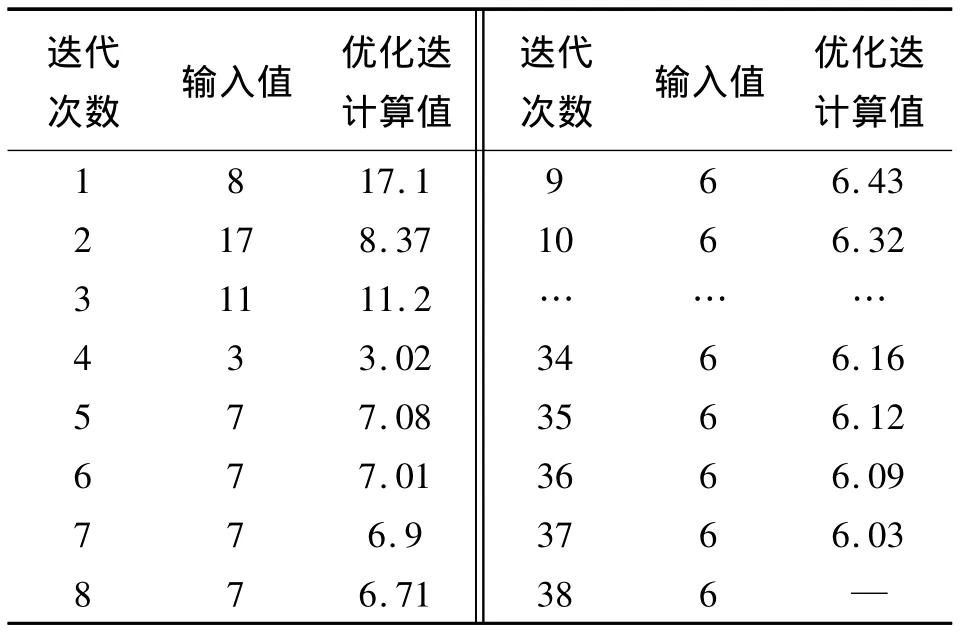
表2 纵向筋条宽度优化迭代结果Table 2 The results of oblique rids width in the optimization iteration mm
图4和图5分别给出了复合材料网格圆柱结构环向筋条数量和宽度的优化曲线。在满足结构约束条件的情况下,环向筋条最优数量为1.02条,最优宽度尺寸为6.4 mm。同样考虑到生产工艺的要求,环向筋条条数及宽度的计算迭代过程进行了圆整化处理,环向筋条数量和宽度每次迭代计算结果类似表1和表2,本文略去了列举。
同理,复合材料网格圆柱结构环向筋条最优设计数量取值为1条,其最优宽度尺寸为6 mm。其中,初始设计宽度为8 mm,数量为3条。
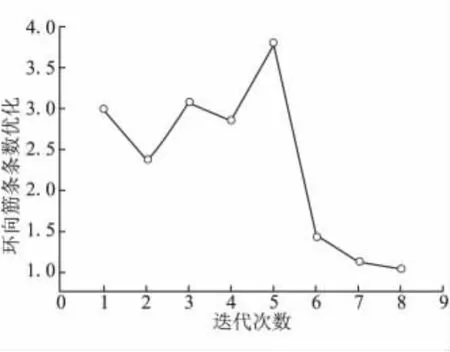
图4 环向筋条数量优化Fig.4 The number optimization of hoop rids

图5 环向筋条宽度优化Fig.5 The width optimization of hoop rids
图6给出了复合材料网格圆柱结构刚度迭代曲线。可知,初始计算结构整体刚度数值为2 010.5,经过迭代优化计算后,结构整体刚度最终收敛于2 003.3,满足其约束条件。

图6 复合材料网格圆柱结构刚度优化Fig.6 The stiffness optimization of composite cylindrical grid structure
表3给出了复合材料网格圆柱结构纵向、环向筋条减重优化设计结果。可知,纵向、环向筋条优化后,结构质量分别减少了5.1%和64.5%;蒙皮结构优化后,质量可减少6.3%(与原结构部位相比),网格整体结构质量共减少21.1%,且所有约束条件和设计变量的要求都能满足。这一优化设计结果,不仅满足结构的载荷承载能力,且提高了发动机结构质量比。
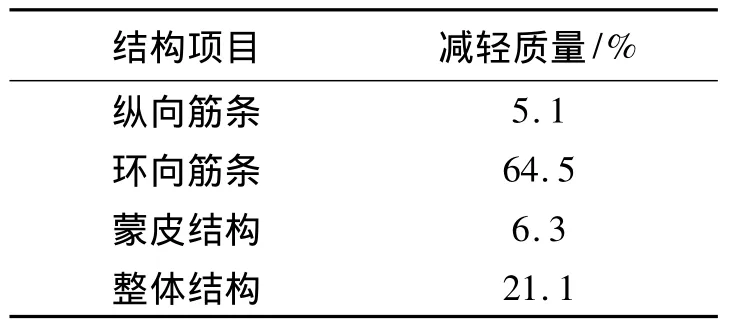
表3 复合材料网格圆柱结构优化结果Table 3 The optimization results of composite cylindrical grid structure
4 结论
(1)对复合材料网格圆柱结构进行了优化设计,在满足载荷约束条件下,给出了结构蒙皮和纵向、环向筋条的优化结果。可知,整体结构质量可减轻21.1%,为提高发动机质量比要求提供了有意义的参考依据。
(2)在优化计算中,针对工程中网格结构筋条工艺生产要求,采用了一种离散设计变量连续化处理方法,并对每一步优化计算结果进行了圆整化处理,满足了结构实际生产工艺要求。
[1] Vasiliev V V,Razin A F.Anisogrid composite lattice structure for spacecraft and aircraft applications[J].Composite Structures,2006,76(1-21):82-189.
[2] Wang J T S,Hsu T M.Discrete analysis of stiffened composite cylindrical shells[R].AIAA 92-2306-CP.
[3] Reddy A D,Valisetty Rao R,Rehfield L W.Continuous filament wound composites concepts for aircraft fuselage structures[J].AIAA Journal of Aircraft,1985,22(3):249-255.
[4] Vidal C A,Kataoka-Filho M,Takahashi W K,et al.Applicati-on of sensitivity for optimization of a satellite structure[R].AIAA 98-1820.
[5] 何景轩.固体火箭发动机复合裙轴压屈曲载荷计算[J].固体火箭技术,1998,21(2):62.
[6] 何景轩,何国强.复合材料格栅结构屈曲特性分析[J].固体火箭技术,2008,31(4):389-392.
[7] 孙焕纯,曲乃泗,林家浩.计算结构动力学[M].北京:高等教育出版社,1990.
[8] 吴徳材,徐元铭,万青.先进复合材料格栅加筋板的总体稳定性分析[J].复合材料学报,2007,24(2):168-173.
[9] 吕恩琳.复合材料力学[M].重庆:重庆大学出版社,1992.
[10] 韩强,黄小清,宁建国.高等板壳理论[M].北京:科学技术出版社,2002.
[11] 杜善义,章继峰.先进复合材料格栅结构(AGS)应用与研究进展[J].航空学报,2007,28(2):419-424.

