某型固体发动机健康状态评估技术研究①

赵汝岩，黄志勇，吴 昊

(1.海军航空工程学院7系，烟台 264001;2.海军航空工程学院 研究生管理大队，烟台 264001)

0 引言

固体发动机作为各种导弹的动力系统，其健康状态好坏将直接影响导弹是否能够正常飞行，并最终命中预定目标。目前，对各类导弹固体发动机的健康状态好坏，采用无损检测的方式判断裂纹、脱粘等缺陷的大小，进而进行判断。而导弹与其他装备的最大区别就是“长期贮存，少量测试，一次使用”。鉴于这种特点，一般情况下只能得到固体发动机每次无损探伤时的健康状态，无法反映出2次探伤之间的时间段内的健康状态及变化趋势。因此，建立基于ER(Evidential Reasoning)算法的测试数据评估模型，引入时间修正，利用ER算法处理评估过程中的不确定性信息，并得到某型固体发动机处于不同健康状态等级的信任度，以定性定量地实现该发动机健康状态的实时评估。

1 健康状态等级

为了更好描述固体发动机的健康状态，从健康管理的角度出发，将固体发动机健康状态分为5个等级［1］，分别为良好、正常、注意、恶化和病态。

(1)良好

良好状态表示固体发动机各项性能指标都在允许范围之内，测试结果为所有测试值均远离阈值，能保证任务的完成，无需进行维护。

(2)正常

正常状态是在平时测试时表现为测试结果在标准值上下一定范围内波动，但不会超出阈值。这种状态基本不影响装备的正常使用，但如果经常出现干扰或恶劣环境，则需要注意，加强监控。

(3)注意

注意状态是指固体发动机无损检测数据接近规定阈值。为保证装备在规定要求的范围内可靠工作，应及时采取维修措施。

(4)恶化

恶化状态是指无损检测数据超阈值现象发生。为保证正常使用，必须及时对出现故障的部件进行维修。

(5)病态

病态状态为无损检测的多个数据超阈值，病态状态是恶化状态的进一步发展。对病态的固体发动机必须进行大修，以保证战备完好率。

2 基于ER算法的测试数据评估模型

2.1 测试数据处理

2.1.1 测试数据的归一量化

测试数据的归一量化为本次测试数据与标准数据的比较值。

首先，计算本次测试数据x与标准数据x0的偏差:

然后，计算归一量化数据λ，计算方法如下:

(1)若标准数据为固定值x0和误差限δ0的形式，则λ按照如下函数计算:

(2)若标准数据为大于或小于一固定值x0的形式，则λ按照如下函数计算:

2.1.2 测试数据的时间修正

利用时间修正对固体发动机无损探伤数据进行实时修正，就可在任一时间对其健康状态作出评估。通常固体发动机的老化失效除瞬间过应力之外，一般都有一个逐渐退化的过程。正常的退化失效故障通常是一个先慢后快的过程。为了准确描述固体发动机健康状态的变化情况，采用如下的时间修正函数［2］:

其中，(T1，T2)为固体发动机缓慢失效时间;(T2，T3)为固体发动机快速老化失效时间。(T1，λ1)、(T2，λ2)的值根据实际退化数据及专家经验确定得到。本文主要在固体发动机缓慢失效时期进行时间修正，根据专家经验，取(T1，λ1)、(T2，λ2)为(2，1)、(12，0.7)。

2.1.3 隶属度的确定

隶属度根据三角模糊数［3］确定，三角模糊数模型根据固体发动机的健康状态实际退化情况及专家经验共同得出，即如下函数:

式中 λ 为归一量化数据;yi(i=1，2，3，4，5)分别表示“良好”、“正常”、“注意”、“恶化”和“病态”的隶属度。

2.1.4 基本可信度的确定

βn，i表示第i个基本属性被评为第n个等级的信任度:

式中 置信度一般取0.9。

2.2 ER算法数学模型

ER算法又称证据推理方法，其数学模型描述如下［4－5］。

2.2.1 基本属性的基本概率指派函数

令mn，i为已分配的概率指派函数，表示第i个测试数据ei支持固体发动机y被评为第n个健康等级Hn的程度;mH，i为未分配的概率指派函数，表示测试数据对固体发动机没有分配给具体健康等级的支持度。mn，i和 mH，i的计算公式:

将 mH，i分解为和，其中

式中 ωi为第i个测试数据的相对权重，且满足0≤ωi为剩余概率量的第 1 部分，表示由于权重而未分配的概率函数;为剩余概率量的第2部分，它是由于评估的不完备性引起的。

2.2.2 广义属性的组合概率指派函数

令mn，I(i)表示所有L个测试数据支持固体发动机y被评为第n个健康等级Hn的程度;mH，I(i)表示测试数据聚合后，固体发动机y没有分配给具体健康等级的程度。

参照2个测试数据的评估聚合表，可给出前i个测试数据的组合概率指派函数:

式中 I(i+1)表示包含i+1个测试数据属性;K为规模化因子，反映了各证据间冲突的程度。

2.2.3 广义属性的组合信任度

2.3 基于ER算法的测试数据评估流程

假设已经获取到某型固体发动机的表征其健康状态的测试数据，则在所建立的基于ER算法的测试数据评估模型的基础上，按照以下流程开展具体的评估工作:

(1)对测试数据按2.1.1节进行归一量化;

(2)利用时间修正函数，对归一量化的测试数据进行修正;

(3)按照2.1.3节确定其在三角模糊函数下的隶属度;

(4)确定基本可信度;

(5)利用ER算法合成计算，确定等级分配信任度。

3 实例分析

3.1 某型固体发动机健康状态测试参数及权重

固体发动机老化失效的主要模式为脱粘、裂纹、软化等［6］。因此，本文选取发动机装药脱粘面积［7］作为某型固体发动机健康状态指标，如表1所示。目前，距上次无损检测时间已有1 a。固体发动机无损探伤数据将直接反映其健康状态，当某一数据超出了规定阈值，则该发动机需要维修处理。因此，任何数据的权重都是相等的，即表1中各个测试数据项目指标权重均为1/3。

表1 固体发动机健康状态指标Table 1 Health status index of solid motor

3.2 健康状态评估评估结果

根据无损探伤测试数据，由式(1)～式(3)可得到固体发动机测试数据归一量化表，见表2。

表2 测试数据归一量化Table 2 Normalization of data

得到未修正的3个指标归一量化向量为(0.771 9，0.820 0，0.770 0)，根据 2.1.2 节中的专家经验，取(T1，λ1)、(T2，λ2)为(2，1)、(12，0.7)。由于目前以及距上次无损探伤已有1 a时间，由式(4)得到时间修正后的测试数据归一量化向量为(0.741 9，0.790 0，0.740 0)，由式(5)～ 式(9)得到这 3 个指标的隶属度如表3所示。取置信度为0.9得到基本可信度分配表，如表4所示。

根据式(11)～ 式(14)，计算基本概率集合 mn，i，结果如下:

表3 指标的隶属度Table 3 Membership of index

表4 基本信任度分配Table 4 Distribute of confidence

根据式(15)计算规模化因子，结果为

根据式(15)进行聚合运算得

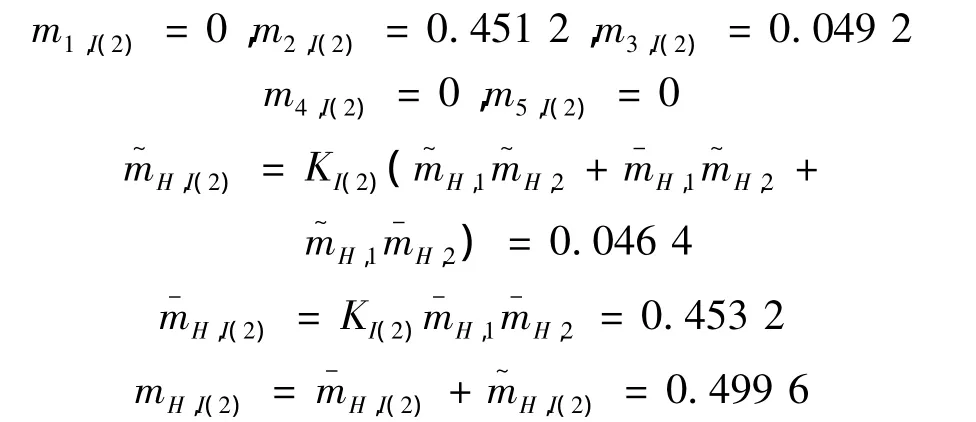
以上给出了2个指标属性的聚合过程，为了得到组合概率，还要与第3个指标属性进行聚合。

由式(16)可得

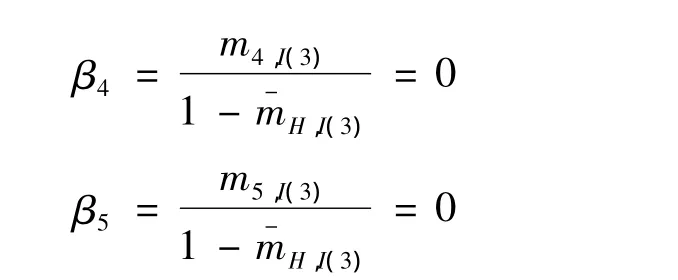
得到合成结果为(0，0.825 7，0.102 2，0，0)。即主发动机健康状态评估结果为“正常”状态的概率为82.57%，评估为“注意”状态的概率为10.22%。

4 结论

(1)建立了基于ER算法的测试数据评估模型，在2次检测之间中引入了时间修正，利用ER算法处理由三角模糊数理论计算的隶属度，得到某型固体发动机处于不同健康状态等级的信任度，实现了该发动机健康状态的实时评估。

(2)从评估结果可看出，该评估模型能处理由不确定信息产生的不确定性，并给出未知信息的信任度，不仅能实现某型固体发动机健康状态等级的定性描述，而且评估结果能定量表示不确定性的具体程度。

(3)基于ER算法的测试数据评估模型，还可扩展到对环境信息、历史信息等其它相关信息进行评估处理，对处理后的结果再次利用ER算法进行多元信息融合评估，更加真实反映该发动机的健康状态。该模型如果用于武器装备健康管理系统，能实现武器装备由修复性维修、预防性维修向预计性维修的转变，推动武器装备管理理念、维修模式、维修体制的创新。

［1］刘建敏.装甲装备机械系统故障预测与健康管理系统的研究［R］.GF-A0129183N.

［2］刘春和，路祖建，等.武器装备可靠性评定方法［M］.北京:中国宇航出版社，2009:10-11.

［3］刘开弟，庞彦军，周少玲.模糊数学存在的问题及解决方法［J］.河北工业大学学报，2011，40(4):106-112.

［4］Yang J B.Rule and utility-based evidential reasoning gapproach for complex decision analysis［J］.European Journal Operational Research，2001，131(1):31-61.

［5］Yang J B，Xu D L.On the evidential reasoning algorithm for multiple attribute decision analysis under uncertainty［J］.IEEE Transactions on Systems，Man，and Cybernetics Part A:Systems and Humans，2002，32(3):289-304.

［6］张炜，张玉祥.导弹动力系统故障机理分析与诊断技术［M］.西安:西北工业大学，2006:62-63.

［7］GJB 4696—1995.海军导弹装备质量监控要求-通用要求［S］.北京:总装备部军标出版发行部，1995.