基于螺栓结合面阻尼特性的分析与研究
陈水胜,胡 海,华中平
(湖北工业大学机械工程学院,湖北 武汉430068)
机械结构中广泛存在的结合面使得机械结构不再连续,使得研究结合面变得复杂.研究结合面的方法很多,主要涉及两个方面:宏观研究和微观研究.宏观研究通常是用弹簧和阻尼器模型来建立振动系统的结合面模型.弹簧的刚度即为结合面的接触刚度,而阻尼器的阻尼值即为结合面的接触阻尼;而微观研究是通过分析结合面变形的物理机理和内阻尼特性来得到结合面的特性.
螺栓连接是机械结构中最主要的零部件连接方式,有研究表明,由连接结合面所产生的能量耗损可以高达机器总能量耗散的80%~90%,而材料本身所产生的能量耗损仅为总耗能的10%~20%[1].研究螺栓连接结合面的能量耗损机理,对于正确认识机械结合面的阻尼特性有重要意义.由于结合面阻尼会使输入的能量产生部分损失,分析载荷与能量损失的关系成为识别结合面阻尼的一条新思路.
1 螺栓结合面阻尼产生机理分析
阻尼通常是指耗损振动能量的能力,也就是将机械振动的能量转变成热量或其它形式的可以耗损的能量.通过对阻尼特性规律的研究,可以提高机械装置的稳定性和抗振性,乃至提高机械结构的整体性能.
结合面阻尼特性与结合面承载力有关,这些作用力的状态可以是静态的、也可以是动态的;其方向可以是法向力、切向力;可以产生弯矩、扭矩或者它们之间的组合.分析与研究结合面阻尼的机理可以从以下两个大的方面加以分析.
1)结合面间的介质.此时可以分为两种情况,一种是两结合面直接接触,直接接触的结合面,阻尼主要是由两结合面相对移动导致的能量损失引起;另一种是两结合面被介质隔开,不直接接触的结合面,产生阻尼的主要原因跟介质的特性有关(如果介质是油,那么产生阻尼的原因是油的粘性.),次要原因是微凸体的塑性变形.
2)结合面间的变形.两结合面接触实际上是微凸体的接触,当结合面平均接触压力较小的时候,结合面间就会产生宏观上的移动,摩擦的存在会损耗部分能量.当面压较大时,结合面间的接触点合并为大的接触点,发生弹性变形,继续增加压力,接触面的材料会因为达到屈服强度发生塑性变形,微凸体的塑性变形有切向的,也有法向的,无论是切向还是法向都会引起阻尼特性.在交变力作用下,法向变形明显小于切向变形.大量试验表明,如果对材料反复加载和卸载,其应力—应变曲线会成为一个滞后回线,此回线所围的面积表示一个循环中单位体积的材料以热能形式耗散掉的能量,这种阻尼又称为滞后阻尼[2],它是结合面阻尼产生的一个很重要的原因.
2 影响结合面阻尼的主要因素
通过对结合面阻尼产生机理的分析,发现影响结合面阻尼的因素很多,主要体现在:
1)结合面之间的压力
如果表面粗糙度和结合面面积不变,所受压力较大的结合面阻尼总大于压力小的结合面阻尼,因为在没有油膜的情况下,结合面相互接触的实际是微凸体,微凸体分布是随机的,并且高度不一样,随着压力增大,接触点数多,微凸体会发生弹性或者塑性变形,耗损部分能量,表现出阻尼特性.
2)结合面间的表面粗糙度
在结合面面压一定情况下,表面粗糙度大的结合面阻尼总小于粗糙度小的结合面阻尼.两个接触表面实际接触的微凸体较少,从而能发生微观相对滑动的微凸体数目少,由此产生的微观摩擦力小,因而阻尼也小.
3)结合面的分维
分维增大时,结合面间的光滑度也变大,实际接触的微凸体数目会因为微凸体密度大而增加,即使压力不变,这时微凸体发生弹、塑性的数目多,能量耗损比较大,阻尼也大,阻尼特性表现明显.
4)结合面间的接触面积
只要粗糙度和结合面间的压力不变,结合面积大的结合面间的阻尼总是大于结合面积小的,因为参与接触的微凸体增加,发生塑性变形的微凸体数目概率加大,消耗的能量多,阻尼也大.
此外,结合面上的材料或材质、结合面的加工方法、结合面的形状、结合面的结合状态(面压分布)、结合面处的动态力等对结合面阻尼都有一定影响,这些影响因素因实际情况的不同而定.
3 建立螺栓连接结合面模型
3.1 建立结合面模型
本文以最为常见的两平板工件的螺栓连接为研究对象,建立了螺栓连接的结构简图(如图1).图中F0为横向载荷,L为两板接触长度.

图1 螺栓连接结构简图
图1 具有对称性,取图1的右半部分为研究对像.之前为了简化计算,认为在预紧力作用下结合面上的压力均匀分布,没有很好反映螺栓连接的实际情况,为此引入真实结合面连接特性的分布参数模型,结合面间的压力随着与螺栓距离的增加而减小,最大值出现在靠近螺栓的部位.如图2(虚线为简化处理时,结合面压力分布均匀的情况,曲线为实际情况下的压力分布情况).

图2 螺栓连接分布参数模型
3.2 建立平衡方程及边界条件
分布参数模型中有粘滞区和滑移区[3],在分布压力作用下,当所受横向载荷较小时,不足以克服因压力产生的摩擦力,两平板没有发生相对移动,称为粘滞区;当横向载荷较大时,两平板会发生微观上的移动,称为滑移区.根据分布参数模型,建立力的平衡条件和位移的平衡条件方程.
1)在粘滞区0≤x≤ln,因为没有滑移发生,所以应有

由平衡方程和边界条件得

其中Ua(x)、Ub(x)和分别为上下表面在位置x处的位移,Ua"(ln)、Ua(x)#,Ub"(ln)、Ub(x)#分别是Ua(x)、Ub(x)的一阶和二阶导数.E 为材料的杨氏模量;A是接触区域的面积;P(x)是结合面0≤x≤ln范围内单位长度上的力分布函数;Fn是x=ln处的内力.
假设上下两板的材料参数和结构参数完全相同,因此两板同一位置处的轴向相互作用力应相等.在粘滞区0≤x≤ln有:
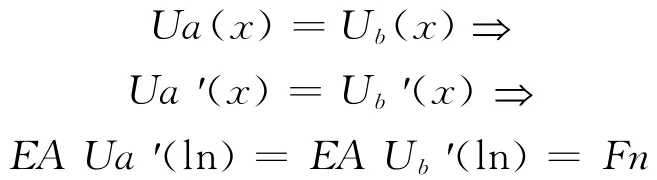
在x=ln处上下两板的位移关系满足

2)在滑移区ln≤x≤L,由图2上下两板的受力分析,可知存在下述关系
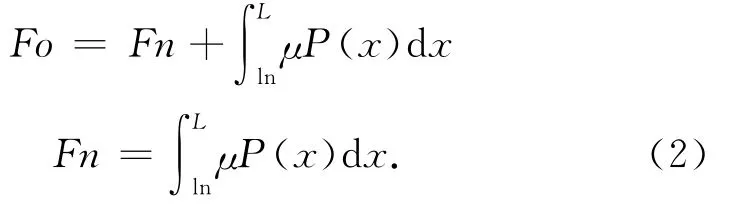
由(2)两式可得
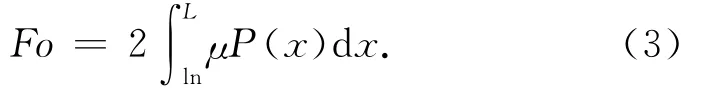
其中μ为库仑摩擦系数.将(3)代入(1)可得

所以上下两板在滑移区的平衡方程和边界条件分别为:
上板平衡方程和边界条件:
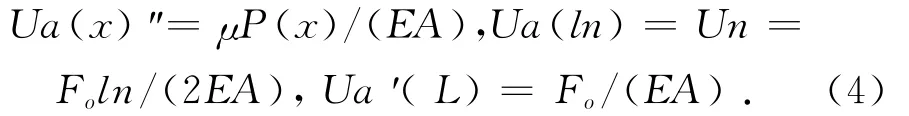
下板平衡方程和边界条件

当压力分布函数P(x)已知时,方程组(4),(5)便可以求解.因此,由能量计算公式:

式中,U(x)为滑动的位移.
可得到螺栓连接结合面产生的能量损失为:

从表达式中可以看到能量损失与载荷、接触面积、摩擦系数、滑动位移等有关,为避免损失过多的能量,可以依实际工况合理选择螺栓组件的规格尺寸、螺栓连接孔的配合尺寸、螺栓连接的结合面积、螺栓连接的预紧力等工作参数.
[1] 傅俊庆.机械连接接口动力学模型研究现状[J].长沙交通学院学报,2004(3):58-64.
[2] 师汉民.机械振动系统[M].第二版.武汉:华中科技大学出版社,2004:27-35.
[3] 王智渊,姚运萍.机械结合面参数识别及其装配性能预测[D].兰州:兰州理工大学图书馆,2010.