旋转平台点云数据的配准方法

周朗明，郑顺义，黄荣永

武汉大学 遥感信息工程学院，湖北 武汉430079

1 引 言

近年来，三维扫描测量技术发展迅速，在逆向工程、文物保护、美容修复、工业测量等方面具有广泛应用。在实际应用中，为了获得物体表面完整的三维点云需要多角度对被测物体进行扫描，进而需要将多视点云配准到统一的坐标系下［1］。点云配准技术有手动配准、依赖仪器配准和自动配准［2］。比较常用的是后两种方法：依赖仪器配准是通过硬件之间的坐标关系将多片点云旋转平移到统一的坐标系下，该方法不需要点云之间具有共同特征，配准速度快，但要求对硬件进行精确标定或者需标志点的辅助，通过对物体表面的标志点编码特征及空间特征进行检测、匹配，获得全场各拍摄图像之间的坐标变换关系［3］；自动配准是通过一定的算法或统计规律将两片云之间的错位消除，该方法需要两片点云之间具有共同特征，在某些情况下需要一些人工干预获取初始值，且配准算法存在一些退化的情况。点云的自动配准大多基于文献［4］提出的最邻近点迭代方法（iterative closest point，ICP）。该方法以四元数配准算法为基础，运用Faugera和Hebert提出的方法计算新的最近点集，再通过迭代选择对应点的方法计算满足对应点之间的距离误差最小条件的旋转和变换矩阵［5－6］.

在依赖仪器配准的技术中，使用标志点进行拼接的方法比较多，多用于大型物体的三维量测，但是对于小型物体，由于其表面面积较小，曲率半径小，导致标志点变形大使得配准精度较低［7］。另外一种依赖仪器配准的技术是使用旋转平台，大部分旋转平台主要是应用于计算机视觉中的轮廓 线 重 构（SFS）方 法［8－9］或 序 列 影 像 重 构 方法［10－14］，而这些方法中对旋转平台进行标定的方法一般从影像中提取标定块的特征平面，根据平面相交于旋转轴的约束条件进行参数的求解［15］，这样就多了一步特征提取的工作并且还需要对相机进行标定。

本文提出的旋转平台点云数据的配准方法是从扫描仪获取的三维点云数据为基础，不需要提取标定点或标定块的几何特征，基本原理是通过标定获取旋转平台坐标系（turntable coordinate system，TCS）相对于扫描仪坐标系或相机坐标系（camera’s coordinate system，CCS）的位置［16］，其实现过程是首先利用圆柱体标定块的表面点云均位于柱面上的这一数学约束，对旋转平台进行标定，获取旋转平台在扫描仪坐标系中的精确位置，并根据旋转角度构建旋转矩阵，然后对置于旋转平台上的扫描物体的点云进行旋转变换，实现多片点云的自动配准。

本算法免除了常用的点云配准算法中标志点粘贴和提取的工作，也不需要在点云后处理软件中进行手动的ICP配准，只需对旋转平台进行一次标定。在扫描仪同旋转平台的相对位置关系没有发生的变化的情况下，能快速地配准置于该旋转平台上的扫描物体点云，提高了点云处理的效率。配准精度高于标志点拼接以及ICP拼接的精度，能较好地解决纹理缺乏的旋转体，如青瓷花瓶、牙齿模型等物体的点云配准问题，而且算法的适用性较高，可稍加改造应用于激光或结构光等三维扫描系统中。

2 算法原理

将物体放置于旋转平台上进行三维扫描，多片点云之间仅有旋转关系，该关系可以通过旋转平台的旋转轴和旋转角度来表达。只要物体的旋转关系已知，就能够根据空间坐标系的变化情况将不同视场的数据整合到同一坐标系下［17］。

对放置于旋转平台上物体进行旋转扫描，此时可视物体绕旋转平台的轴进行刚性变换，利用平台标定过程后得到的旋转轴参数以及旋转的角度，可构建多片点云之间的旋转矩阵，将旋转矩阵同当前片点云相乘，便可将多片点云配准到同一坐标系，也就实现了旋转平台上物体表面点云的自动配准。

为对旋转平台进行标定，使用高为100mm、半径为40mm的圆柱体标定块（以下简称标定块，如图1），基本原理是扫描不同角度标定块表面多片点云数据，然后根据这些点云均在圆柱体表面的约束条件求出标定参数初始值并列出误差方程，迭代求解出表达旋转平台在扫描仪坐标系中位置的标定参数。

图1 标定块实物图Fig.1 Calibration block

2.1 参数说明

旋转平台的标定原理如图2所示，其中D—XYZ是扫描仪坐标系。设旋转平台中心轴单位方向向量为N＝［NxNyNz］，且在旋转平台中心轴上取一点S＝［XDSYDSZDS］作为旋转平台的中心，S与N共同确定了旋转平台的轴；同理设标定块中心轴的单位方向向量为n＝［nx nynz］，且在标定块中心轴线上选取一点Q＝［XDQYDQZDQ］作为标定块的中心，Q与n共同确定标定块的轴。

图2 旋转平台标定Fig.2 Calibration of turntable

2.2 建立模型

假设初始位置处标定块表面，如图2所示（不包括上底和下底，下同）有一点C0在D—XYZ坐标系中的坐标为C0＝［X0DCY0DCZ0DC］。旋转平台由初始位置逆时针转动θ角后，测得C0点在当前点云中的坐标为C＝［XDCYDCZDC］，则C与C0的坐标存在如下变换关系

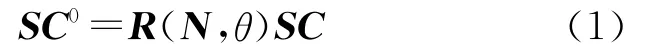
式中

R（N，θ）为旋转变换矩阵，可视为方向向量N及相邻片点云间旋转角度θ的函数，其形式为

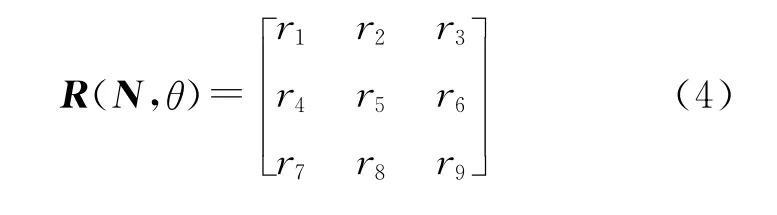
式中

式中，i表示旋转次数。

式（1）中旋转矩阵R表示旋转角度为θ的两片点云之间的旋转关系，利用该式将任意角度扫描的点云数据通过旋转变换到初始位置处，这样不同视场的点云便整合到同一视场中。在式（1）中除点云坐标C与C0已知外，其余参数均未知，标定的目的即求解出这些参数然后根据式（5）构建旋转矩阵。

利用标定块表面点云数据均位于圆柱表面上这一约束条件，在初始位置处，标定块表面点云数据满足如下关系式

式中，n＝ ［nxnynz］为圆柱体中心轴的单位方向向量；rd为圆柱体半径。

将式（1）、式（2）代入式（6）中可得

若记

代入B、Q，将式（7）中的叉积项n×（B－Q）转化为点积项，并将等号两边的项进行平方操作，得到

式中

展开式（8），得到

式中，M＝M′TM′，单位方向向量Nx、Ny、Nz和nx、ny、nz均可用两个角度来表达

由于旋转平台中心轴及标定块中心轴上的定点可以取轴上的任意一点，根据扫描仪同旋转平台的位置特点可将YDP、YDS取为定值0。综合以上条件，可将式（9）中的未知参数显示出来并记F为

式中，已知量为：①当前片点云相对于初始位置转动的角度θ，可从步进电机中读取；②C点坐标，从点云数据文件中读取。未知量为：①旋转平台的中心轴，表达元素为XDS、ZDS、α、β；②标定块在初始位置处的中心轴，表达元素为XDP、ZDP、αn、βn；③标定块半径，表达元素为rd。

2.3 误差方程

对于标定块表面点云任一点均可列出式（10）所示的方程。该方程为非线性方程，为求得未知量解需进行一阶的泰勒展开［18］。得到其线性形式如式（11）

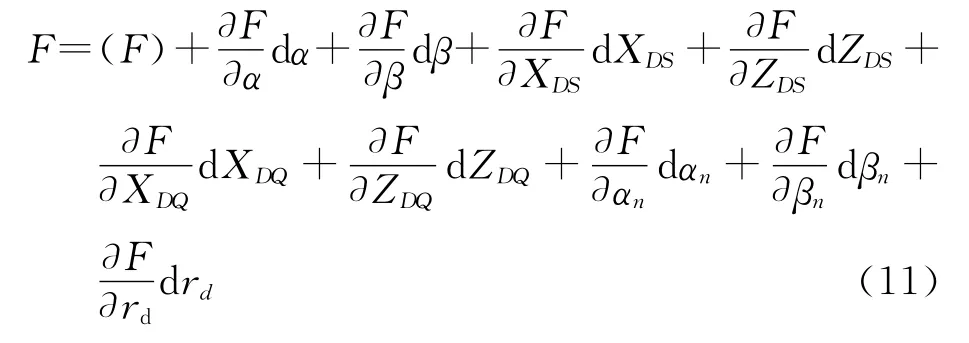
记改正数dα～drd之前的系数分别为a1～a9，则对标定块表面点云位于柱面上的任一点，均可列出如下误差方程

式中

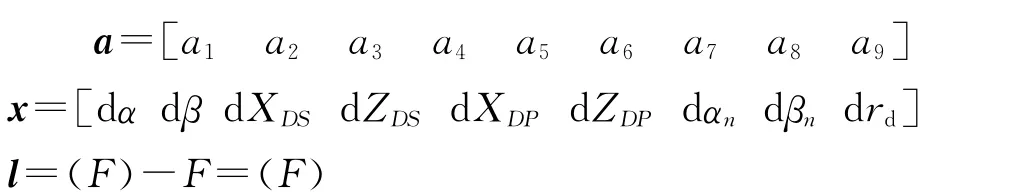
对n（n＞＝9）个点，可列出误差方程组

式中

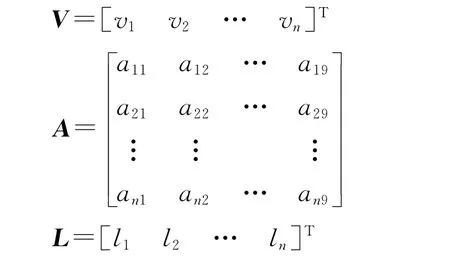
根据最小二乘间接平差原理，可列出法方程式为

式中，n为参与计算的点的个数；P为观测值的权矩阵，反映观测值的量测精度。

由式（14）求得改正数的最小二乘解为

2.4 未知数初值求解

在进行迭代求解时，良好的初值是必须的且有助于快速收敛。式（10）中未知量的部分初值可根据空间点位于圆柱表面的约束条件求出，假设某空间点位于圆柱表面，则其需满足如下方程

式中，X＝［xyz］T表示空间点的三维坐标；T＝［txtytz］T表示圆柱体的中心轴上的某个定点，即式（10）中的［XDQYDQZDQ］；R为圆柱体半径

将式（16）展开可得

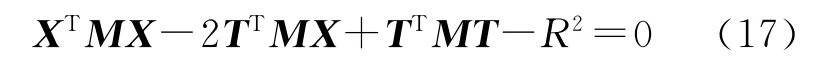
式中

若记矩阵

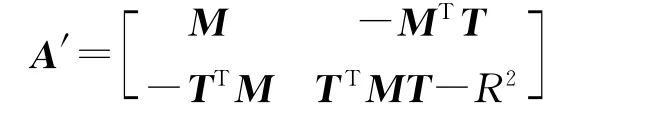
在矩阵A′中，将各分块矩阵M、－MT、TTMTR2均视为独立的变量来求解，按以下方法可以求解出标定块中心轴的方向向量、标定块半径R和旋转平台中心轴方向向量的初值：

（1）方向向量［nxnynz］为A′矩阵中分块矩阵M最小特征值对应的特征向量；

（2）半径可根据矩阵TTMT－R2来求解；

（3）在初值求解部分可认为旋转平台中心轴方向向量和标定块中心轴方向向量平行。

标定块中心轴上的定点可通过将柱面的点投影到平面nxx＋nyy＋nzz＝0上，然后根据投影点拟合一个圆心，初始位置处点云的圆心可作为未知量XDQ、YDQ、ZDQ的初值。

由于标定块是绕旋转平台中心轴旋转，于是利用多片标定块中心轴上的定点通过圆心拟合的方式可以求得旋转平台中心轴上定点XDS、YDS、ZDS的初值。

3 标定过程

旋转平台标定过程如下：

（1）将标定块放置于旋转平台中，设定初始位置，调整扫描仪的位置，使其能扫描到标定块表面数据。

（2）设定旋转平台转动角度（45°）及扫描次数（为了稳定的求解方程应不少于3次，设为5次），旋转平台每旋转到设定角度，即利用扫描仪获取一片标定块表面的点云数据，总共获取到6片点云，点云数据以坐标（x，y，z）的形式记录。

（3）任取其中一片点云的坐标数据，代入到式（16）中，求解出标定块中心轴的方向向量初值［n0xn0yn0z］，标定块半径初值r0d，旋转平台中心轴方向向量初值［N0xN0yN0z］，标定块中心轴定点初值［X0DQY0DQZ0DQ］，旋转平台中心轴定点初值［X0DSY0DSZ0DS］。

（5）遍历第（2）步中的所有片点云数据，按照式（13）列出改正数方程组，代入第（3）步中求得的未知数初值，计算误差方程式的系数和常数项，根据式（14）计算法方程的系数矩阵和常数项

（6）设未知数改正数的初值均为1.0，按照式（15）求出未知数改正数，并与未知数初值求和得到未知数新的近似值，将未知数改正数与规定的限差进行比较，直到小于限差终止迭代，得到9个未知数的精确值，在进行迭代运算时，为了收敛的稳定性需要降低粗差点的影响，因此将式（15）中的观测值权矩阵P按照丹麦法选权迭代法进行设置［19］。

（7）从9个精确值中提取同旋转平台位置相关联的参数为旋转平台中心轴方向向量N＝［NxNyNz］和旋转平台中心S＝［XDSYDSZDS］，保存以上参数到配置文件以待点云配准的需要。

4 配准过程

旋转平台经过标定之后，即确定了其在扫描仪坐标系中的位置，在同扫描仪的相对位置未发生变化的情况下，无需再进行标定，可直接用于点云配准操作，配准步骤如下：

（1）读取参数，读取标定参数旋转平台中心轴方向向量N和旋转平台中心S。

（2）扫描物体，将待扫描物体放置于旋转平台中，根据物体复杂程度和精度要求设定转动角度及转动次数，物体越复杂精度要求越高，则需要更小的转动角度和更多的转动次数，设当前设定的转动角度为θ，转动次数为k，进行扫描将获取到k＋1片点云。

（3）配准点云，记录第i片云相对于初始点云（未旋转之前的位置处）的角度iθ，将角度参数传入到式（5）构建旋转矩阵R。设在第i片点云中任取一点坐标为［xiθyiθziθ］，其配准到初始点云后的坐标为［x0iθy0iθz0iθ］，其转换关系如下

根据式（18），将除初始点云外的所有片点云变换到同一视场中，即完成了点云的配准。

5 试验结果

试验采用了武汉锐智科技公司生产的一款双目结构光扫描仪作为点云扫描设备，其点云标称精度为1／10 000，点距约为0.2mm［20］，将旋转平台加入到该扫描系统中，硬件布置如图3所示。

扫描仪距旋转平台中心距离为65cm，旋转平台的直径为10cm，平台的旋转依靠内部的步进电机驱动，其角度的标称精度为0.075′。为了考察针对旋转平台点云数据的配准精度，设计了如下试验，对如图4（a）所示的贝多芬头像进行了3种拼接操作：ICP手动拼接、标志点拼接以及旋转平台拼接，通过计算多片点云重叠区域的最邻近点对距离的平均值、中误差以及统计处于不同距离阈值的点对比例用于评估多片点云间的拼接精度［21］。其中ICP手动拼接是利用点云后处理软件PolyWorks［22］的拼接模块Align完成的，标志点拼接是利用锐智公司的扫描软件Scanner完成的［20］，标志点为黑色的圆形标志，贴于物体表面。

图3 结构光扫描仪和旋转平台Fig.3 Structured light based scanner and turntable

图4 头像试验Fig.4 Test of avatar

围绕着贝多芬头像（图4（a））进行了9次扫描（点云编号为0～8），相邻扫描角度为30°，按扫描顺序对0－1、1－2、2－3等相邻片点云进行拼接后重叠点云区域的最邻近点对距离进行统计，如图4（b）所示，灰色区域表示两片点云的重叠区域，不同方法拼接精度如表1～表3所示。

表1 ICP手动拼接精度Tab.1 Accuracy report of ICP registration mm

表2 标志点拼接精度Tab.2 Accuracy report of marker based registration mm

表3 旋转平台拼接精度Tab.3 Accuracy report of turntable based registration mm

将以上3种拼接方法得到的平均距离和距离中误差利用折线图表示如图5所示，可以看出，本文提出的针对旋转平台点云数据的配准精度与ICP拼接以及标志点拼接精度相当。

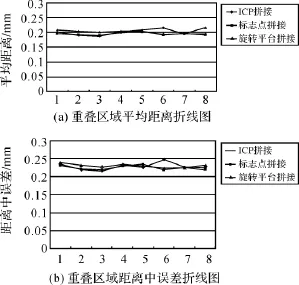
图5 平均距离和距离中误差Fig.5 Polygram of mean distance and error distance

利用本文所提出的配准方法获取的贝多芬头像表面点云结果，如图6所示。加上标定所耗费的时间，扫描整体点云结果不超过5min，点云拼接精度同使用标志点和ICP拼接相当，且整个过程无需人工干预，高效且自动化。

图6 三维贝多芬头像模型Fig.6 3Dmodel of avatar of Beethoven

6 结 论

本文介绍了一种针对旋转平台点云数据的配准方法，不同于其他依赖仪器的匹配方法需要贴标志点，该方法仅需要利用圆柱体标定块对旋转平台位置进行标定即可，标定算法数学模型严密求解过程稳定性高，配准精度同后续ICP拼接或标志点拼接精度相当。可与激光扫描仪，结构光扫描仪，双目立体视觉系等系统配合，扫描完整的物体表面点云数据非常方便快捷，硬件成本较低，自动化程度高，非常适用于小型零件、玩具公仔、馆藏文物等旋转物体的快速三维建模，具有很强的实用价值。

［1］ LISKA C，SABLATNING R.Adaptive 3DAcquisition Using Laser Light［C］∥Proceedings of Czech Pattern Recognition Workshop.Praha：［s.n.］，2000：111－116.

［2］ DAI Jinglan，CHEN Zhiyang，YE Xiuzi.The Application of ICP Algorithm in Point Cloud Alignment［J］.Journal of Image and Graphics，2007，12（3）：517－521.（戴静兰，陈志杨，叶修梓.ICP算法在点云配准中的应用［J］.中国图象图形学报，2007，12（3）：517－521.）

［3］ MA Yangbiao，ZHONG Yuexian，ZHENG ling，et al.Design and Recognition of Coded Targets for 3－D Registration［J］.Journal of Tsinghua University（Sci＆Tech），2006，46（2）：169－175.（马扬飚，钟约先，郑聆，等.三维数据拼接中编码标志点的设计与检测［J］.清华大学学报：自然科学版，2006，46（2）：169－175.）

［4］ BESL P J，MCKAY N D.A Method for Registration of 3D Shapes［J］.IEEE Transaction on Pattern Analysis and Machine Intelligence，1992，14（2）：239－239.

［5］ NATASHA G，LESLIE I，RZYMON R，et al.Geometrically Stable Sampling for the ICP Algorithm［C］∥Proceedings of International Conference on 3DDigital Imaging and Modeling.Banff：［s.n.］，2003：260－267.

［6］ ZHENG Dehua，YUE Dongjie，YUE Jianping.Geometric Feature Constraint Based Algorithm for Building Scanning Point Cloud Registration［J］.Acta Geodaetica et Cartographica Sinica，2008，37（4）：465－468.（郑德华，岳东杰，岳建平.基于几何特征约束的建筑物点云配准算法［J］.测绘学报，2008，37（4）：465－468.）

［7］ ZHANG Yanli，LI Xiaoxing，YANG Ying，et al.Rotate Registration of Small Workpiece［J］.Aerospace Manufacturing Technology，2005，2（1）：32－36.（张艳丽，李晓星，杨兴，等.小型零件测量的旋转拼接［J］.航天制造技术，2005，2（1）：32－36.）

［8］ MULAYIM A Y，ULAS Y，ATALAY V.Silhouettebased 3DModel Reconstruction from Multiple Images［J］.IEEE Transactions on Systems，Man and Cybernetics－Part B，Special Issue on 3DImage Analysis and Modeling，2003，33（4）：582－591.

［9］ ZHENG Shunyi，ZHOU Langming，LI Cailin，et al.Automatic 3DModel Reconstruction of the Diamond［J］.Measurement，2012，45（5）：844－855.

［10］ FREMONT V，CHELLALI R.Turntable Based 3DObject Reconstruction［J］.IEEE Conference of Cybernetics and Intelligent Systems，2004，2：1277－1282.

［11］ BEARDSLEY P A，TORR P H S，ZISSERMAN A.3D Model Acquisition from Extended Image Sequences［C］∥Proceedings of European Conference on Computer Vision.［S.l.］：ECSCW，1996：683－695.

［12］ FITZGIBBON A W，CROSS G，ZISSERMAN A.Automatic 3DModel Construction for Turn－Table Sequences［C］∥Proceedings of 3DStructure from Multiple Images of Large－scale Environments SMILE98.Freiburg：［s.n.］，1998：154－169.

［13］ EISERT P，STEINBACH E，GIROD B.Automatic Reconstruction of Stationary 3DObjects from Multiple Uncalibrated Camera Views［J］.Circle System Video，2000，10（2）：261－271.

［14］ SAWHNEY H S，OLIENSIS J，HANSON A R.Image Description and 3DReconstruction from Image Trajectories of Rotation Motion［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1993，15（9）：885－898.

［15］ CARLO C，DARIO C，ALBERTO D.A Desktop 3D Scanner Exploiting Rotation and Visual Rectification of Laser Profiles［C］∥Proceedings of IEEE International Conference on Vision Systems.［S.l.］：IEEE，2006.

［16］ PARK S Y，SUBBARAO M.A Multiview 3DModeling System Based on Stereo Vision Techniques［J］.Machine Vision and Application，2005，16：148－156.

［17］ LONG Xi，ZHONG Yuexian，LI Renju，et al.3DSurface Intergration in Structured Light 3DScanning［J］.Journal of Tsinghua University（Sci＆Tech），2002，42（4）：477－480.（龙玺，钟约先，李仁举，等.结构光三维扫描测量的三维拼接技术［J］.清华大学学报：自然科学版，2002，42（4）：477－480.）

［18］ DAVID A.Computer Vision：A Modern Approach［M］.London：Prentice Hall，2004：153－154.

［19］ LI Deren，YUAN Xiouxiao.Error Processing and Reliability Theory［M］.Wuhan：Wuhan University Press，2002：241－242.（李德仁，袁修孝.误差处理与可靠性理论［M］.武汉：武汉大学出版社，2002：241－242.）

［20］ 武汉锐智.三维摄影扫描系统（PhotoScanShop）［EB／OL］.［2011－04－23］.http：∥ www.ruizhivm.com.cn／product＿1.htm

［21］ SEITZ S M，CURLESS B，DIEBEL J，et al.A Comparison and Evaluation of Multi－view Stereo Reconstruction Algorithms［C］∥Proceedings of International Conference on 3DDigital Imaging and Modeling.Banff：IEEE Computer Society，2003：260－267.

［22］ Innovmetric Soft.Polyworks V11 ［EB／OL］.［2012－01－12］.http：∥www.innovmetric.com／polyworks／3D－scanners／home.aspx？lang＝en