不确定性条件下建设工程设计进度优化研究

陈建国， 田宏伟

(同济大学 经济与管理学院， 上海 200092)

在复杂建设工程设计项目中，往往是由来自多个设计部门的多专业设计队伍共同完成整个设计任务。这种多专业的合作框架下，每一个专业设计团队对设计做出的改变都会对其他专业的设计产生一定的影响，需要多次反复修改与协作，才能获得最优设计结果。这种反复导致设计过程中存在不可避免的重复工作的危害，即迭代问题的产生。英国学者Latham的研究表明，建筑产业内重复、重叠的工作和各专业间的信息交流的不畅使得整个项目浪费了30%的花费[1]。因此，如何识别和处理这些迭代问题，成为当前复杂建设工程设计进度管理优化的关键。传统的进度计划工具如横道图、CPM、PERT等由于自身的缺陷，难以描绘出活动间的迭代反馈关系。

当前的规划实践很少考虑建筑设计过程的跨专业及迭代性，导致在设计和施工阶段的时间和成本协调中出现设计过程的返工问题，而以DSM为核心的ADePT技术则可以有效解决这类问题[2]。Chua等[3]从信息流动和信息结构层次的角度进一步扩展ADePT的工作流，提出了设计流程管理的PPI模型。Fayez等[4]通过对比CPM与DSM在设计建设领域中的应用，认为传统的关键路径法(CPM)不能有效处理设计中联结的工序，而设计结构矩阵的方式可以直观地表现信息流及项目的工作流程。针对AEC行业当前大多数过程建模工具不能分析迭代信息循环的问题，Pektas等[5]建立了基于参数化设计结构矩阵的过程建模和系统分析工具，为建筑设计管理提供了新的方向。Qian Shi等[6]运用DSM方法研究了进度计划过程中的不确定性问题，但未将返工纳入研究范围。我国部分学者对DSM在建筑产品协同设计[7,8]及项目进度管理方面[9,10]的应用进行了相关研究，设计进度优化领域的应用研究关注较少。针对活动工期的不确定性，部分学者引入蒙特卡洛模拟技术，基于网络计划图设置计算规则，通过仿真预测项目总工期的分布及可能的关键线路，为后续的进度计划及控制提供科学依据[11,12]，但均未考虑耦合或返工情况下的工期仿真。

开发过程中存在的迭代与反复现象造成开发总量和开发过程的不确定[13]，复杂建设工程项目设计过程中易发的迭代问题也给设计进度管理带来了一定的不确定性。但是，已有的研究对复杂建设工程项目设计阶段的进度管理关注较少，很少涉及带有迭代的设计过程的进度优化，对不确定性条件下设计进度的优化研究就更为缺乏。因此，本文尝试将DSM理论引入到复杂建设工程设计进度管理领域，用于应对设计过程中的迭代问题，同时，运用蒙特卡洛模拟方法对设计进度的不确定性进行研究，探索不确定性条件下复杂建设工程项目设计进度的优化问题。

1 DSM的基本概念

设计结构矩阵(Design Structure Matrix，DSM)是一种可以反映作业之间关系的方阵，通过它的行和列可以清晰地描述项目所有作业之间的信息流关系，恰好弥补了传统设计进度管理技术仅能处理工作流的缺陷。DSM中，行列元素均以相同的顺序排列在最上方和最左侧，如果两元素间有关系，则对应位置予以标记，否则不做标记，对角线单元没有意义。矩阵的行表示所有其他活动对所在行活动的信息输入，矩阵的列表示所在列活动对所有其他活动的信息输出。由此可以看出，下三角矩阵表示信息前馈交流，即来自前期任务的信息可以为后续的任务所利用；上三角矩阵表示信息反馈交流，揭示设计迭代的过程，即后期任务产生的信息可能会导致前期任务的返工。信息反馈或者耦合会导致活动的返工，而在设计管理中，信息反馈又是大量存在的，这就需要对初始的DSM进行优化。DSM优化的方法有很多种，比较常用的主要有划分、撕裂和聚类运算。

2 基于DSM的设计进度优化模型

在设计进度管理中，工序作业次序的调整是影响设计进度的关键因素之一。因此，本文从优化工序作业次序的角度出发，构建了基于DSM的设计进度优化模型，如图1所示。

图1 基于DSM的设计进度优化模型

(1)确定主要活动。DSM一般用于研究活动间交互关系较为复杂的设计过程，为了降低模型的复杂性，首先需确定项目的主要组成活动。

(2)初始DSM的建立。运用WBS方法，将主要活动细分为可实际执行的活动，分别列于DSM的行列当中；同时，识别和量化活动之间的信息依赖关系，构造出初始的DSM矩阵。

(3)DSM的优化。设计活动组成的初始DSM中往往存在大量的迭代循环圈，需要运用相关的优化算法对初始DSM进行处理，尽可能使其下三角化。对于无法通过划分处理的迭代循环圈，则可通过撕裂或者聚类的方法将其转化为不存在迭代的DSM。

(4)DSM的仿真。实际工程中，活动的持续时间往往具有不确定性，这种不确定性，很可能导致关键活动或关键线路的改变，因此需要运用仿真的方法，通过大量的模拟实验来预测项目工期的大致分布，为进度计划的编制与控制提供依据。DSM模型中可能存在迭代，也可能不存在迭代，且两种DSM的工期计算方式也存在着明显的区别，这就需对其分别进行仿真研究。

(5)仿真结果分析。通过对结果的分析，可以发现进度控制及优化的方向，为设计进度的管理提供决策支持。

3 基于蒙特卡洛模拟的DSM仿真模型

大型复杂建设工程设计项目往往具有不确定性，每个设计活动的执行时间很难给出确定数值，设计总工期难以判断，给设计进度的有效管理带来了极大困难。传统的处理方式大多是基于双代号网络计划图的仿真，并不能处理存在循环回路的设计过程，为贴近工程实际，本文利用蒙特卡洛模拟方法设计了DSM的仿真模型。

3.1 随机网络模型的建立

复杂建设工程设计项目往往包括大量的子项目，这些子项目可以通过活动之间的信息依赖建立DSM矩阵模型。DSM可看成是网络图的一种形式：设计活动的执行表现为随机网络的推进，各活动可看成网络计划的节点，每个活动接收紧前活动提供的信息，处理后又提供给其紧后活动，同时，它也可以给前序活动提供反馈信息，使前序活动做出相应的修正。因此，也可以对DSM模型进行仿真分析。DSM的仿真必须是基于优化后的DSM模型的仿真，以防止无序的循环而导致仿真无法终止。针对活动持续时间的不确定性，参考文献[14]对PERT进行了简单改进，使其更为符合工程实际。

3.2 无迭代DSM仿真模型设计

划分后的DSM中可能存在迭代循环回路，也可能不存在。对于不存在迭代的DSM模型，称之为“无迭代DSM”；对于存在迭代的DSM模型，称之为“迭代DSM”。无迭代DSM中不存在反馈标志，活动表现为顺序或并行执行，可设计如下的仿真模型。

(1)仿真数据输入。设无迭代DSM共有n个组成活动，每个活动持续时间的乐观值、可能值、悲观值分别存储于O、L、P三个矩阵中；矩阵A对角线用于存储随机产生的对应活动的持续时间，矩阵O、L、P、A均为n行n列；矩阵B为无迭代DSM的布尔型，用于存储活动间的信息依赖关系，即有依赖对应位置用数字“1”表示，无依赖对应位置用数字“0”表示。例如活动i持续时间的乐观值为O(i,i)，可能值为L(i,i)，悲观值为P(i,i)，随机产生的持续时间为A(i,i)，B(i,j)=1则表示活动j向活动i输出信息。

(2)仿真过程设计。为简化模拟过程，此处不考虑相邻两项活动之间的时间间隔以及信息传递时间，且紧后活动须在紧前活动完成后才可以开始。则相关时间参数计算方式如公式(1)：

(1)

式中，ES为最早开始时间；EF为最早结束时间；LF为最迟结束时间；A为活动持续时间；i,j为i表示j的紧前活动，j表示i的紧后活动。

(3)仿真结果统计。通过大量的仿真试验，可以得到项目总工期的大致分布曲线及概率；同时，在仿真过程中通过对关键活动的识别，可以统计出每个活动成为关键活动的次数，从而为进度管理的工作重点提供可靠支持。

3.3 迭代DSM仿真模型设计

在复杂建设工程项目中，经划分算法处理后的DSM中，往往仍然存在大量的循环迭代回路，即“迭代DSM”。对迭代DSM进行仿真时，由于矩阵内部有循环回路，可能会因为仿真进入无限循环而导致整个过程无法结束，因此需对循环回路设置一定的限制条件。考虑学习效应，活动再次执行时，返工时间或返工量会有所减少，为简化计算过程，可以根据问题实际设计相应的学习率Pf，第二次执行时，所需的时间就会减少Pf，并假定返工只发生一次。

(1)仿真过程的改进。相比无迭代DSM，迭代DSM中存在耦合活动集(循环迭代回路)，在进行仿真设计时，需在无迭代DSM仿真过程的基础上，增加对耦合活动集的处理。改进措施为：对耦合活动集，考虑学习效应，修正待返工活动的单次执行时间，并更新后续活动所有紧前活动最早结束时间的最大值。

图2 基于蒙特卡洛模拟的DSM仿真模型

(2)仿真流程的设计。迭代DSM一次仿真流程如图2所示。虚线框内为耦合活动集的工期计算过程，计算式中的Pjk代表活动j的学习率；把虚线框中的流程删除，即可得到无迭代DSM项目总工期的一次仿真。

4 某大飞机配套工程设计进度优化

4.1 项目背景

某大飞机配套工程属于典型的复杂建设工程项目，工期要求紧，参与设计单位多，设计流程复杂，在进行设计进度管理时必须首先确定活动的执行顺序，识别出易产生迭代循环的活动，并预判关键线路，保证里程碑事件的按时完成。由于传统的进度管理工具难以处理复杂工程项目中大量的迭代任务，因此，本文以DSM为研究工具，以Project DSM软件为运算平台，探索DSM在复杂建设工程项目设计进度优化领域的适用性。

4.2 基于DSM模型的设计进度优化

某大飞机配套工程包括十一项活动，为简化研究过程，保留对工期有重要影响的七项关键活动予以分析。根据DSM的建立流程，运用WBS方法对活动进行分解，并识别信息输入输出关系，量化活动间的信息依赖关系，如表1所示。绘制分解后的活动组成如表2所示。

表1 信息依赖强度等级

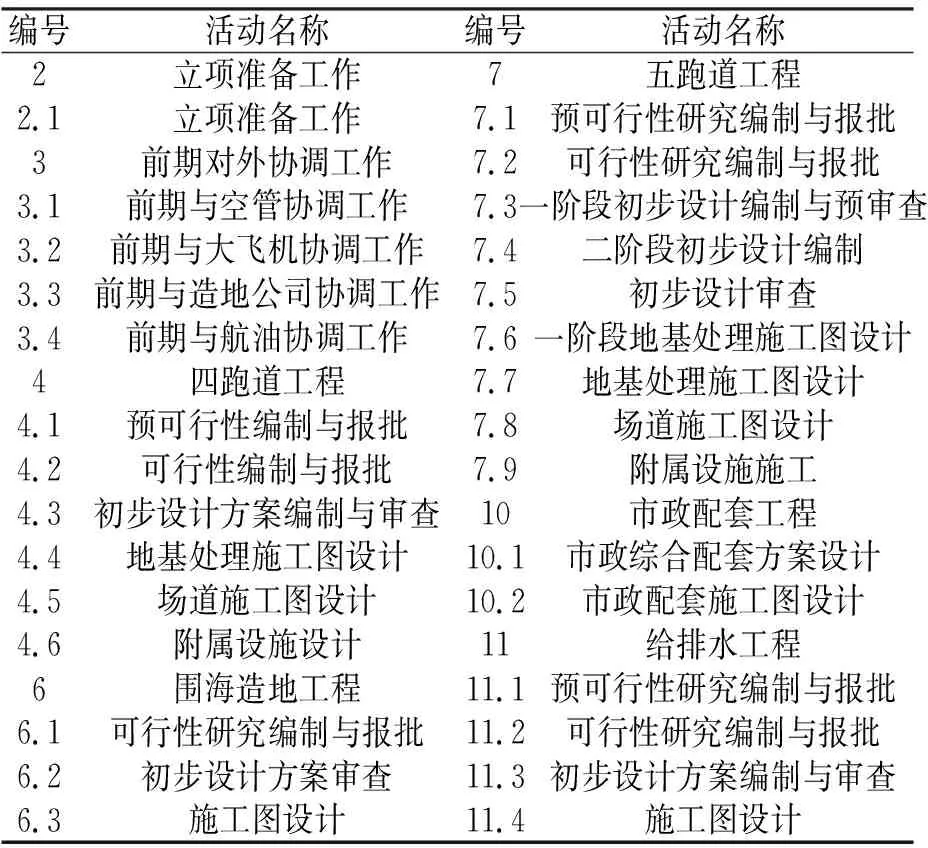
表2 某大飞机配套工程项目活动分解组成

(1)初始DSM的划分。将以上信息输入到Project DSM软件平台，对初始DSM进行划分，可得到划分后的DSM如图3(以十五项子活动示意)所示。划分后的DSM只存在一个较小的设计信息循环圈，循环圈内的六项活动完成后，其余活动只需按照在DSM中从左上到右下的排列顺序执行，不会再出现迭代返工现象。

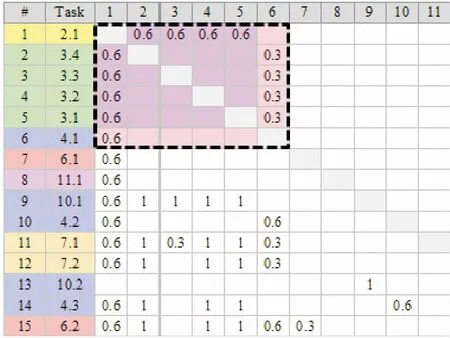
图3 划分后DSM

(2)划分后DSM的撕裂。观察划分后的DSM，活动1～6组成了一个迭代循环圈，一个活动发生改变会引起圈内所有活动的返工。由于各活动并不表现为完全依赖，可运用一定的方法对其信息依赖关系进行撕裂。在Project DSM软件平台上，设置以循环圈最小为撕裂目标，可得到撕裂后的新DSM如图4所示。

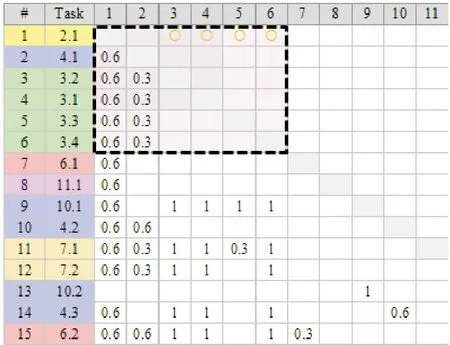
图4 撕裂后DSM

对比图3和图4，划分后的DSM和新DSM仅虚线框标注的范围内活动的排列顺序及约束关系存在差别。新DSM将活动前期与空管协调工作、前期与大飞机协调工作、前期与造地公司协调工作、前期与航油协调工作对立项准备工作的信息约束关系撕裂(如图4中圆圈标注)，使得立项准备工作能够独立开展，不再因为后期工作的执行而返工。撕裂后的DSM完全下三角化，活动四跑道预可行性编制与报批对前期对外协调工作均有影响，因此被提前到仅次于立项准备工作执行。

通过信息的提前发布等方式，运用解耦操作对DSM中的迭代循环活动圈进行撕裂，可以简化活动执行流程，使得活动依次执行下去，不再产生返工现象。而无论是基于项目经验或是传统的网络计划技术，都难以对循环活动进行相应处理。

4.3 不确定条件下工期模拟仿真分析

为实现某大飞机配套工程项目总工期的有效控制，建设方组织相关专家对分解后的二十九项子设计活动持续时间进行研判，并最终给出每个活动的乐观工期(a)、最可能工期(m)和悲观工期(b)。根据建模部分随机网络的确定方法，本文假设各活动的k值均为4，基于MATLAB平台进行仿真实现。

4.3.1迭代DSM工期仿真实现

经划分算法处理后的DSM如图3所示，前六项活动存在迭代循环现象，可按照上文设计的“迭代DSM”仿真模型进行仿真实现。对前六项活动设置返工矩阵C，如表3所示。根据返工矩阵，活动的执行流程为：活动1执行完毕后，活动2、3、4、5、6均可以开始执行，活动2、3、4、5执行完毕均会导致活动1产生60%的返工量；活动6执行完毕会导致活动2、3、4、5产生30%的返工量，进而再引起活动1的返工。为简化计算流程，对迭代循环圈设置如下计算模型：不考虑返工因素，至循环圈中的最后一项活动完成后，执行发生返工的项目，按照返工量更新总最早结束时间，且循环只发生一次。

表3 迭代DSM的返工矩阵

图5 迭代DSM仿真结果

对迭代DSM矩阵，设置仿真次数10000次，统计出的最大总工期为2931.4 d、平均工期为2851.3 d；即若不撕裂循环迭代圈，某大飞机配套工程项目最大总工期为2930 d左右，正常总工期为2851 d左右；总工期的分布如图5所示，完工工期大多位于2840～2860 d之间。这只是考虑一次循环时可能出现的结果，若实际执行时发生了多次循环，则完工工期会更长。

4.3.2无迭代DSM工期仿真实现

上文分析，若不撕裂DSM中的循环迭代圈，项目总工期将达到2851 d左右，难以满足建设方的要求。而采取撕裂操作后，可有效破除活动的迭代循环圈(如图4所示DSM)，使活动能够依次执行下去，不再发生返工。按照上文设计的“无迭代DSM”仿真模型，针对如图4所示的DSM，设置仿真次数10000次，统计出的最大总工期为2618.2 d、平均工期为2530.9 d；活动成为关键活动的次数和概率如表4所示，总工期的分布如图6所示。

表4 无迭代DSM关键活动仿真统计

由表4可知，活动立项准备工作(2.1)、四跑道预可行性编制与报批(4.1)、五跑道可行性研究编制与报批(7.2)、五跑道一阶段初步设计编制与预审查(7.3)、五跑道二阶段初步设计编制(7.4)以及五跑道附属设施施工(7.9)在多次仿真中为关键活动的概率为1，则意味着这六项活动在项目执行过程中肯定为关键活动；前期与大飞机协调工作(3.2)、前期与空管协调工作(3.1)在多次仿真中成为关键活动的概率均超过0.5，则意味着这两项活动极易成为关键活动。由此，可判断在大飞机配套工程项目中，可能的关键线路两条： 2.1→4.1→3.2→7.2→7.3→7.4→7.9和2.1→4.1→ 3.1→7.2→7.3→7.4→7.9，由于活动3.2成为关键活动的概率0.58稍高于活动3.1的0.53，则线路2.1→4.1→3.2→7.2 →7.3→7.4→7.9更易成为关键线路，在进度计划编制及活动执行过程中资源分配时都应予以着重考虑。

根据仿真结果，若大飞机配套工程按无迭代DSM所列的活动顺序执行，则最大总工期为2620 d左右，正常总工期为2530 d左右。管理方可结合完工时间节点的要求，合理安排工作任务，预测活动能否按预定节点完成；如若不能，则需调整关键线路的持续时间，通过推迟非关键活动的开始时间等方法满足关键活动的资源需求，以保证里程碑事件的顺利完成。

4.3.3工期仿真结果说明

对比无迭代DSM与迭代DSM的平均工期发现，撕裂耦合活动集中部分活动间的信息约束关系后，项目的总工期可以节约320 d左右，由此可以看出迭代所引起的返工对项目工期的重大影响。对于迭代DSM，若运用甘特图按照各活动的持续时间可能值(m)进行总工期估算，得出项目的总工期为2471 d，而不是DSM仿真模拟出的2851 d，并低于无迭代DSM的2530 d。这就牵涉到迭代循环圈的问题。

运用Project DSM软件绘制撕裂前DSM的甘特图和撕裂后DSM的甘特图分别如图7和图8所示。图7中，甘特图只能表示活动1～6依次执行下去，并以此计算项目总工期，而未考虑活动4.1对第二三四五项活动均有影响，其执行很可能引起前面四项活动的返工；图8中，撕裂后的DSM对活动顺序又进行了调整，活动4.1被提前到仅次于立项准备工作执行，活动3.1～3.4均在活动4.1完成后才能开始，即将图7中的并行工作改为了串行，从而延长了项目的总工期，使得工期由2471 d延长为2530 d左右。

图7 迭代DSM甘特图示例

图8 无迭代DSM甘特图示例

某大飞机配套工程项目计划2016年底完工，若管理者按照甘特图所示进行总工期预测，则会判定项目于2016年4月4日就可以完工，并以此安排进度计划。由于循环迭代圈的存在，实际总工期可能会比甘特图预测的2471 d要多出380 d，项目最早也要到2017年底才会结束，从而导致进度失控，给业主方造成巨大损失。

通过一定的方式将前期协调工作对立项准备工作的信息约束关系撕裂，则可以解除循环迭代圈，形成无迭代DSM，项目最早可于2016年6月6日左右结束，满足业主方工期要求。当然，信息约束关系不能随意的撕裂，不仅需要考虑约束关系的强弱，还要判断撕裂后的活动是否符合实际的逻辑关系；同时，信息约束关系的撕裂也要求提前发布必要的信息，具体的处理方式则根据项目的不同而不同。

5 结 语

迭代是复杂建设工程设计项目中的多发问题，也是引起工期延长的重要因素，而DSM可以有效识别迭代循环活动；针对设计进度中的不确定性，运用蒙特卡洛模拟方法，可以实现对可能关键线路和完工工期的预测。因此，为解决复杂建设工程项目设计阶段的设计迭代及进度不确定性问题，本文构建了一种以DSM理论为基础，以Project DSM进度管理软件为计算平台的进度优化体系；同时，基于蒙特卡洛模拟方法，建立了不确定性条件下的DSM仿真模型，并将其应用于某大飞机配套工程项目的设计进度管理工作，缩短了项目总工期，对复杂建设工程项目设计进度的优化具有一定的借鉴意义。

[1] 吴子燕. 项目驱动下建筑产品并行设计关键技术研究[D]. 西安：西北工业大学, 2006.

[2] Austin S A, Baldwin A N, Li B, et al. Analytical design planning technique for programming building design[J]. Proceedings of the Institution of Civil Engineers: Structures and Buildings, 1999, 134(2): 111-118.

[3] Chua D K H, Tyagi A, Ling S, et al. Process-parameter-interface model for design management[J]. Journal of Construction Engineering and Management, 2003, 129(6): 653-663.

[4] Fayez M, Axelsson P, Oloufa A A, et al. DSM Versus CPM: Issues for Planning Design & Construction Activities[C]∥Proceedings of the Construction Research Congress, Winds of Change: Integration and Innovation in Construction. 2003: 181-188.

[5] Pekta S T, Pultar M. Modelling detailed information flows in building design with the parameter-based design structure matrix[J]. Design Studies, 2006, 27(1): 99-122.

[6] Shi Q, Blomquist T. A new approach for project scheduling using fuzzy dependency structure matrix[J]. International Journal of Project Management, 2012, 30(4): 503-510.

[7] 杨 劲, 吴子燕, 孙树栋. 建筑工程设计过程规划研究[J]. 系统工程理论与实践, 2005, 25(10): 125-130.

[8] 吴子燕, 覃小文, 刘中峰, 等. 建筑工程并行设计过程规划与仿真研究[J]. 系统仿真学报, 2007, 19(15): 3577-3581.

[9] 白思俊, 万小兵. 基于设计结构矩阵的项目进度周期[J]. 系统工程理论与实践, 2008, 28(11): 51-54.

[10]王 聪, 张广智, 刘敬东. 基于设计结构矩阵的舰船维修工程进度优化模型[J]. 舰船科学技术, 2010,(9): 16-20.

[11]李 强, 张 静, 张耀坦.蒙特卡洛仿真技术在工程进度计划中的应用[J]. 长江大学学报( 自科版) 理工卷,2007,4(2):62-65.

[12]吴正安. 基于MATLAB的水电工程项目工期仿真分析[J]. 水利建设与管理,2011,(8):72-52.

[13]裴小兵, 蒋 伟, 皇甫丹丹. 并行产品开发进度管理研究[J]. 科技进步与对策,2013,30(7):22-25.

[14]文 平. 计划评审技术的改进[J]. 数学的实践与认识,2007,37(21):5-10.