均匀化方法在剪压砌体力学分析中的应用

王 进， 印长俊， 马石城， 张 亮

(湘潭大学 土木工程与力学学院， 湖南 湘潭 411105)

渐进均匀化方法(AHM)是70年代出现的一种从摄动法出发，从细观力学的角度来研究周期性复合材料力学性能的方法，文献[1]给出了一般弹性问题的均匀化控制方程，文献[2]在此基础上推出了二维问题的AHM弹性解，文献[3]应用有限元程序ABAQUS得出了加强体三维问题的数值解，文献[4]以细观力学均匀化为基础得出了砌体的三维弹性数值解并分析了数值解和细观力学模型解相比的误差。为了将AHM应用于工程，文献[5]以均匀化控制方程为基础，通过APDL语言对ANSYS开发了均匀化计算程序AHMP 1.0。传统的砌体结构设计方法是根据试验和工程经验，以概率论为基础的极限状态设计法。传统的方法缺乏系统的理论支持，难以进一步分析受力性能和破坏机理，设计方法也难进一步发展，而直接用有限元分析计算成本太高，难以与工程应用接轨。砌体是由砌块和砂浆按一定的周期性复合组砌而成，引入AHM来研究砌体是目前的一个趋势。

1 均匀化理论及其计算程序

1.1 均匀化理论

如果不考虑单胞的残余应力和体力，3D单胞Y域中的两个控制方程为：

∀v∈VY

(1)

(2)

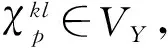
B. Hassani和E. Hinton推导了2D问题的解析解和数值解，本文在此基础上进一步对3D问题进行简单推导。若刚度较大材料和刚度较小材料都是各项同性体，2D问题需要求解3种工况得到等效弹性矩阵D的5个分量；3D问题则需要求解6种工况得到等效弹性矩阵D的12个分量，这6个工况分别是(a：k=l=1)，(b：k=l=2)，(c：k=l=3)，(d：k=2,l=3)，(e：k=3,l=1)，(f：k=1,l=2)，下面将以工况a为例进行分析。

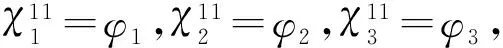
ε(v)=

(3)

ε(φ)=

(4)

(5)

这里ei是弹性矩阵的列向量，i=1,2,3,4,5,6，因此

(6)

将式(3)，式(4)和式(6)代入展开并去掉零系数的式(1)中得到

(7)

同样的，3D情况下，式(2)可以变成

(8)

(9)

(10)

1.2 计算程序

绝大多数的单胞均匀化方程必须采用数值解法，例如有限元法、边界元法、波谱法，本文采用有限元法。参考文献[5]的计算程序，将此程序与砌体三维等效模量的计算接轨。以文献[6]为理论基础，利用APDL语言实现AHM，并分析剪压砌体力学行为包括五步：

(1)建立单胞有限元模型，单胞的选取应考虑周期性和对称性，尽可能的简化几何结构;

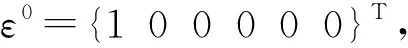
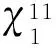
(4)重复(1)～(3)步，求得其它工况下的等效模量矩阵，对于3D问题需要算6次；

(5)根据已求得的等效模量张量定义正交各向异性均匀化材料，建立砌体剪力墙的均匀化有限元模型分析其应力应变状态和破坏机理。

2 算 例

2.1 AHM适用性

本算例是为了验证将AHM应用于砌体三维等效模量的计算是否合理，算例的计算模型各参数以及结果的表现形式与A. Zucchini的相同，只有计算方法不同。A. Zucchini的算例中砖的尺寸为210×100×52 mm3，砂浆灰缝厚度均为10 mm。根据周期性和对称性选取均匀化三维单胞如图1，并建立单胞的笛卡尔右手系，X沿墙长方向，Y沿墙高方向，Z沿墙厚方向。保持砌块的材料特性为常数，而砂浆的材料特性是变化的。令砖的杨氏弹性模量Eb=20 GPa，泊松比vb=0.15；令砖的杨氏弹性模量与砂浆的杨氏弹性模量的比值在1～1000之间变化，即Eb/Em∈[1,1000]，泊松比vm=0.15。

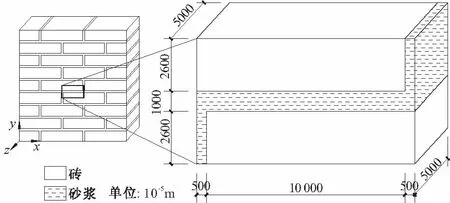
图1 砌体均匀化单胞

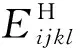
将AHM计算结果以及文献[4]的细观力学模型理论解用曲线的形式表达于图2。图2选列了具有代表性的四个等效模量分量，EH为均匀化等效模量，Eb为砌块的杨氏弹性模量，Em为砂浆的杨氏弹性模量。

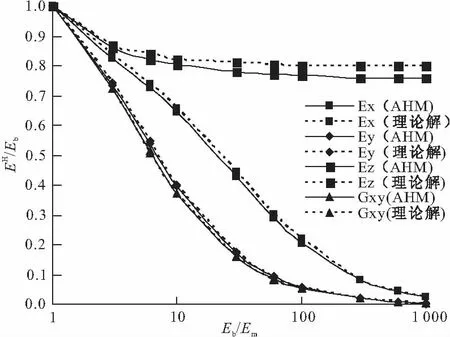
图2 AHM与细观力学模型解的比较

通过对比可见，AHM计算结果与文献[4]细观力学模型理论解很接近，误差均不超过7.032%，说明在下文中应用AHM分析砌体是合理的，同时也说明AHM在砌体结构实际工程中是适用的。

2.2 砌体剪力墙

本例应用AHM分析砌体剪力墙的应力应变状态和破坏机理，首先将砌体剪力墙离散为均匀化单胞，通过2.1节介绍的AHM计算得到单胞的三维等效模量D。然后定义一种新的正交各向异性实体材料：均匀化砌体。将三维等效模量D赋予这种均匀化砌体，在ANSYS平台上建立受平面内剪压复合作用的均匀化砌体剪力墙模型，得到剪力墙的应力应变状态和位移等，并分析砌体剪力墙的破坏机理。与复合界面模型、砌体剪力墙试验[7]的相关结论对比，进而说明AHM分析砌体剪力墙的有效性。

本例基于AHM的有限元模型采用8节点六面体实体单元，剪力墙尺寸为990×1000 mm2，由18皮砖按顺砖砌式砌筑而成，其中，上下各一皮固支在钢梁上，底部钢梁与地面固支，顶部钢梁与地面滑支，如图3。试验中的剪力墙为机制粘土砖，尺寸为210×52×100 mm3，砌筑灰缝厚度均为10 mm。为了模拟实际砌体房屋中某一面墙的受力状态，试验中采取不同的竖向均布荷载p对剪力墙进行预压，然后在剪力墙顶部施加一个单调缓慢均匀增大的水平荷载，该水平荷载采用极限应变控制，保持上下边界只发生水平位移，不允许产生竖向位移。相关材料参数列于表1中。为了模拟上下部可以视为刚体的钢梁，上下部的边界节点被强制产生与钢梁完全相同的竖向和水平位移，在有限元求解器中按线性运算法则、非对称解方案、不考虑砌体失稳进行求解。

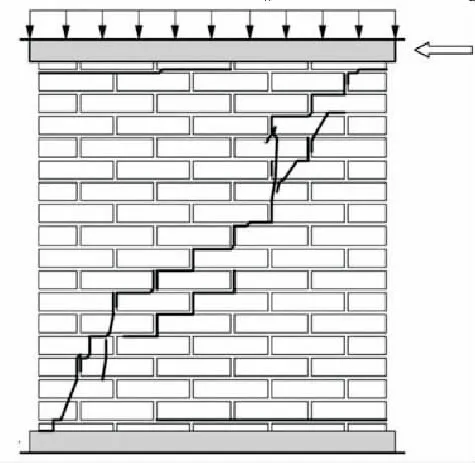
图3 试验剪力墙破坏形态

本文用以对照的砌体剪力墙试验是由Raijmakers 和Vermeltfoort在CUE的架构下进行的[8]。用以对照的数值模型采用Lourenco和Rots的CIM[9,10]，相关力学参数列于表1中。

表1 砌体剪力墙的力学参数

试验中，剪力墙的最后破坏形态及裂缝分布见图3，Lourenco和Rots的CIM模拟剪力墙的加载破坏最终形态及应力云图如图4。基于AHM的有限元模型在裂缝贯通破坏时的第三主应力云图如图5，第三主应变云图如图6。本例针对计算结果分析如下：

(1)AHM的第三主应力值介于-11.91～+0.57 MPa，CIM为-12.82～+0.90 MPa，在数值上吻合。

(2)AHM有一条大致呈60°的斜向压应力带，而CIM有两条压应力带，分布在斜向裂口两边，在走向上大致吻合。CIM有两条压应力带的原因是该模型在加载后期砖和砂浆发生断裂产生裂口之后内应力重新分布。

(3)AHM和CIM两个模型的两个趾部压应力水平都很高，并最终导致趾部压溃，局部应力分布与试验和CIM相似。

(4)AHM模拟得到的顶部最大水平位移d=3.05 mm，而CIM模拟得到的剪力墙破坏时的最大位移d=4.0 mm，误差为23.75%。这是因为AHM在弹性范围内分析，而CIM考虑了断裂和损伤，所以AHM模拟得到的水平位移相对较小。

(5)AHM的应变云图表明有一条大致呈60°的斜向压应变带，在这条压应变带中将先产生裂缝，因为AHM没有考虑断裂和损伤，所以图中没有裂缝。而剪力墙试验和CIM表明在加载的早期底部和顶部就产生了水平拉裂裂缝，加载后期产生形似踏步的斜向裂缝，随着趾部砖被压溃和中部斜裂缝处砖的突然断裂使斜裂缝贯通，最终导致了剪力墙的破坏。破坏机理与试验和CIM大致相似。

图4 CIM破坏形态及应力云图

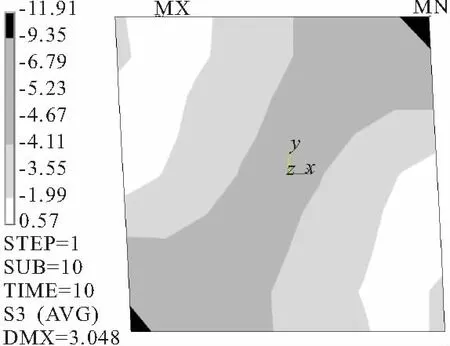
图5 AHM第三主应力云图

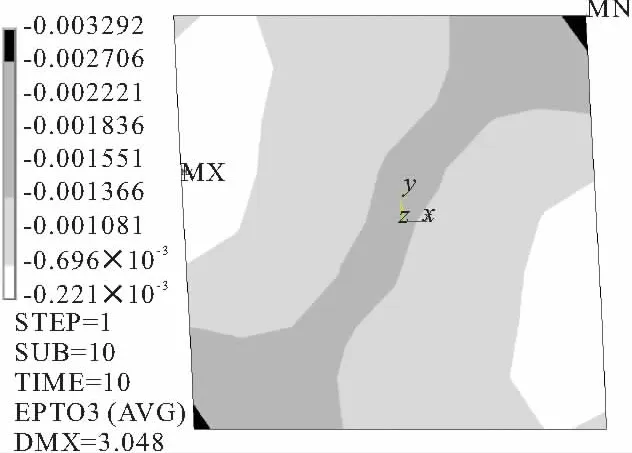
图6 AHM第三主应变云图

3 结论与展望

本文验证了AHM对于砌体三维等效模量的计算是适用的，并应用AHM分析了砌体剪力墙的应力应变状态和破坏机理，得到验证，对砌体结构的设计理论有一定指导意义。对砌体结构进行均匀化处理以后，在ANSYS平台上可以方便的求解出该工况下砌体的等效模量分量，计算精度可以满足工程应用的要求，实现了与工程应用的紧密联系。

今后的工作是发展在ANSYS平台上有效的、便于操作的砌体计算模块，最终与工程应用无缝对接。考虑弹塑性和损伤的砌体极限状态分析，进一步分析砌体的破坏机理，为设计方法的发展提供参考。

[1] Hassani B, Hinton E. A review of homogenization and topology optimization I—homogenization theory for media with periodic structure[J]. Computers & Structures, 1998， 69(6):707-717.

[2] Hassani B, Hinton E. A review of homogenization and topology opimization II—analytical and numerical solution of homogenization equations[J]. Computers & Structures, 1998， 69(6):719-738.

[3] Yuan Z, Fish J. Toward realization of computational homogenization in practice[J]. International Journal for Numerical Methods in Engineering, 2008，73(3):361-380.

[4] Zucchini A, Lourenco P B. A micro-mechanical model for the homogenisation of masonry[J]. International Journal of Solids and Structures, 2002, 39(12): 3233-3255.

[5] 印长俊. 周期性复合材料等效模量计算软件:中国, 2012SR113371[P].2012-09-19.

[6] Guedes J, Kikuchi N. Preprocessing and postprocessing for materials based on the homogenization method with adaptive finite element methods[J]. Computer Methods in Applied Mechanics and Engineering, 1990, 83(2): 143-198.

[7] Zucchini A, Lourenco P B. A micro-mechanical homogenisation model for masonry: Application to shear walls[J]. International Journal of Solids and Structures, 2009, 46(3-4): 871-886.

[8] CUR. Structural Masonry: An Experimental/Numerical Basis for Practical Design Rules[S]. Balkema Rotterdam: Rots J G (Ed.). 1997.

[9] Lourenco P B, Rots J G. Multisurface interface model for the analysis of masonry structures[J]. Journal of Engineering Mechanics, 1997，(123): 660-668.

[10] Lourenco P B. Computational Strategies for Masonry Structures[D]. Delft: Delft University of Technology, 1996.